Exercícios para o ENEM (484)

Gregor Mendel, no século XIX, investigou os mecanismos da herança genética observando algumas características de plantas de ervilha, como a produção de sementes lisas (dominante) ou rugosas (recessiva), característica determinada por um par de alelos com dominância completa. Ele acreditava que a herança era transmitida por fatores que, mesmo não percebidos nas características visíveis (fenótipo) de plantas híbridas (resultantes de cruzamentos de linhagens puras), estariam presentes e se manifestariam em gerações futuras.

A autofecundação que fornece dados para corroborar a ideia da transmissão dos fatores idealizada por Mendel ocorre entre plantas

Uma empresa de comunicação tem a tarefa de elaborar um material publicitário de um estaleiro para divulgar um novo navio, equipado com um guindaste de 15 m de altura e uma esteira de 90 m de comprimento. No desenho desse navio, a representação do guindaste deve ter sua altura entre 0,5 cm e 1 cm, enquanto a esteira deve apresentar comprimento superior a 4 cm. Todo o desenho deverá ser feito em uma escala 1 : X.

Os valores possíveis para X são, apenas,

Um edifício tem a numeração dos andares iniciando no térreo (T), e continuando com primeiro, segundo, terceiro, ..., até o último andar. Uma criança entrou no elevador e, tocando no painel, seguiu uma sequência de andares, parando, abrindo e fechando a porta em diversos andares. A partir de onde entrou a criança, o elevador subiu sete andares, em seguida desceu dez, desceu mais treze, subiu nove, desceu quatro e parou no quinto andar, finalizando a sequência. Considere que, no trajeto seguido pela criança, o elevador parou uma vez no último andar do edifício.

De acordo com as informações dadas, o último andar do edifício é o

O Salão do Automóvel de São Paulo é um evento no qual vários fabricantes expõem seus modelos mais recentes de veículos, mostrando, principalmente, suas inovações em design e tecnologia.

Disponível em: http://g1.globo.com. Acesso em: 4 fev. 2015 (adaptado).

Uma montadora pretende participar desse evento com dois estandes, um na entrada e outro na região central do salão, expondo, em cada um deles, um carro compacto e uma caminhonete.

Para compor os estandes, foram disponibilizados pela montadora quatro carros compactos, de modelos distintos, e seis caminhonetes de diferentes cores para serem escolhidos aqueles que serão expostos. A posição dos carros dentro de cada estande é irrelevante.

Uma expressão que fornece a quantidade de maneiras diferentes que os estandes podem ser compostos é

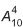
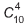
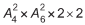
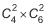
Os alunos da disciplina de estatística, em um curso universitário, realizam quatro avaliações por semestre com os pesos de 20%, 10%, 30% e 40%, respectivamente. No final do semestre, precisam obter uma média nas quatro avaliações de, no mínimo, 60 pontos para serem aprovados. Um estudante dessa disciplina obteve os seguintes pontos nas três primeiras avaliações: 46, 60 e 50, respectivamente.

O mínimo de pontos que esse estudante precisa obter na quarta avaliação para ser aprovado é

Um produtor de milho utiliza uma área de 160 hectares para as suas atividades agrícolas. Essa área é dividida em duas partes: uma de 40 hectares, com maior produtividade, e outra, de 120 hectares, com menor produtividade. A produtividade é dada pela razão entre a produção, em tonelada, e a área cultivada. Sabe-se que a área de 40 hectares tem produtividade igual a 2,5 vezes à da outra. Esse fazendeiro pretende aumentar sua produção total em 15%, aumentando o tamanho da sua propriedade. Para tanto, pretende comprar uma parte de uma fazenda vizinha, que possui a mesma produtividade da parte de 120 hectares de suas terras.

Qual é a área mínima, em hectare, que o produtor precisará comprar?

Torneios de tênis, em geral, são disputados em sistema de eliminatória simples. Nesse sistema, são disputadas partidas entre dois competidores, com a eliminação do perdedor e promoção do vencedor para a fase seguinte. Dessa forma, se na 1ª fase o torneio conta com 2n competidores, então na 2ª fase restarão n competidores, e assim sucessivamente até a partida final.

Em um torneio de tênis, disputado nesse sistema, participam 128 tenistas.

Para se definir o campeão desse torneio, o número de partidas necessárias é dado por

Para apagar os focos A e B de um incêndio, que estavam a uma distância de 30 m um do outro, os bombeiros de um quartel decidiram se posicionar de modo que a distância de um bombeiro ao foco A, de temperatura mais elevada, fosse sempre o dobro da distância desse bombeiro ao foco B, de temperatura menos elevada.

Nestas condições, a maior distância, em metro, que dois bombeiros poderiam ter entre eles é

Um rapaz estuda em uma escola que fica longe de sua casa, e por isso precisa utilizar o transporte público. Como é muito observador, todos os dias ele anota a hora exata (sem considerar os segundos) em que o ônibus passa pelo ponto de espera. Também notou que nunca consegue chegar ao ponto de ônibus antes de 6 h 15 min da manhã. Analisando os dados coletados durante o mês de fevereiro, o qual teve 21 dias letivos, ele concluiu que 6 h 21 min foi o que mais se repetiu, e que a mediana do conjunto de dados é 6 h 22 min.

A probabilidade de que, em algum dos dias letivos de fevereiro, esse rapaz tenha apanhado o ônibus antes de 6 h 21 min da manhã é, no máximo,

Para ganhar um prêmio, uma pessoa deverá retirar, sucessivamente e sem reposição, duas bolas pretas de uma mesma urna. Inicialmente, as quantidades e cores das bolas são como descritas a seguir:

• Urna A - Possui três bolas brancas, duas bolas pretas e uma bola verde;

• Urna B - Possui seis bolas brancas, três bolas pretas e uma bola verde;

• Urna C - Possui duas bolas pretas e duas bolas verdes;

• Urna D - Possui três bolas brancas e três bolas pretas.

A pessoa deve escolher uma entre as cinco opções apresentadas:

• Opção 1 - Retirar, aleatoriamente, duas bolas da urna A;

• Opção 2 - Retirar, aleatoriamente, duas bolas da urna B;

• Opção 3 - Passar, aleatoriamente, uma bola da urna C para a urna A; após isso, retirar, aleatoriamente, duas bolas da urna A;

• Opção 4 - Passar, aleatoriamente, uma bola da urna D para a urna C; após isso, retirar, aleatoriamente, duas bolas da urna C;

• Opção 5 - Passar, aleatoriamente, uma bola da urna C para a urna D; após isso, retirar, aleatoriamente, duas bolas da urna D.

Com o objetivo de obter a maior probabilidade possível de ganhar o prêmio, a pessoa deve escolher a opção