Lentes Esféricas

As lentes esféricas fazem parte do estudo da física óptica, sendo um dispositivo óptico composto por três meios homogêneos e transparentes.

Nesse sistema, dois dioptros estão associados, sendo que um deles é necessariamente esférico. Já o outro dioptro, pode ser plano ou esférico.

As lentes possuem uma grande importância nas nossas vidas, posto que com elas podemos aumentar ou reduzir o tamanho de um objeto.

Exemplos

Muito objetos do cotidiano utilizam as lentes esféricas, por exemplo:

• Óculos
• Lupa
• Microscópios
• Telescópios
• Câmeras Fotográficas
• Filmadoras
• Projetores

Tipos de Lentes Esféricas

De acordo com a curvatura que apresentam, as lentes esféricas são classificadas em dois tipos:

Lentes Convergentes

Também chamadas de lentes convexas, as lentes convergentes apresentam uma curvatura para o exterior. O centro é mais espesso e a borda é mais delgada.

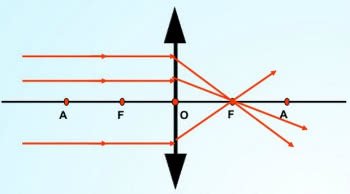
Esquema de lente convergente

O principal objetivo desse tipo de lente esférica é de aumentar os objetos. Recebem esse nome pois os raios de luz convergem, ou seja, se aproximam.

Lentes Divergentes

Também chamadas de lentes côncavas, as lentes divergentes apresentam uma curvatura interna. O centro é mais fino e a borda é mais espessa.

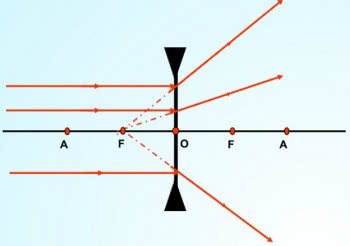
Esquema de lente divergente

O principal objetivo desse tipo de lente esférica é de diminuir os objetos. Recebem esse nome pois os raios de luz divergem, ou seja, afastam.

Além disso, segundo os tipos de dioptros que apresentam (esféricos ou esférico e plano), as lentes esféricas podem ser de seis tipos:

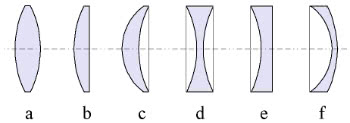
Tipos de Lentes Esféricas

Lentes Convergentes

• a) Biconvexa: possui duas faces convexas
• b) Plano Convexa: uma face é plana, e o outra, convexa
• c) Côncavo-convexa: uma face é côncava, e o outra, convexa

Lentes Divergentes

• d) Bicôncava: possui duas faces côncavas
• e) Plano Côncava: uma face é plana, e a outra, côncava
• f) Convexa-Côncava: uma face é convexa, e a outra, côncava

Obs: Dentre esses tipos, três delas apresentam uma borda mais fina, e três bordas mais espessas.

Aprenda mais sobre lentes convergentes e divergentes.

Quer saber mais sobre o tema? Leia também:

• Reflexão da Luz
• Refração da Luz
• Espelhos Planos
• Espelhos Esféricos
• Luz: Refração, Reflexão e Meios de Propagação
• Fórmulas de Física

Formação de Imagens

A formação de imagens varia de acordo com o tipo de lente:

Lente Convergente

As imagens podem ser formadas em cinco casos:

• Imagem real, invertida e menor do que o objeto
• Imagem real, invertida e mesmo tamanho do objeto
• Imagem real, invertida e maior que o objeto
• Imagem imprópria (está no infinito)
• Imagem virtual, a direita do objeto e maior do que ele

Lente divergente

Já a lente divergente, a formação de imagem é sempre: virtual, a direita do objeto e menor do que ele.

Potência Focal

Cada lente apresenta uma potência focal, ou seja, a capacidade de convergir ou divergir os raios de luz. A potência focal é calculada pela fórmula:

P = 1/f

Sendo,

P: potência focal
f: distância focal (da lente ao foco)

No Sistema Internacional, a potência focal é medida em Dioptria (D) e a distância focal em metros (m).

Importante notar que nas lentes convergentes, a distância focal é positiva, por isso também são chamadas de lentes positivas. Já nas lentes divergentes ela é negativa, e portanto, são chamadas de lentes negativas.

Exemplos

1. Qual a potência focal de uma lente convergente de distância focal de 0,10 metros?

P = 1/f
P = 1/0,10
P = 10 D

2. Qual a potência focal de uma lente divergente de distância focal de 0,20 metros?

P = 1/f
P = 1/-0,20
P = - 5 D

Exercícios de Vestibular com Gabarito

1. (CESGRANRIO) Um objeto real é colocado perpendicularmente ao eixo principal de uma lente convergente de distância focal f. Se o objeto está a uma distância 3f da lente, a distância entre o objeto e a imagem conjugada por essa lente é:

a) f/2
b) 3f/2
c) 5f/2
d) 7f/2
e) 9f/2

2. (MACKENZIE) Considerando uma lente biconvexa cujas faces possuem o mesmo raio de curvatura, podemos afirmar que:

a) o raio de curvatura das faces é sempre igual ao dobro da distância focal;
b) o raio de curvatura é sempre igual à metade do recíproco de sua vergência;
c) ela é sempre convergente, qualquer que seja o meio envolvente;
d) ela só é convergente se o índice de refração do meio envolvente for maior que o do material da lente;
e) ela só é convergente se o índice de refração do material da lente for maior que o do meio envolvente.

3. (UFSM-RS) Um objeto está sobre o eixo óptico e a uma distância p de uma lente convergente de distância f. Sendo p maior que f e menor que 2f, pode-se afirmar que a imagem será:

a) virtual e maior que o objeto;
b) virtual e menor que o objeto;
c) real e maior que o objeto;
d) real e menor que o objeto;
e) real e igual ao objeto.