Espelhos esféricos: o que são, os tipos e a formação de imagens

Os espelhos esféricos ou curvos são superfícies refletoras que têm a forma de uma parte de uma esfera.

Diferente dos espelhos normais, que refletem a luz de forma reta, os espelhos esféricos curvam a luz de acordo com sua forma. Eles são usados em várias coisas do dia a dia, como telescópios, câmeras e faróis de carros.

Nos espelhos esféricos os ângulos de incidência e de reflexão são equivalentes, e os raios incidido, refletidos e a reta normal, ao ponto incidido.

Lembre-se que os espelhos são objetos muito utilizados no dia a dia, compostos de vidro transparente e geralmente cobertos por uma película de prata. São classificados em espelhos planos e esféricos (côncavos e convexos).

Tipos de espelhos esféricos

Note que os espelhos esféricos possuem uma face interna e outra externa, a qual respectivamente denominamos de face côncava e face convexa. Diante disso, há dois tipos de espelhos esféricos:

Espelhos côncavos

São espelhos curvados para dentro, como o interior de uma esfera. Eles refletem a luz convergindo-a para um ponto focal. Devido a essa propriedade, são chamados de espelhos convergentes. Nestes espelhos a superfície refletora é a parte interna da calota esférica.

Espelhos convexos

São espelhos curvados para fora, como o exterior de uma esfera. Eles dispersam a luz refletida, fazendo com que pareçam divergir de um ponto atrás do espelho. Por isso, são conhecidos como espelhos divergentes. Nestes espelhos a superfície refletora é a parte externa da calota esférica.

Para saber mais sobre os espelhos, acesse o link: Espelhos Planos.

Elementos dos Espelhos Esféricos

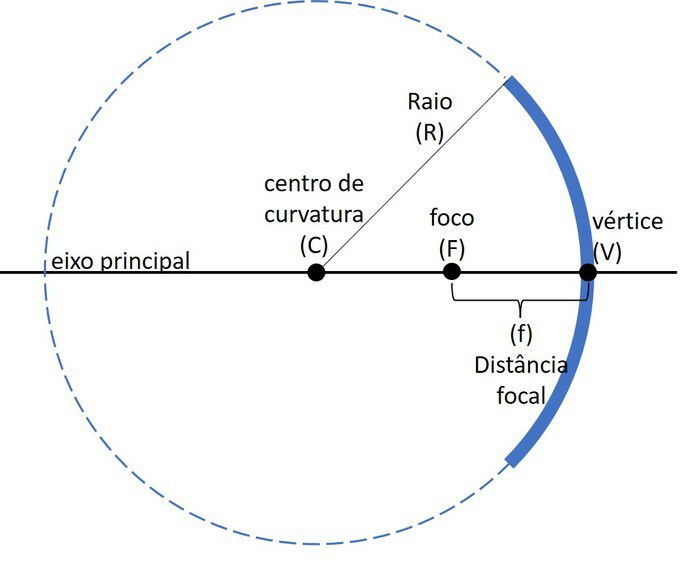
Nos espelhos esféricos, a superfície refletora possui a forma de uma calota esférica, e seus principais elementos são:

Eixo principal: reta que passa pelo centro de curvatura e pelo vértice do espelho;

Centro de Curvatura (C): centro da esfera que originou o espelho. É o centro da esfera da qual o espelho é uma seção;

Vértice (V): É o ponto médio da superfície do espelho (polo da calota);

Raio de Curvatura (R): distância do centro de curvatura até o vértice do espelho. É raio da esfera que originou o espelho;

Foco Principal (F): É o ponto no eixo principal onde os raios paralelos ao eixo principal convergem (espelho côncavo) ou parecem divergir (espelho convexo).

Distância Focal (f): É a distância do vértice ao foco principal, geralmente é igual à metade do raio de curvatura (f = R/2).

Equação dos Espelhos Esféricos

A relação entre a distância do objeto, a distância da imagem e a distância focal de um espelho esférico é dada pela equação do espelho:

Onde:

• p é a distância do objeto ao vértice do espelho;
• q é a distância da imagem ao vértice do espelho;
• f é a distância focal (distância do foco ao vértice).

Exemplo:

Um espelho côncavo possui um raio de curvatura de 40 cm. Um objeto é colocado a 60 cm do vértice do espelho. Utilize a equação dos espelhos esféricos para determinar a posição da imagem formada por este objeto.

Resolução:

Determinar a posição da imagem é conhecer o valor de q na equação.

• Raio de curvatura do espelho (R) = 40 cm
• Distância do objeto ao vértice do espelho (p) = 60 cm

Temos que a distância focal é a metade do raio de curvatura:

Substituindo os valores na equação, temos:

Isolando a razão 1/q de um lado da igualdade:

Multiplicando cruzado para resolver a proporção:

Logo, a imagem está localizada a 30 cm do espelho.

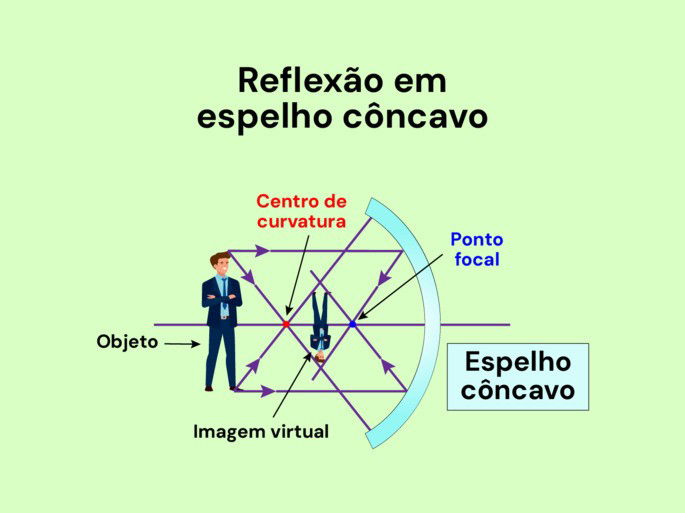
Formação da imagem em espelhos côncavos

No espelho côncavo, dependendo da posição do objeto, a imagem formada pode ser real ou virtual; maior, menor ou igual ao tamanho do objeto; invertida ou direita.

Dessa maneira, se o objeto está localizado sobre o centro de curvatura, a imagem formada será real, invertida e igual ao objeto; se ele se encontra além do centro de curvatura, sua imagem será real, invertida e menor; se o objeto está entre o centro de curvatura e o foco, sua imagem será real, invertida e maior do que o objeto.

No caso de formação de imagem virtual e direita nos espelhos côncavos, o objeto deverá encontrar-se entre o foco e o espelho, constituindo uma imagem maior do que o objeto.

Entretanto, se o objeto estiver localizado sobre o foco, não se formará nenhuma imagem, de forma que os raios luminosos não se cortam.

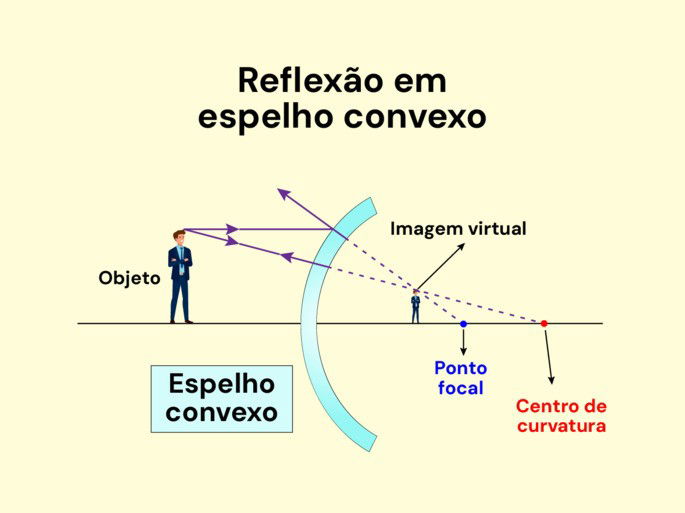
Formação da imagem em espelhos convexos

Já nos espelhos convexos só há um tipo de imagem formada, de modo que apresentará sempre uma imagem virtual, direta e menor do que o objeto, independente da distância que estiver do espelho.

Formação da imagem

Inicialmente vale destacar que as imagens refletidas possuem algumas denominações e características no estudo da física.

Assim, quando dizemos que a imagem refletida no espelho é real, estamos nos referindo à imagem que surge na frente do espelho; quanto a imagem é virtual, ela aparece refletida atrás do espelho.

Outra característica da imagem é se ela aparece direta ou invertida; assim, ela será direta quando o objeto e a imagem possuírem o mesmo sentido (para cima e para baixo); por outro lado, será invertida se os sentidos da imagem e do objeto forem opostos.

Por fim, o objeto pode ter uma imagem refletida igual, maior ou menor, de acordo com seu tamanho real.

Aplicações práticas dos espelhos esféricos

Os espelhos esféricos são empregados em uma variedade de tecnologias devido à sua capacidade única de manipular a luz. Seja concentrando raios de luz ou dispersando-os, esses espelhos têm papel fundamental em equipamentos que vão desde instrumentos científicos até dispositivos de segurança.

Cada tipo de espelho, seja côncavo ou convexo, tem usos específicos que exploram suas propriedades ópticas de maneiras que melhoram a funcionalidade dos dispositivos nos quais são utilizados.

• Telescópios: Em telescópios, os espelhos côncavos são essenciais para coletar luz de fontes distantes, como estrelas e galáxias, e focá-la em um ponto onde possa ser analisada ou visualizada. Por convergir a luz, esses espelhos permitem observações detalhadas de objetos celestes que estão a bilhões de anos-luz de distância.

• Faróis de Automóveis: Nos veículos, os faróis contam com espelhos côncavos para projetar um feixe de luz forte e direcionado à frente. Este uso é crucial para a segurança na condução noturna, ao maximizar a visibilidade sem necessidade de componentes eletrônicos complexos.

• Câmeras de Vigilância: As câmeras de segurança frequentemente incorporam espelhos convexos para oferecer um campo de visão mais amplo. Isso permite que uma única câmera monitore um grande espaço, como lojas, estacionamentos ou outros ambientes públicos, assegurando uma vigilância eficaz com menos equipamentos.

Essas aplicações demonstram como os espelhos esféricos são vitais em diversas áreas, contribuindo para avanços em segurança, transporte e pesquisa científica.

Para saber mais sobre o fenômeno da reflexão: Reflexão da Luz.

Leia também sobre as Lentes Esféricas.

Para mais exercícios de Física:

• Exercícios sobre óptica geométrica
• Exercícios sobre espelhos esféricos
• Exercícios de Física (resolvidos) para 2º ano do ensino médio