Exercícios para o ENEM (152)

Nas empresas em geral, são utilizados dois tipos de copos plásticos descartáveis, ambos com a forma de troncos de cones circulares retos:

• copos pequenos, para a ingestão de café: raios das bases iguais a 2,4 cm e 1,8 cm e altura igual a 3,6 cm;

• copos grandes, para a ingestão de água: raios das bases iguais a 3,6 cm e 2,4 cm e altura igual a 8,0 cm.

Uma dessas empresas resolve substituir os dois modelos de copos descartáveis, fornecendo para cada um de seus funcionários canecas com a forma de um cilindro circular reto de altura igual a 6 cm e raio da base de comprimento igual a y centímetros. Tais canecas serão usadas tanto para beber café como para beber água.

Sabe-se que o volume de um tronco de cone circular reto, cujos raios das bases são respectivamente iguais a R e r e a altura é h, é dado pela expressão:

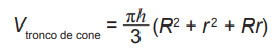
O raio y da base dessas canecas deve ser tal que y² seja, no mínimo, igual a

Durante seu treinamento, um atleta percorre metade de uma pista circular de raio R, conforme figura a seguir. A sua largada foi dada na posição representada pela letra L, a chegada está representada pela letra C e a letra A representa o atleta. O segmento LC é um diâmetro da circunferência e o centro da circunferência está representado pela letra F.

Sabemos que, em qualquer posição que o atleta esteja na pista, os segmentos LA e AC são perpendiculares. Seja θ o ângulo que o segmento AF faz com segmento FC.

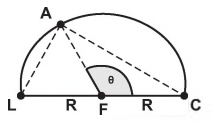
Quantos graus mede o ângulo θ quando o segmento AC medir R durante a corrida?

Uma prefeitura possui modelos de lixeira de forma cilíndrica, sem tampa, com raio medindo 10 cm e altura de 50 cm. Para fazer uma compra adicional, solicita à empresa fabricante um orçamento de novas lixeiras, com a mesma forma e outras dimensões. A prefeitura só irá adquirir as novas lixeiras se a capacidade de cada uma for no mínimo dez vezes maior que o modelo atual e seu custo unitário não ultrapassar R$ 20,00. O custo de cada lixeira é proporcional à sua área total e o preço do material utilizado na sua fabricação é de R$ 0,20 para cada 100 cm2. A empresa apresenta um orçamento discriminando o custo unitário e as dimensões, com o raio sendo o triplo do anterior e a altura aumentada em 10 cm. (Aproxime π para 3.)

O orçamento dessa empresa é rejeitado pela prefeitura, pois

Vítor deseja revestir uma sala retangular de dimensões 3 m x 4 m, usando um tipo de peça de cerâmica. Em uma pesquisa inicial, ele selecionou cinco tipos de peças disponíveis, nos seguintes formatos e dimensões:

• Tipo I: quadrados, com 0,5 m de lado.

• Tipo II: triângulos equiláteros, com 0,5 m de lado.

• Tipo III: retângulos, com dimensões 0,5 m x 0,6 m.

• Tipo IV: triângulos retângulos isósceles, cujos catetos medem 0,5 m.

• Tipo V: quadrados, com 0,6 m de lado.

Analisando a pesquisa, o mestre de obras recomendou que Vítor escolhesse um tipo de piso que possibilitasse a utilização do menor número de peças e não acarretasse sobreposições ou cortes nas cerâmicas.

Qual o tipo de piso o mestre de obras recomendou que fosse comprado?

Um jovem lança uma bola de borracha para observar sua trajetória e altura h (em metros) atingida ao longo de um certo intervalo de tempo t (em segundos). Nesse intervalo, a bola quica no chão algumas vezes, perdendo altura progressivamente. Parte de sua trajetória está descrita na figura a seguir.

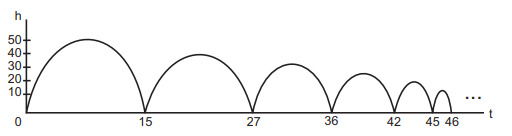
Em suas observações, quantas vezes o jovem pôde constatar que a bola atingiu a marca de 35 metros?

Uma pizzaria oferece, no cardápio, duas opções de tamanhos e preços:

Pizza média (6 fatias): R$ 24,00

Pizza grande (8 fatias): R$ 32,00

Um grupo de jovens estava prestes a decidir o tipo de pizza com melhor custo-benefício, quando um dos amigos questionou ao garçom a respeito do diâmetro de cada uma das pizzas. A informação obtida foi de que os diâmetros das pizzas média e grande eram, respectivamente, 30 cm e 40 cm. Considerando que os dois tamanhos e preços das pizzas atendem o grupo e que não haverá desperdício, iniciou-se um debate entre eles:

• Alan: A pizza grande tem melhor custo-benefício, pois a área de sua fatia é superior à área da fatia da pizza média.

• Breno: A pizza média tem melhor custo-benefício, pois, como é dividida em menos fatias, cada fatia tem uma maior quantidade de pizza.

• Cleber: As duas apresentam a mesma relação custo-benefício, já que cada fatia custa R$ 4,00, independentemente da escolha do tamanho.

• Davidson: Como a razão entre os diâmetros e os preços das pizzas é a mesma, nenhuma das pizzas tem melhor custo-benefício que a outra.

• Eric: A pizza grande possui melhor relação custo/benefício, pois, independentemente do diâmetro, ela é dividida em um número maior de fatias.

Qual jovem apresentou o melhor argumento para a escolha da pizza?

Um jornaleiro irá receber 21 revistas. Cada uma terá um carrinho na escala de 1:43 do tamanho real acompanhando-a em caixinha à parte. Os carrinhos são embalados com folga de 0,5 cm nas laterais, como indicado na figura. Assim, o jornaleiro reservou três prateleiras com 95 cm de comprimento por 7 cm de largura, onde as caixas serão acomodadas de forma a caberem inteiramente dentro de cada prateleira. Além disso, sabe-se que os carrinhos são cópias dos modelos reais que possuem 387 cm de comprimento por 172 cm de largura.

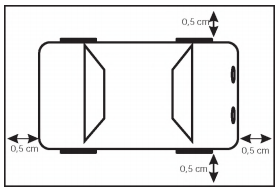
Quantos carrinhos, no máximo, cabem em cada uma das prateleiras?

Em um terreno, deseja-se instalar uma piscina com formato de um bloco retangular de altura 1 m e base de dimensões 20 m x 10 m. Nas faces laterais e no fundo desta piscina será aplicado um líquido para a impermeabilização. Esse líquido deve ser aplicado na razão de 1 L para cada 1 m2 de área a ser impermeabilizada. O fornecedor A vende cada lata de impermeabilizante de 10 L por R$ 100,00, e o B vende cada lata de 15 L por R$ 145,00.

Determine a quantidade de latas de impermeabilizante que deve ser comprada e o fornecedor a ser escolhido, de modo a se obter o menor custo.

O Índice de Desenvolvimento Humano (IDH) mede a qualidade de vida dos países para além dos indicadores econômicos. O IDH do Brasil tem crescido ano a ano e atingiu os seguintes patamares: 0,600 em 1990; 0,665 em 2000; 0,715 em 2010. Quanto mais perto de 1,00, maior é o desenvolvimento do país.

O Globo. Caderno Economia, 3 nov. 2011 (adaptado).

Observando o comportamento do IDH nos períodos citados, constata-se que, ao longo do período 1990-2010, o IDH brasileiro

— É o diabo!... praguejava entre dentes o brutalhão, enquanto atravessava o corredor ao lado do Conselheiro, enfiando às pressas o seu inseparável sobretudo de casimira alvadia. — É o diabo! Esta menina já devia ter casado!

— Disso sei eu... balbuciou o outro. — E não é por falta de esforços de minha parte; creia!

— Diabo! Faz lástima que um organismo tão rico e tão bom para procriar, se sacrifique desse modo! Enfim — ainda não é tarde; mas, se ela não se casar quanto antes — hum... hum!... Não respondo pelo resto!

— Então o Doutor acha que...?

Lobão inflamou-se: Oh! o Conselheiro não podia imaginar o que eram aqueles temperamentozinhos impressionáveis!... eram terríveis, eram violentos, quando alguém tentava contrariá-los! Não pediam — exigiam — reclamavam!

AZEVEDO, A. O homem. Belo Horizonte: UFMG, 2003 (fragmento).

O romance O homem, de Aluísio Azevedo, insere-se no contexto do Naturalismo, marcado pela visão do cientificismo. No fragmento, essa concepção aplicada à mulher define-se por uma