Números complexos: entenda o que são e suas operações (com exercícios)

Os números complexos são números compostos por uma parte real e uma imaginária.

Eles representam o conjunto de todos os pares ordenados (x, y), cujos elementos pertencem ao conjunto dos números reais (R).

O conjunto dos números complexos é indicado por , onde se definem as operações:

• Igualdade: (a, b) = (c, d) ↔ a = c e b = d
• Adição: (a, b) + (c, d) = (a + c, b + d)
• Multiplicação: (a, b) . (c, d) = (ac – bd, ad + bc)

Neste conteúdo você vai encontrar:

• Estrutura dos números complexos
• Igualdade entre números complexos
• Operações com números complexos
• Conjugado de um número complexo
• Plano complexo ou plano de Argand-Gauss
• Exercícios sobre números complexos com Gabarito
• Mapa Mental

Estrutura dos números complexos

Um número complexo é geralmente escrito na forma algébrica como:

Aqui, a e b são números reais.

• a é a parte real do número complexo.
• bi é a parte imaginária, onde i é a unidade imaginária, a raiz quadrada de -1 ().

Por exemplo, no número complexo 3 + 4i

• 3 é a parte real.
• 4i é a parte imaginária.

Outros exemplos:

• z = 4 + 3i, onde 4 é a parte real e 3i a imaginária
• z = 8, onde 8 é a parte real e 0 a imaginária
• z = 16i, onde 0 é a parte real e 16i a imaginária. (neste caso z é um imaginário puro)

Unidade imaginária (i)

Indicado pela letra i, a unidade imaginária é o par ordenado (0, 1). Logo:

Assim, i é a raiz quadrada de –1, pois:

Exemplo

Igualdade entre números complexos

Sendo dois números complexos Z₁ = (a, b) e Z₂ = (c, d), eles são iguais quando a = c e b = d. Isso porque eles possuem partes reais e imaginárias idênticas. Assim:

a + bi = c + di quando a = c e b = d

Exemplo

e

Então =

Operações com números complexos

Com os números complexos é possível realizar as operações de adição, subtração, multiplicação e divisão. Confira as definições e exemplos:

Adição

Para somar dois números complexos, você adiciona suas partes reais e suas partes imaginárias separadamente.

Z₁ + Z₂

Se você tem z1 = a + bi e z2 = c + di

z1 + z2 = (a + c) + (b + d)i

Exemplo

(3 + 2i) + (1 + 4i) = (3 + 1) + (2 + 4)i = 4 + 6i

Subtração

A subtração de números complexos é feita como a da adição. Subtraímos as partes reais e imaginárias de cada complexo.

Sendo z1 = (a+bi) e z2 = (c+di), a subtração é definida como:

Z₁ – Z_{2 =} (a + bi) – (c + di) = (a – c) + i(b – d)

Exemplo
Subtraia os números complexos z1 = (4 - 5i) e z2 = (2 + i).

Z₁ – Z_{2 =}
(4 – 5i) – (2 + i)
(4 – 2) + i (–5 –1)
2 – 6i

Multiplicação

Para multiplicar números complexos utilizamos a propriedade distributiva. Cada termo de um número complexo multiplica os dois termos do outro.

Após as multiplicações, reduzimos os termos semelhantes realizando somas ou subtrações. Parte real com parte real e imaginária com imaginária.

Como um dos produtos será i², devemos substituí-lo por -1.
Z₁ . Z_{2 =} (a + bi) . (c + di)

Multiplicando os termos:
ac + adi + bci + bdi² =

Substituindo i²
ac + adi + bci + bd . (-1) =
ac + adi + bci - bd

Juntando as partes reais e imaginárias:
(ac – bd) + i(ad + bc)

Exemplo
(4 + 3i) . (2 – 5i)
8 – 20i + 6i – 15i²
8 – 14i + 15
23 – 14i

Divisão

Para dividir dois números complexos, multiplicamos o numerador e o denominador pelo mesmo número complexo do denominador. No entanto, o sinal de sua parte imaginária deve ser trocado.

Se z1 = a + bi e z2 = c + di, a divisão é definida como:

Exemplo

Sendo z1 = 3 + 4i e z2 = 5 + 6i, determine z1 / z2.

Multiplicando os termos:

Simplificando os termos semelhantes e substituindo i² por -1:

Conjugado de um número complexo

O conjugado de um número complexo z = a + bi é definido por:

Assim, troca-se o sinal de sua parte imaginária.

Exemplos

Se z = 5 + 2i, então

Se z = 1 - 3i, então

Se z = -15i, então

Se z = 4. então

Quando multiplicamos um número complexo por seu conjugado, o resultado será um número real.

Plano complexo ou plano de Argand-Gauss

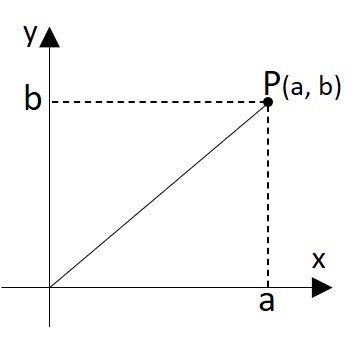
Os números complexos podem ser representados geometricamente no plano complexo.

Dado um número complexo em sua forma algébrica, z = a + bi, um ponto P no plano complexo tem as coordenadas P(a, b) representa este número complexo.

Módulo de um número complexo

O módulo ou, medida de comprimento, de um número complexo é a distância entre a origem do sistema de coordenadas e o ponto que o define no plano complexo. É representado por entre barras verticais, |z| ou pela letra grega e definido como:

Esta definição vem do teorema de Pitágoras, aplicado no triângulo retângulo OPa. |z| é a hipotenusa do triângulo.

Exercícios sobre números complexos resolvidos

Exercicio 1

(UF-TO) Considere i a unidade imaginária dos números complexos. O valor a expressão (i + 1)⁸ é:

a) 32i
b) 32
c) 16
d) 16i

Exercício 2

(UEL-PR) O número complexo z que verifica a equação iz – 2w + (1 + i) = 0 (w indica o conjugado de z) é:

a) z = 1 + i
b) z = (1/3) – i
c) z = (1 – i)/3
d) z = 1 + (i/3)
e) z = 1 – i

Exercício 3

(Vunesp-SP) Considere o número complexo z = cos π/6 + i sen π/6. O valor de Z³ + Z⁶ + Z¹² é:

a) – i
b) ½ +√3/2i
c) i – 2
d) i
e) 2i

Confira mais questões com resolução comentada, em Exercícios sobre Números Complexos.

Mapa mental sobre números complexos

História dos números complexos

A descoberta dos números complexos foi realizada no século XVI graças as contribuições do matemático Girolamo Cardano (1501-1576).

No entanto, somente no século XVIII que esses estudos foram formalizados pelo matemático Carl Friedrich Gauss (1777-1855).

Os números complexos foram um avanço na matemática, visto um número negativo ter uma raiz com índice par, o que até a descoberta dos números complexos era considerado impossível.