Polinômios

Rosimar Gouveia

Professora de Matemática e Física

Os polinômios são expressões algébricas formadas por números (coeficientes) e letras (partes literais). As letras de um polinômio representam os valores desconhecidos da expressão.

Exemplos

a) 3ab + 5
b) x³ + 4xy - 2x²y³
c) 25x² - 9y²

Monômio, Binômino e Trinômio

Os polinômios são formados por termos. A única operação entre os elementos de um termo é a multiplicação.

Quando um polinômio possui apenas um termo, ele é chamado de monômio.

Exemplos

a) 3x
b) 5abc
c) x²y³z⁴

Os chamados binômios são polinômios que possuem somente dois monômios (dois termos), separados por uma operação de soma ou subtração.

Exemplos

a) a² - b²
b) 3x + y
c) 5ab + 3cd²

Já os trinômios são polinômios que possuem três monômios (três termos), separados por operações de soma ou subtração.

Exemplos

a) x² + 3x + 7
b) 3ab - 4xy - 10y
c) m³n + m² + n⁴

Grau dos Polinômios

O grau de um polinômio é dado pelos expoentes da parte literal.

Para encontrar o grau de um polinômio devemos somar os expoentes das letras que compõem cada termo. A maior soma será o grau do polinômio.

Exemplos

a) 2x³ + y

O expoente do primeiro termo é 3 e do segundo termo é 1. Como o maior é 3, o grau do polinômio é 3.

b) 4 x²y + 8x³y³ - xy⁴

Vamos somar os expoentes de cada termo:

4x²y => 2 + 1 = 3
8x³y³ => 3 + 3 = 6
xy⁴ => 1 + 4 = 5

Como a maior soma é 6, o grau do polinômio é 6

Obs: o polinômio nulo é aquele que possui todos os coeficientes iguais a zero. Quando isso ocorre, o grau do polinômio não é definido.

Operações com Polinômios

Confira abaixo exemplos das operações entre polinômios:

Adição de Polinômios

Fazemos essa operação somando os coeficientes dos termos semelhantes (mesma parte literal).

(- 7x³ + 5 x²y - xy + 4y) + (- 2x²y + 8xy - 7y)
- 7x³ + 5x²y - 2x²y - xy + 8xy + 4y - 7y
- 7x³ + 3x²y + 7xy - 3y

Subtração de Polinômios

O sinal de menos na frente dos parênteses inverte os sinais de dentro dos parênteses. Após eliminar os parênteses, devemos juntar os termos semelhantes.

(4x² - 5xk + 6k) - (3xk - 8k)
4x² - 5xk + 6k - 3xk + 8k
4x² - 8xk + 14k

Multiplicação de Polinômios

Na multiplicação devemos multiplicar termo a termo. Na multiplicação de letras iguais, repete-se e soma-se os expoentes.

(3x² - 5x + 8) . (-2x + 1)
-6x³ + 3x² + 10x² - 5x - 16x + 8
-6x³ + 13x² - 21x +8

Divisão de Polinômios

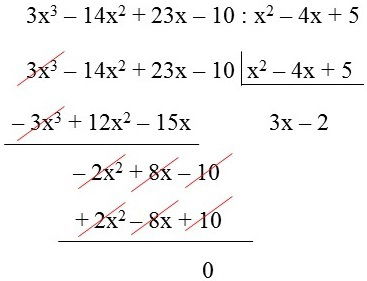
Obs: Na divisão de polinômios utilizamos o método chave. Primeiramente realizamos a divisão entre os coeficientes numéricos e depois a divisão de potências de mesma base. Para isso, conserva-se a base e subtraia os expoentes.

Fatoração de Polinômios

Para realizar a fatoração de polinômios temos os seguintes casos:

Fator Comum em Evidência

ax + bx = x (a + b)

Exemplo

4x + 20 = 4 (x + 5)

Agrupamento

ax + bx + ay + by = x . (a + b) + y . (a + b) = (x + y) . (a + b)

Exemplo

8ax + bx + 8ay + by = x (8a + b) + y (8a + b) = (8a + b) . (x + y)

Trinômio Quadrado Perfeito (Adição)

a² + 2ab + b² = (a + b)²

Exemplo

x² + 6x + 9 = (x + 3)²

Trinômio Quadrado Perfeito (Diferença)

a² - 2ab + b² = (a - b)²

Exemplo

x² - 2x + 1 = (x - 1)²

Diferença de Dois Quadrados

(a + b) . (a - b) = a² - b²

Exemplo

x² - 25 = (x + 5) . (x - 5)

Cubo Perfeito (Adição)

a³ + 3a²b + 3ab² + b³ = (a + b)³

Exemplo

x³ + 6x² + 12x + 8 = x³ + 3 . x² . 2 + 3 . x . 2² + 2³ = (x + 2)³

Cubo Perfeito (Diferença)

a³ - 3a²b + 3ab² - b³ = (a - b)³

Exemplo

y³ - 9y² + 27y - 27 = y³ - 3 . y² . 3 + 3 . y . 3² - 3³ = (y - 3)³

Leia também:

• Produtos Notáveis
• Produtos Notáveis - Exercícios
• Função Polinomial

Exercícios Resolvidos

1) Classifique em monômios, binômios e trinômios, os polinômios abaixo:

a) 3abcd²
b) 3a + bc - d²
c) 3ab - cd²

2) Indique o grau dos polinômios:

a) xy³ + 8xy + x²y
b) 2x⁴ + 3
c) ab + 2b + a
d) zk⁷ - 10z²k³w⁶ + 2x

3) Qual o valor do perímetro da figura abaixo:

4) Encontre a área da figura:

5) Fatore os polinômios

a) 8ab + 2a²b - 4ab²
b) 25 + 10y + y²
c) 9 - k²

Veja também:

• Expressões Algébricas
• Exercícios sobre Expressões Algébricas
• Exercícios de fatoração de polinômios resolvidos

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.