Sistemas de Equações

Um sistema de equações é constituído por um conjunto de equações que apresentam mais de uma incógnita. Para resolver um sistema é necessário encontrar os valores que satisfaçam simultaneamente todas as equações.

Um sistema é chamado do 1º grau, quando o maior expoente das incógnitas, que integram as equações, é igual a 1 e não existe multiplicação entre essas incógnitas.

Como resolver um sistema de equações do 1º grau?

Podemos resolver um sistema de equações do 1º grau, com duas incógnitas, usando o método da substituição ou o da soma.

Método da substituição

Esse método consiste em escolher uma das equações e isolarmos uma das incógnitas, para determinar o seu valor em relação a outra incógnita. Depois, substituímos esse valor na outra equação.

Desta forma, a segunda equação ficará com uma única incógnita e, assim, poderemos encontrar o seu valor final. Para finalizar, substituímos na primeira equação o valor encontrado e, assim, encontramos também o valor da outra incógnita.

Exemplo

Resolva o seguinte sistema de equações:

Resolução

Vamos começar escolhendo a primeira equação do sistema, que é a equação mais simples, para isolar o x. Assim temos:

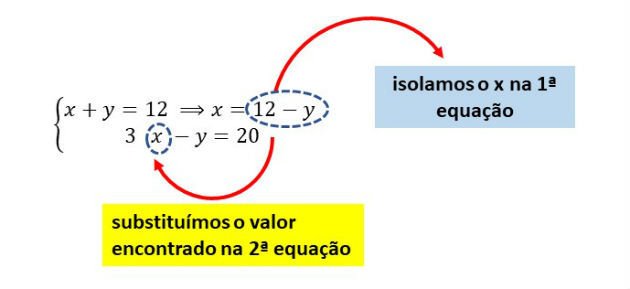
Após substituir o valor de x, na segunda equação, podemos resolvê-la, da seguinte maneira:

Agora que encontramos o valor do y, podemos substituir esse valor da primeira equação, para encontrar o valor do x:

Assim, a solução para o sistema dado é o par ordenado (8, 4). Repare que esse resultado tornam ambas as equações verdadeiras, pois 8 + 4 = 12 e 3.8 - 4 = 20.

Método da Adição

No método da adição buscamos juntar as duas equações em uma única equação, eliminando uma das incógnitas.

Para isso, é necessário que os coeficientes de uma das incógnitas sejam opostos, isto é, devem ter o mesmo valor e sinais contrários.

Exemplo

Para exemplificar o método da adição, vamos resolver o mesmo sistema anterior:

Note que nesse sistema a incógnita y possui coeficientes opostos, ou seja, 1 e - 1. Então, iremos começar a calcular somando as duas equações, conforme indicamos abaixo:

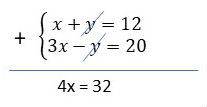
Ao anular o y, a equação ficou apenas com o x, portanto agora, podemos resolver a equação:

Para encontrar o valor do y, basta substituir esse valor em uma das duas equações. Vamos substituir na mais simples:

Note que o resultado é o mesmo que já havíamos encontrado, usando o método da substituição.

Quando as equações de um sistema não apresentam incógnitas com coeficientes opostos, podemos multiplicar todos os termos por um determinado valor, a fim de tornar possível utilizar esse método.

Por exemplo, no sistema abaixo, os coeficientes de x e de y não são opostos:

Portanto, não podemos, inicialmente, anular nenhuma das incógnitas. Neste caso, devemos multiplicar por algum número que transforme o coeficiente em um número oposto do coeficiente da outra equação.

Podemos, por exemplo, multiplicar a primeira equação por - 2. Contudo, devemos ter o cuidado de multiplicarmos todos os termos por - 2, para não modificarmos a igualdade.

Assim, o sistema equivalente ao que queremos calcular é:

Agora, é possível resolver o sistema por adição, conforme apresentado abaixo:

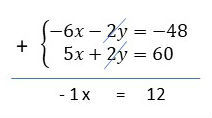
Logo, x = - 12, não podemos esquecer de substituir esse valor em uma das equações para encontrar o valor do y. Substituindo na primeira equação, temos:

Assim, a solução para o sistema é o par ordenado (- 12, 60)

Classificação dos sistemas de equações

Um sistema do 1º grau, com duas incógnitas x e y, formado pelas equações a₁x + b₁y = c₁ e a₂x + b₂y = c₂, terá a seguinte classificação: possível e determinado, possível e indeterminado e impossível.

O sistema será possível e determinado quando apresentar uma única solução. Isso acontecerá quando:

Quando o sistema apresentar infinitas soluções, será classificado como possível e indeterminado. A condição para que um sistema seja desse tipo é:

Já os sistemas impossíveis, não possuem nenhuma solução. Nesse tipo de sistema temos:

Exemplo

Classifique o sistema abaixo:

Para identificar o tipo de sistema, vamos calcular a razão entre os coeficientes das equações:

Como

Então, o sistema é impossível.

Para saber mais, leia também:

• Sistemas de Equações do 1º grau - Exercícios
• Sistemas lineares
• Exercícios de sistemas lineares resolvidos
• Equação do Primeiro Grau
• Equação do Segundo Grau
• Equações irracionais
• Inequação

Exercícios Resolvidos

1) Cefet - RJ - 2016

Uma garrafa PET (politereftalato de etileno) com sua tampa custa sessenta centavos. Sabendo que a garrafa custa cinquenta centavos a mais que a tampa, quanto custa só a tampa?

a) R$ 0,05
b) R$ 0,15
c) R$ 0,25
d) R$ 0,35

2) Cefet - RJ - 2014

Se eu leio 5 páginas por dia de um livro, eu termino de ler 16 dias antes do que se eu estivesse lendo 3 páginas por dia. Quantas páginas tem o livro?

a) 120
b) 125
c) 130
d) 135

3) Uerj - 2015

De acordo com os dados do quadrinho, a personagem gastou R$ 67,00 na compra de x lotes de maçã, y melões e quatro dúzias de bananas, em um total de 89 unidades de frutas.
Desse total, o número de unidades de maçãs comprado foi igual a:

a) 24
b) 30
c) 36
d) 42