Sistemas Lineares

Rafael C. Asth

Professor de Matemática e Física

Sistemas Lineares são conjuntos de equações lineares, associadas entre si, que apresentam como exemplo a forma a seguir:

$abre chaves atributos de tabela alinhamento de coluna left fim dos atributos linha com célula com reto x espaço mais espaço reto y espaço mais espaço reto z espaço igual a espaço 1 espaço fim da célula linha com célula com 2 reto x espaço mais espaço reto y espaço mais espaço 3 reto z espaço igual a espaço 5 fim da célula linha com célula com 5 reto x espaço mais espaço 4 reto y espaço mais espaço 2 reto z espaço igual a espaço 10 fim da célula fim da tabela fecha$

A chave do lado esquerdo é o símbolo usado para sinalizar que as equações fazem parte de um sistema. Estes sistemas podem possuir um número variado de equações e incógnitas.

Os coeficientes são os números que multiplicam as letras, chamadas de incógnitas, que nos sistemas lineares, possuem expoente no máximo igual a 1.

Os números dos coeficientes pertencem ao conjunto dos números reais. Os do lado direto da igualdade são chamados de termos independentes e também números reais.

Nem todo sistema possui solução, quando há, esta solução é dada pelo conjunto de valores (x, y, z ...) que tornam verdadeiras cada equação.

Sistemas lineares homogêneos são aqueles cujos termos independentes são iguais a 0 (zero).

Classificação dos sistemas lineares

Os sistemas lineares podem ser classificados conforme o número de soluções possíveis. Lembrando que a solução das equações é encontrada pela substituição das variáveis por valores.

Sistema Possível e Determinado (SPD): há apenas uma solução possível, o que acontece quando o determinante é diferente de zero (D ≠ 0).
Sistema Possível e Indeterminado (SPI): as soluções possíveis são infinitas.
Sistema Impossível (SI): não é possível apresentar qualquer tipo de solução.

As matrizes associadas a um sistema linear podem ser completas ou incompletas. São completas as matrizes que consideram os termos independentes das equações.

Os sistemas lineares são classificados como normais quando o número de equações é o mesmo que o número de incógnitas. Além disso, quando o determinante da matriz incompleta desse sistema não é igual a zero.

Solução de sistemas lineares por Regra de Cramer

A regra de Cramer é um método para classificar e solucionar sistemas lineares. Ele consiste no seguinte passo a passo:

1. Escrever a equação matricial do sistema.

Exemplo
A equação matricial do sistema $abre chaves atributos de tabela alinhamento de coluna left fim dos atributos linha com célula com reto x mais reto y igual a 2 fim da célula linha com célula com reto x menos reto y igual a 10 fim da célula fim da tabela fecha$ , é:

$abre colchetes tabela linha com 1 1 linha com 1 célula com menos 1 fim da célula fim da tabela fecha colchetes espaço. espaço abre colchetes tabela linha com reto x linha com reto y fim da tabela fecha colchetes igual a abre colchetes tabela linha com 2 linha com 10 fim da tabela fecha colchetes$

A primeira matriz é a dos coeficientes.

2. Calcular o determinante D, da matriz dos coeficientes:

$reto D igual a 1 espaço. espaço menos 1 espaço menos espaço parêntese esquerdo 1 espaço. espaço 1 parêntese direito espaço igual a espaço menos 1 espaço menos 1 espaço igual a espaço menos 2$

3. Calcular os determinantes Dx e Dy.

Para calcular Dx, substituímos na matriz dos coeficientes a primeira coluna pela matriz dos termos independentes.

$D x igual a abre colchetes tabela linha com 2 1 linha com 10 célula com menos 1 fim da célula fim da tabela fecha colchetes espaço igual a espaço 2 espaço. espaço parêntese esquerdo menos 1 parêntese direito espaço menos espaço parêntese esquerdo 1 espaço. espaço 10 parêntese direito espaço igual a espaço menos 2 espaço menos espaço 10 espaço igual a espaço menos 12$

Para calcular Dy, substituímos na matriz dos coeficientes a segunda coluna pela matriz dos termos independentes.

$D y igual a abre colchetes tabela linha com 1 2 linha com 1 10 fim da tabela fecha colchetes igual a 1 espaço. espaço 10 espaço menos espaço 2 espaço. espaço 1 espaço igual a espaço 10 menos 2 espaço igual a espaço 8$

4. Para determinar os valores de x e de y, calculamos uma razão entre o determinante de x ou y, pelo determinante principal D.

$reto x igual a Dx sobre reto D igual a numerador menos 12 sobre denominador menos 2 fim da fração igual a 6 reto y igual a Dy sobre reto D igual a numerador 8 sobre denominador menos 2 fim da fração igual a menos 4$

O par ordenado (6, -4) é a solução do sistema.

Classificação de sistemas lineares por Regra de Cramer

Para classificar um sistema de equações lineares utilizando o método de Cramer, analisamos os determinantes calculados.

Sistema possível e determinado (SPD): quando os determinantes são diferentes de zero.

$reto D não igual 0 Dx não igual 0 Dy não igual 0 ... Dn não igual 0$

Sistema possível e indeterminado (SPI): quando os determinantes são todos iguais a zero.

$reto D igual a 0 Dx igual a 0 Dy igual a 0 ... Dn igual a 0$

Sistema Impossível (SI): quando o determinante principal é igual a zero e os secundários diferentes de zero.

Veja que a divisão: $reto x igual a Dx sobre reto D igual a Dx sobre 0$ é impossível, pois não há divisão por zero.

Exercícios de sistemas lineares resolvidos

Vamos resolver passo a passo cada equação a fim de classificá-las em SPD, SPI ou SI.

Exercício 1
Classifique o sistema linear com 2 equações.

Exercício 2
Classifique o sistema linear com 3 equações.

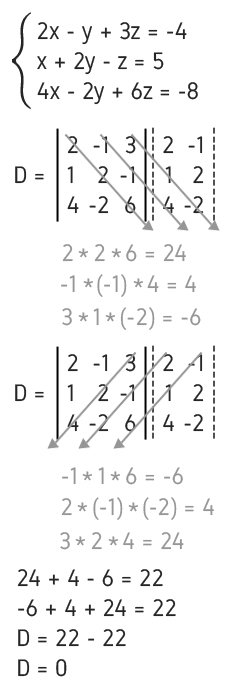
Se D = 0, podemos estar diante de um SPI ou de um SI.

Aprenda mais sobre:

Pratique com Exercícios de sistemas lineares resolvidos.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.