Teorema de Laplace: aplicação e exemplo

Rafael C. Asth

Professor de Matemática e Física

O Teorema de Laplace é um método para calcular o determinante de matrizes quadradas de ordemn, ou seja, de qualquer ordem.

Esse método é frequentemente utilizado em matrizes de ordem igual ou superior a 4, dado que, para matrizes de ordens menores, há outros métodos, por vezes mais rápidos.

Esse método foi desenvolvido pelo matemático e físico Pierre-Simon Laplace (1749 –1827).

Passos do Teorema de Laplace

Para calcular os determinantes, devemos seguir os seguintes passos:

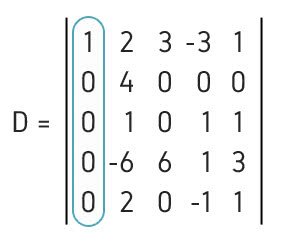
1. Selecionar uma fila qualquer (linha ou coluna), dando preferência a fila que contenha a maior quantidade de elementos iguais a zero, por tornar os cálculos mais simples;
2. Somar os produtos dos números da fila selecionada pelos seus respectivos cofatores.

Cálculo do cofator

O cofator de uma matriz de ordem n ≥ 2 é definido como:

Onde

A_ij: cofator de um elemento a_ij
i: linha onde se encontra o elemento
j: coluna onde se encontra o elemento
D_ij: é o determinante da matriz resultante da eliminação da linha i e da coluna j.

Exemplo de cálculo do cofator

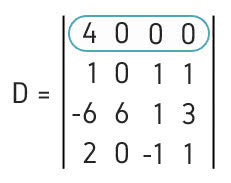
Determine o cofator do elemento a_23, da matriz A indicada.

Resolução

Para calcular o cofator do elemento a₂₃, comecemos calculando o determinante da matriz resultante da eliminação da linha 2 e da coluna 3.

Assim, calcularemos o determinante dessa matriz:

O cofator será encontrado substituindo o valor de D₂₃ na expressão, conforme indicado abaixo:

A_{23 =} (-1)²⁺³ . 1 = -1

O cofator A₂₃, do elemento a₂₃ da matriz dada, é igual a -1.

Agora que já sabemos determinar o cofator de um elemento de uma matriz, podemos então aplicar o teorema de Laplace para calcular o seu determinante.

Cálculo de determinante com o Teorema de Laplace

Encontre o determinante da matriz B, indicada abaixo.

Resolução

Selecionamos a linha 1, visto possuir um elemento igual a zero.

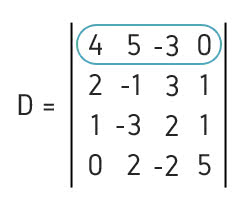
O determinante será encontrado fazendo:

Onde,

• é o determinante da matriz B;
• são os elementos da linha 1 (4, 5, -3, 0);
• são os correspondentes cofatores de cada elemento da linha 1.

A partir daqui, como zero multiplicado por qualquer número é zero, o cálculo fica mais simples, pois neste caso a₁₄ . A₁₄ não precisa ser calculado.

Vamos então calcular cada cofator:

Note que para determinar o cofator é necessário calcular o determinante de cada matriz de ordem 3 indicada acima. Para esse tipo de matriz, é mais prático aplicar a regra de Sarrus.

Relembre a Regra de Sarrus.

Substituindo os valores encontrados na expressão do determinante, temos:

Chegamos ao resultado 210, sendo o determinante da matriz ou, matriz de 4.ª ordem.

Exercício sobre Teorema de Laplace

Utilizando o Teorema de Laplace, calcule o determinante da matriz 5x5 indicada abaixo.

Para saber mais, veja também:

• Matrizes e Determinantes
• Matrizes
• Matrizes - Exercícios
• Matriz Inversa
• Sistemas Lineares
• Regra de Cramer

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.