Matriz Inversa

Rosimar Gouveia

Professora de Matemática e Física

A matriz inversa ou matriz invertível é um tipo de matriz quadrada, ou seja, que possui o mesmo número de linhas (m) e colunas (n).

Ela ocorre quando o produto de duas matrizes resulta numa matriz identidade de mesma ordem (mesmo número de linhas e colunas).

Assim, para encontrar a inversa de uma matriz, utiliza-se a multiplicação.

A . B = B . A = I_n (quando a matriz B é inversa da matriz A)

Mas o que é Matriz Identidade?

A Matriz Identidade é definida quando os elementos da diagonal principal são todos iguais a 1 e os outros elementos são iguais a 0 (zero). Ela é indicada por I_n:

Propriedades da Matriz Inversa

• Existe somente uma inversa para cada matriz
• Nem todas as matrizes possuem uma matriz inversa. Ela é invertível somente quando os produtos de matrizes quadradas resultam numa matriz identidade (I_n)
• A matriz inversa de uma inversa corresponde à própria matriz: A = (A^-1)^-1
• A matriz transposta de uma matriz inversa também é inversa: (A^t) ^-1 = (A^-1)^t
• A matriz inversa de uma matriz transposta corresponde à transposta da inversa: (A^-1 A^t)-1
• A matriz inversa de uma matriz identidade é igual à matriz identidade: I^-1 = I

Veja também: Matrizes

Exemplos de Matriz Inversa

Matriz Inversa 2x2

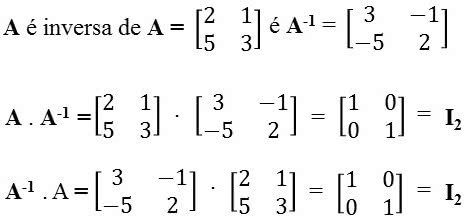
Matriz Inversa 3x3

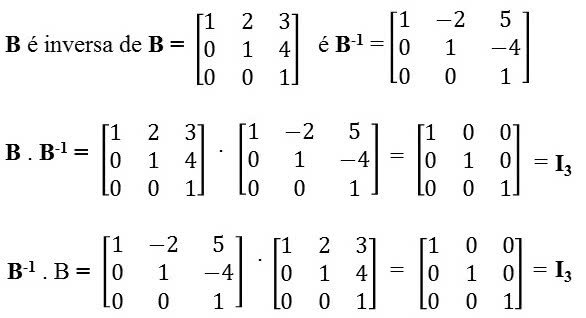
Passo a Passo: Como Calcular a Matriz Inversa?

Sabemos que se o produto de duas matrizes é igual a matriz identidade, essa matriz possui uma inversa.

Observe que se a matriz A for inversa da matriz B, utiliza-se a notação: A^-1.

Exemplo: Encontre a inversa da matriz abaixo de ordem 3x3.

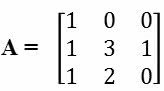
Antes de mais nada, devemos lembrar que A . A^-1 = I (A matriz multiplicada por sua inversa resultará na matriz identidade I_n).

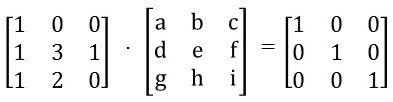
Multiplica-se cada elemento da primeira linha da primeira matriz por cada coluna da segunda matriz.

Por conseguinte, multiplicam-se os elementos da segunda linha da primeira matriz pelas colunas da segunda.

E por fim, a terceira linha da primeira com as colunas da segunda:

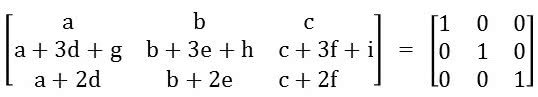
Fazendo a equivalência dos elementos com a matriz identidade, podemos descobrir os valores de:

a = 1
b = 0
c = 0

Sabendo esses valores, podemos calcular as outras incógnitas da matriz. Na terceira linha e primeira coluna da primeira matriz temos que a + 2d = 0. Portanto, vamos começar por encontrar o valor de d, pela substituição dos valores encontrados:

1 + 2d = 0
2d = -1
d = -1/2

Da mesma maneira, na terceira linha e segunda coluna podemos encontrar o valor de e:

b + 2e = 0
0 + 2e = 0
2e = 0
e = 0/2
e = 0

Continuando, temos na terceira linha da terceira coluna: c + 2f. Note que segunda a matriz identidade dessa equação não é igual a zero, mas igual a 1.

c + 2f = 1
0 + 2f = 1
2f = 1
f = ½

Passando para a segunda linha e a primeira coluna vamos encontrar o valor de g:

a + 3d + g = 0
1 + 3. (-1/2) + g = 0
1 – 3/2 + g = 0
g = -1 + 3/2
g = ½

Na segunda linha e segunda coluna, podemos encontrar o valor de h:

b + 3e + h = 1
0 + 3 . 0 + h = 1
h = 1

Por fim, vamos encontrar o valor de i pela equação da segunda linha e terceira coluna:

c + 3f + i = 0
0 + 3 (1/2) + i = 0
3/2 + i = 0
i = 3/2

Depois de descobertos todos os valores das incógnitas, podemos encontrar todos os elementos que compõem a matriz inversa de A:

Exercícios de Vestibular com Gabarito

1. (Cefet-MG) A matriz 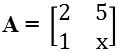é inversa de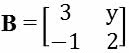
Pode-se afirmar, corretamente, que a diferença (x-y) é igual a:

a) -8
b) -2
c) 2
d) 6
e) 8

2. (U.F. Viçosa-MG) Sejam as matrizes:

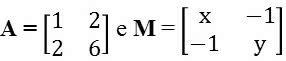
Onde x e y são números reais e M é a matriz inversa de A. Então o produto xy é:

a) 3/2
b) 2/3
c) 1/2
d) 3/4
e) 1/4

3. (PUC-MG) A matriz inversa da matriz 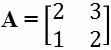é igual a:

a)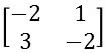
b)
c)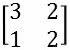
d)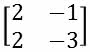
e)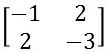

Leia também:

• Matrizes - Exercícios
• Tipos de Matrizes
• Matriz Identidade
• Matriz Transposta
• Multiplicação de Matrizes
• Regra de Cramer
• Teorema de Laplace

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.