Regra de Sarrus: passo a passo e exemplos

Rafael C. Asth

Professor de Matemática e Física

Regra de Sarrus é um método prático usado para encontrar o determinante de uma matriz quadrada de ordem 3, sendo o determinante um número associado a uma matriz quadrada. Seu cálculo depende da ordem da matriz.

Para encontrar o determinante de uma matriz quadrada genérica do tipo 3 x 3 (3 linhas e 3 colunas), fazemos as seguintes operações:

$d e t espaço A igual a abre barra vertical tabela linha com célula com a com 11 subscrito fim da célula célula com a com 12 subscrito fim da célula célula com a com 13 subscrito fim da célula linha com célula com a com 21 subscrito fim da célula célula com a com 22 subscrito fim da célula célula com a com 23 subscrito fim da célula linha com célula com a com 31 subscrito fim da célula célula com a com 32 subscrito fim da célula célula com a com 33 subscrito fim da célula fim da tabela fecha barra vertical espaço seta dupla para a direita$

$det espaço reto A igual a reto a com 11 subscrito. reto a com 22 subscrito. reto a com 33 subscrito mais reto a com 12 subscrito. reto a com 23 subscrito. reto a com 31 subscrito mais reto a com 13 subscrito. reto a com 21 subscrito. reto a com 32 subscrito menos reto a com 13 subscrito. reto a com 22 subscrito. reto a com 31 subscrito menos reto a com 11 subscrito. reto a com 23 subscrito. reto a com 32 subscrito menos reto a com 12 subscrito. reto a com 21 subscrito. reto a com 33 subscrito$

Há diversos elementos da matriz A se multiplicando e, a cada resultado, realizam-se adições e subtrações.

Como não é prático memorizar esta sequência, chegamos até ela por uma sequência de passos conhecida como Regra de Sarrus.

Regra de Sarrus: passo a passo

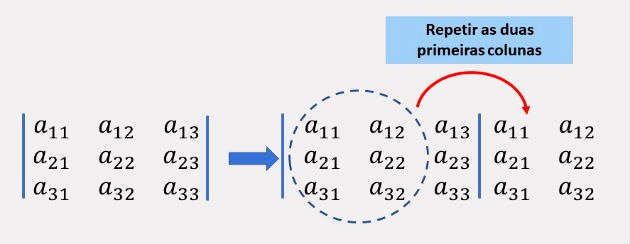
Aplicam-se os seguintes passos, exatamente nesta ordem:

1º passo

Repetir ao lado direito da matriz suas duas primeiras colunas.

2º passo

Multiplicar os elementos nas diagonais principais, com o sinal de mais na frente de cada termo.

Observe serem tomadas as diagonais que apresentam 3 elementos.

O resultado será:

$começar estilo tamanho matemático 18px reto a com 11 subscrito. reto a com 22 subscrito. reto a com 33 subscrito espaço mais espaço reto a com 12 subscrito. reto a com 23 subscrito. reto a com 31 subscrito espaço mais espaço reto a com 13 subscrito. reto a com 21 subscrito. reto a com 32 subscrito fim do estilo$

3º passo

Multiplicam-se os elementos nas diagonais secundárias, trocando o sinal do produto encontrado.

O resultado será:

$começar estilo tamanho matemático 18px menos espaço reto a com 13 subscrito. reto a com 22 subscrito. reto a com 31 subscrito espaço menos espaço reto a com 11 subscrito. reto a com 23 subscrito. reto a com 32 subscrito espaço menos espaço reto a com 12 subscrito. reto a com 21 subscrito. reto a com 33 subscrito fim do estilo$

4º passo

Juntar os termos resolvendo as adições e subtrações. O resultado será igual ao determinante.

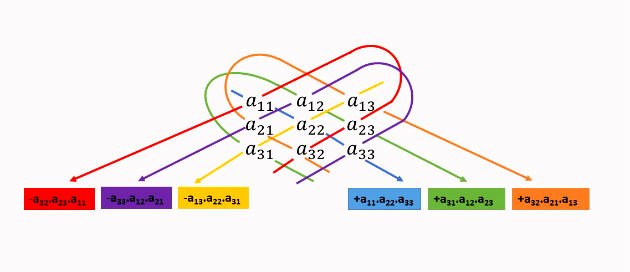
Outra representação para a Regra de Sarrus

A regra de Sarrus pode ainda ser feita considerando o seguinte esquema:

Leia também: Matrizes e Tipos de Matrizes

Exemplo 1

Considere a matriz abaixo e calcule seu determinante.

$M igual a abre colchetes tabela linha com 1 3 5 linha com 2 4 1 linha com célula com menos 4 fim da célula 1 célula com menos 1 fim da célula fim da tabela fecha colchetes$

Resolução

Para encontrar o determinante da matriz indicada, aplicaremos a regra de Sarrus. Para isso, repetimos as duas primeiras colunas e multiplicamos as diagonais, conforme esquema abaixo:

$det espaço reto M igual a mais 80 menos 1 mais 6 menos 4 menos 12 mais 10 igual a 79 det espaço reto M igual a 79$

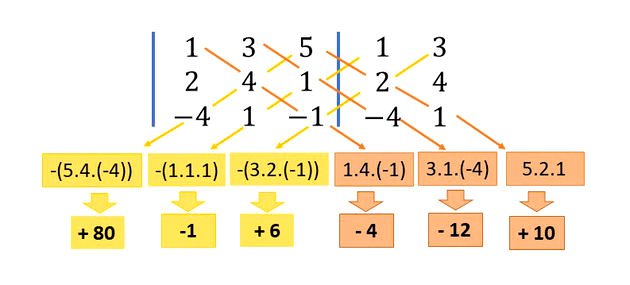
O determinante da matriz M é igual a 79.

Exemplo 2

Calcule o determinante da matriz.

$A igual a abre colchetes tabela linha com 3 2 1 linha com célula com menos 1 fim da célula célula com menos 2 fim da célula 0 linha com 0 2 1 fim da tabela fecha colchetes$ .

Resolução

Sendo uma matriz de ordem 3, usaremos a regra de Sarrus, conforme o esquema abaixo:

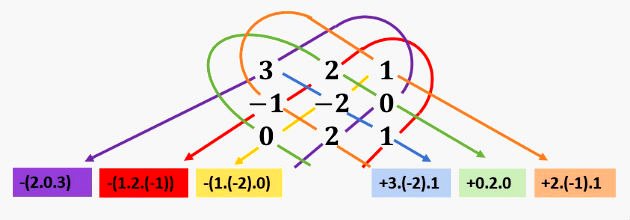
Resolvendo as multiplicações, temos:

$det espaço reto A igual a 3. parêntese esquerdo menos espaço 2 parêntese direito.1 mais 0.2.0 mais 2. parêntese esquerdo menos espaço 1 parêntese direito.1 menos parêntese esquerdo 1. parêntese esquerdo menos espaço 2 parêntese direito.0 parêntese direito menos parêntese esquerdo 2.0.3 parêntese direito menos parêntese esquerdo 1.2. parêntese esquerdo menos 1 parêntese direito parêntese direito igual a menos 6 menos 2 mais 2 det espaço reto A igual a menos 6 mais 0 menos 2 mais 2 mais 0 mais 2 det espaço reto A igual a menos 6 mais 2 det espaço reto A igual a menos 4$

Assim, o determinante da matriz A é igual a - 4.

Para saber mais sobre esse assunto, veja também:

Exercícios sobre a Regra de Sarrus

Exercício 1

Qual o valor do x para que o determinante da matriz abaixo seja igual a zero?

$A igual a abre colchetes tabela linha com 2 1 2 linha com 3 2 4 linha com 1 x célula com parêntese esquerdo x mais 2 parêntese direito fim da célula fim da tabela fecha colchetes$

Ver Resposta

Para resolver essa questão, vamos aplicar a regra de Sarrus igualando o determinante a zero, conforme esquema abaixo:

det A = 2.2.(x + 2) + 1.4.1 + 2.3.x - (2.2.1) - (2.4.x) - (1.3.(x+2)) = 0
4x +8 + 4 + 6x - 4 - 8x - 3x -6 = 0
4x + 6x - 8x - 3x = 4 + 6 -8 -4
10x - 11x = 10 - 12
- 1 x = -2
x = 2

Exercício 2

Seja A = (a_ij) a matriz quadrada de ordem 3, onde

$reto a com ij subscrito igual a abre chaves tabela linha com célula com reto i mais 2 vírgula espaço se espaço reto i menor que reto j fim da célula linha com célula com reto i mais reto j vírgula espaço se espaço reto i igual a reto j fim da célula linha com célula com reto j menos 1 vírgula espaço se espaço reto i maior que reto j fim da célula fim da tabela fecha$ .

O valor do determinante de A é igual a:

a) -40
b) 56
c) 40
d) -56
e) 0

Confira a resolução do exercício no vídeo abaixo.

regradesarrusvideo Ver no YouTube

Ver Resposta

Alternativa: c) 40

Veja mais em Matrizes - Exercícios.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.