Números Racionais

Rafael C. Asth

Professor de Matemática e Física

Os números racionais são os números que podem ser escritos na forma de fração. Esses números podem também ter representação decimal finita ou decimal infinita e periódica.

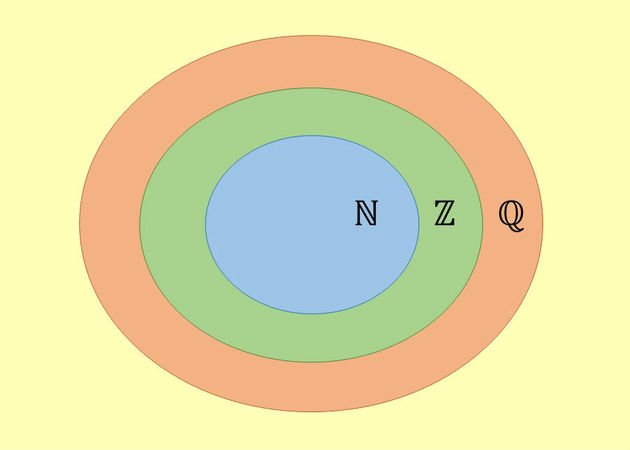
Observe que o conjunto dos números racionais, representado por $reto números racionais$ , contém o conjunto dos números inteiros, que por sua vez contém o conjunto dos números naturais, ou seja, $reto números naturais subconjunto reto números inteiros subconjunto reto números racionais$ .

O conjunto dos números racionais pode ser representado por:

$reto números racionais igual a abre chaves a sobre b linha vertical a pertence reto números inteiros espaço e espaço b pertence reto números inteiros asterisco fecha chaves$

A definição do conjunto $reto números racionais$ pode ser lida como: um quociente entre um número a por um número b, tal que, a pertença ao conjunto dos números inteiros, e b pertença ao conjunto dos números inteiros sem o zero.

Todo número natural $reto números naturais$ é um número inteiro, assim como todo número inteiro $reto números inteiros$ , é um número racional $reto números racionais.$

Exemplos de Números Racionais

Números Inteiros

Todo número inteiro pode ser escrito como uma divisão de outros dois números inteiros.

$começar estilo tamanho matemático 18px negrito 2 negrito igual a negrito 2 sobre negrito 1 negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito 5 negrito igual a negrito 5 sobre negrito 1 negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito menos negrito 7 negrito igual a negrito menos negrito 7 sobre negrito 1 fim do estilo$

Números decimais finitos

Todo número decimal com um número finito de casas depois da vírgula, pode ser escrito como uma divisão entre dois números inteiros.

$começar estilo tamanho matemático 18px negrito 0 negrito vírgula negrito 2 negrito igual a negrito 2 sobre negrito 10 negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito 0 negrito vírgula negrito 06 negrito igual a negrito 6 sobre negrito 100 negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito 2 negrito vírgula negrito 173 negrito igual a negrito 2173 sobre negrito 1000 fim do estilo$

Números Periódicos (Dízimas periódicas)

Todo número decimal com um número infinito de casas depois da vírgula, que se repetem periodicamente, pode ser escrito como uma divisão entre dois números inteiros.

$começar estilo tamanho matemático 18px negrito 0 negrito vírgula negrito 333 negrito. negrito. negrito. negrito igual a negrito 3 sobre negrito 9 negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito 0 negrito vírgula negrito 24141 negrito. negrito. negrito. negrito igual a negrito 239 sobre negrito 990 negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito 2 negrito vírgula negrito 77 negrito. negrito. negrito. negrito igual a negrito 25 sobre negrito 9 negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço negrito espaço fim do estilo$

Subconjuntos do conjunto $reto números racionais$

Racionais não-nulos. Esse subconjunto é formado pelos números racionais sem o zero (0)
$reto números racionais asterisco igual a abre chaves x pertence reto números racionais linha vertical x não igual 0 fecha chaves$
Um número x que pertença aos Racionais, tal que x seja diferente de zero.

Racionais não-negativos. Subconjunto composto pelos números racionais positivos e o zero.
$reto números racionais com mais subscrito igual a abre chaves x pertence reto números racionais linha vertical x maior ou igual a 0 fecha chaves$
Um número x que pertença aos Racionais, tal que x seja maior ou igual a zero.

Racionais não-positivos. Números racionais negativos e o zero formam esse subconjunto.
$reto números racionais com menos subscrito igual a abre chaves x pertence reto números racionais linha vertical x menor ou igual a 0 fecha chaves$
Um número x que pertença aos Racionais, tal que x seja menor ou igual a zero.
Racionais positivos. Esse subconjunto é composto pelos números racionais positivos. $reto números racionais à potência de asterisco com mais subscrito igual a abre chaves x pertence reto números racionais linha vertical x maior que 0 fecha chaves$
Um número x que pertença aos Racionais, tal que x seja maior que zero.
Racionais negativos. Subconjunto formado pelos números racionais negativos. $reto números racionais à potência de asterisco com menos subscrito igual a abre chaves x pertence reto números racionais linha vertical x menor que 0 fecha chaves$
Um número x que pertença aos Racionais, tal que x seja menor que zero.

Exercícios Resolvidos

Questão 1

Assinale Verdadeiro (V) ou Falso (F):

a) 0,212121... é um número racional
b) 5/3 não é um número racional
c) -1 é um número racional
d) O oposto de 13/5 é -13/5
e) 1,41421356... é um número racional

Ver Resposta

a) V
b) F
c) V
d) V
e) F

Questão 2

Represente as frações em números decimais:

a) 375/200
b) 30/11
c) 3/5
d) 4/3
e) -7/50

Ver Resposta

a) 1,875
b) 2,727272...
c) 0,6
d) 1,333...
e) -0,14

Pratique mais com Exercícios sobre Números Racionais.

Curiosidade

A letra que representa o conjunto dos números racionais, ou seja, o "Q" é derivado da palavra inglesa "quotient", que significa quociente.

Leia também:

Rafael C. Asth

Professor de Matemática, licenciado e pós-graduado em ensino da Matemática e da Física. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.