Teoria dos conjuntos: entenda o que é (com exemplos)
A teoria dos conjuntos é um ramo da matemática que estuda a coleção de objetos, chamados de elementos.
Dessa forma, os elementos (que podem ser qualquer coisa: números, pessoas, frutas) são indicados por letra minúscula e definidos como um dos componentes do conjunto.
Exemplo: o elemento “a” ou a pessoa “x”.
Enquanto os elementos do conjunto são indicados por letra minúscula, os conjuntos, são representados por letras maiúsculas e, normalmente, com chaves { }.
Além disso, os elementos são separados por vírgula ou ponto e vírgula, por exemplo:
A = {a, e, i, o, u}
Representação dos conjuntos
Um conjunto pode ser representado de algumas maneiras. Cada uma delas têm vantagens e desvantagens, a depender do problema ou da situação em sejam usados.
Diagrama de Euler-Venn
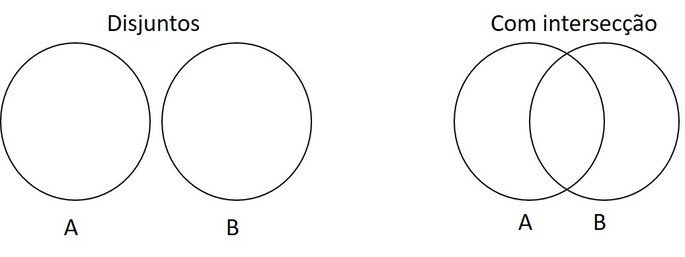
No modelo de Diagrama de Euler-Venn (Diagrama de Venn), os conjuntos são representados graficamente. Imagens como círculos, elipses e retângulos formam uma área que “guarda” seus elementos.
Esta figura plana fechada é chamada de diagrama.
Os diagramas de Venn são úteis para representar conjuntos disjuntos (nenhum elemento em comum), assim como, conjuntos com elementos que se repetem.
Representação de conjuntos na forma tabular
A forma tabular utiliza os símbolos de chaves { } para representar conjuntos. Seus elementos devem estar separados por vírgulas.
Exemplos
A = {1, 3, 9, 12, 17}
B = {João, Luíza, Fernando, Lívia}
Representação de conjuntos por uma propriedade
Um conjunto pode ser representado por uma regra que define uma característica comum em seus elementos.
Exemplos
A = {x / x é uma vogal} lemos: “O conjunto A é formado pelos elementos x, tal que x é uma vogal”.
B = {x / x é múltiplo de 3} lemos: “O conjunto B é formado pelos elementos x, tal que x pertença aos números naturais e seja um múltiplo de 3.”
Relação de Pertinência
A relação de pertinência é um conceito muito importante na "Teoria dos Conjuntos".
Ela indica se o elemento pertence () ou não pertence (
) ao determinado conjunto, por exemplo:
D = {w,x,y,z}
Logo,
(w pertence ao conjunto D)
(j não pertence ao conjunto D)
Isso significa que a pertinência é uma relação entre elementos e conjuntos.
Relação de Inclusão
A relação de inclusão aponta se tal conjunto está contido (C), não está contido (Ȼ) ou se um conjunto contém (Ɔ), algum subconjunto.
Exemplo:
A = {a,e,i,o,u}
B = {a,e,i,o,u,m,n,o}
C = {p,q,r,s,t}
Logo,
A C B (A está contido em B, ou seja, todos os elementos de A estão em B).
C Ȼ B (C não está contido em B, pois os elementos dos conjuntos são diferentes).
B Ɔ A (B contém A, pois todos elementos de A estão em B).
Conjunto Vazio
O conjunto vazio é o conjunto em que não há elementos; é representado por duas chaves { } ou pelo símbolo Ø. Note que o conjunto vazio está contido (C) em todos os conjuntos.
União, Intersecção e diferença entre conjuntos
As operações entre conjuntos são fundamentais para a solução de problemas. Cada operação possui suas características e regras.
União de conjuntos
A união, representada pela letra (U), corresponde a junção dos elementos de dois ou mais conjuntos, sem repetir elementos comuns.
Exemplo
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
Logo,
A U B = {1, 2, 3, 4, 5, 6}
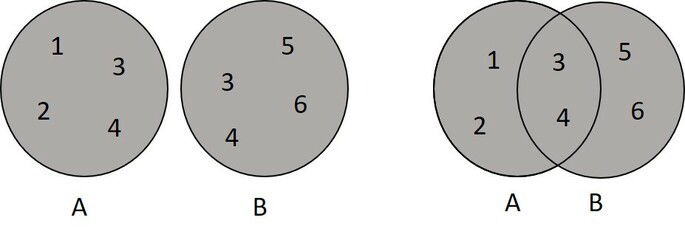
Repare que os algarismos 3 e 4 foram representados uma única vez, mesmo estando presentes em A e B.
Ao utilizar diagramas de Venn, a união é representada pelo preenchimento de toda imagem, não importando se são ou não disjuntos.
Intersecção de conjuntos
A intersecção, representada pelo símbolo (∩), corresponde aos elementos em comum de dois ou mais conjuntos.
Assim, a intersecção é um novo conjunto, formado apenas pelos elementos que se repetem nos conjuntos iniciais.
Exemplo
C = {a, b, c, d, e}
D = {d, e, f, g, h}
Logo,
C ∩ D = {d, e}
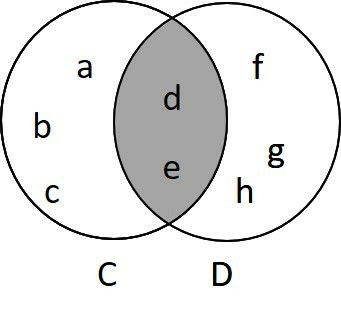
Ao utilizar diagramas de Venn, a intersecção é representada pintando apenas a área onde os conjuntos estejam sobrepostos.
Essa área “guarda” apenas os elementos repetidos.
Diferença de conjuntos
A diferença corresponde ao conjunto de elementos que estão no primeiro conjunto, e não aparecem no segundo,
Exemplo
A = {a, b, c, d, e} - B = {b, c, d, f, g}
Logo,
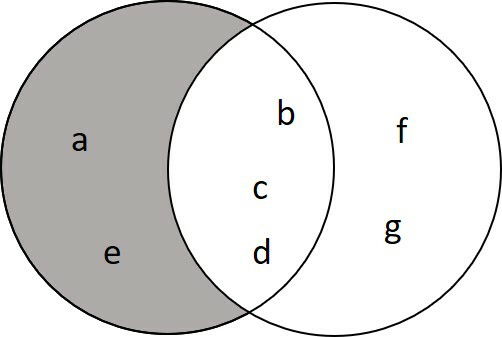
A - B = {a, e}
Veja que a operação retirou os elementos comuns que existem em B.
Na forma de diagrama, representamos como:
Atenção!
A subtração não é comutativa, ou seja, B - A não é igual à A - B.
B - A = {f, g}
Igualdade dos Conjuntos
Na igualdade dos conjuntos, os elementos de dois conjuntos são idênticos, por exemplo, nos conjuntos A e B:
A = {1,2,3,4,5}
B = {3,5,4,1,2}
Logo,
A = B (A igual a B).
Conjuntos Numéricos
Os conjuntos numéricos são formados pelos:
- Números Naturais: N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12...}
- Números Inteiros: Z = {..., -3, -2, -1, 0, 1, 2, 3...}
- Números Racionais: Q = {..., -3, -2, -1, 0, 1, 2, 3,4,5,6...}
- Números Irracionais: I = {..., √2, √3, √7, 3, 141592…}
- Números Reais: R = N (números naturais) + Z (números inteiros) + Q (números racionais) + I (números irracionais)
Teste os seus conhecimentos com:
Ou aprofunde os seus estudos sobre o assunto com:
- Operações com Conjuntos
- Diagrama de Venn
- Símbolos Matemáticos
- Símbolos dos conjuntos
- Conjuntos numéricos
- Números: o que são, história e conjuntos
ASTH, Rafael. Teoria dos conjuntos: entenda o que é (com exemplos). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/teoria-dos-conjuntos/. Acesso em:


