Números Inteiros

Rafael C. Asth
Rafael C. Asth
Professor de Matemática e Física

Os números inteiros são os números positivos e negativos, que não apresentam parte decimal e, o zero. Estes números formam o conjunto dos números inteiros, indicado por ℤ.

Não pertencem aos números inteiros: as frações, números decimais, os números irracionais e os complexos.

O conjunto dos números inteiros é infinito e pode ser representado da seguinte maneira:

ℤ = {..., - 3, - 2, - 1, 0, 1, 2, 3,...}

Os números inteiros negativos são sempre acompanhados pelo sinal (-), enquanto os números inteiros positivos podem vir ou não acompanhados de sinal (+).

O zero é um número neutro, ou seja, não é um número nem positivo e nem negativo.

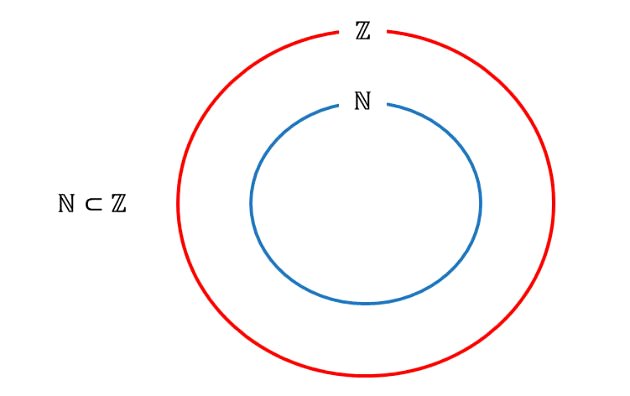
A relação de inclusão no conjunto dos inteiros envolve o conjunto dos números naturais (ℕ).

Todo número inteiro possui um antecessor e um sucessor. Por exemplo, o antecessor de -3 é -4, já o seu sucessor é o -2.

Representação na Reta Numérica

Os números inteiros podem ser representados por pontos na reta numérica. Nesta representação, a distância entre dois números consecutivos é sempre a mesma.

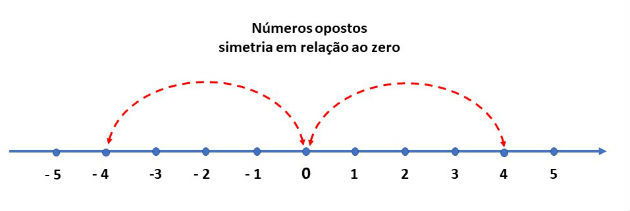
Os números que estão a uma mesma distância do zero, são chamados de opostos ou simétricos.

Por exemplo, o -4 é o simétrico de 4, pois estão a uma mesma distância do zero, conforme assinalado na figura abaixo:

Números opostos

Subconjuntos de ℤ

O conjunto dos números naturais (ℕ) é um subconjunto de ℤ, pois está contido no conjunto dos números inteiros. Assim:

Subconjunto dos naturais

Além do conjunto dos números naturais, destacamos os seguintes subconjuntos de ℤ:

  • ℤ* : é o subconjunto dos números inteiros, com exceção do zero. ℤ* = {..., -3,-2,-1, 1, 2, 3, 4, ...}
  • ℤ+ : são os números inteiros não-negativos, ou seja ℤ+ = {0, 1, 2, 3, 4, ...}
  • ℤ _ : é o subconjunto dos números inteiros não-positivos, ou seja ℤ_= {..., -4,-3,-2,-1, 0}
  • ℤ*+ : é o subconjunto dos números inteiros, com exceção dos negativos e do zero. ℤ*+ = {1,2,3,4, 5...}
  • ℤ*_ : são os números inteiros, com exceção dos positivos e do zero, ou seja ℤ*_= {..., -4,-3,-2,-1}

Leia também sobre Números: o que são, história e conjuntos.

Exercícios Resolvidos

Questão 1

Represente as seguintes situações com números positivos ou negativos.

a) Em Moscou, os termômetros marcaram cinco graus abaixo de zero nesta manhã.

b) No Rio de Janeiro hoje, os banhistas aproveitaram a praia sob uma temperatura de quarenta graus Celsius.

c) Marcos consultou seu saldo bancário e estava indicando dever R$150,00.

a) -5°C

b) 40°C

c) -R$150,00

Questão 2

Indique o antecessor e o sucessor dos seguintes números:

a) -34

b) -8

c) 0

a) -35 e -33

b) -9 e -7

c) -1 e 1

Questão 3

Determine o oposto (ou simétrico) dos seguintes números:

a) 9

b) -3

c) -145

d) 98

a )-9

b) 3

c) 145

d) -98

Questão 4

Construa uma reta numérica e destaque os números: 2, -3, -1, 4, -4.

______-4______-3______-2______ -1______0______1______ 2______3______4______

Questão 5

Faetec - RJ - 2015

Observe o segmento de reta abaixo, dividido em 5 segmentos congruentes:

Faetec 2015

Nele estão representados seis números reais. A quantidade de elementos do conjunto {A,B,C,D} que representa número inteiro é:

a) 0
b) 1
c) 2
d) 3
e) 4

Alternativa c: 2

Temos uma medida de 7,5 que vai de 2 a 9,5.

9,5 - 2 = 7,5

Como os segmentos são congruentes, tem a mesma medida, cada um tem 1,5.

7,5 / 5 = 1,5

Partindo de 2 e, somando 1,5, temos:

2 + 1,5 = 3,5. Portanto, A vale 3,5 e não é inteiro.

Continuando somando 1,5 ao anterior, obtemos:

B vale 5. É inteiro.

C vale 6,5. Não é inteiro.

D vale 8, É inteiro.

Dessa maneira, temos dois números inteiros.

Alternativa c: 2

Leia também:

Rafael C. Asth
Rafael C. Asth
Professor de Matemática, licenciado e pós-graduado em ensino da Matemática e da Física. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.
Veja também