Calor Latente

Rafael C. Asth

Professor de Matemática e Física

O calor latente, também chamado de calor de transformação, é uma grandeza física que designa a quantidade de calor recebida ou cedida por um corpo enquanto seu estado físico se modifica.

Importante destacar que durante a transformação a temperatura permanece a mesma, ou seja, constante.

Como exemplo, podemos pensar num cubo de gelo que está derretendo. Quando ele começa a mudar de estado físico (sólido para o líquido), a temperatura da água permanece a mesma nos dois estados.

Fórmula

Para calcular o calor latente é utilizada a fórmula:

$começar estilo tamanho matemático 18px reto Q espaço igual a espaço reto m espaço. espaço reto L fim do estilo$

Onde,

Q: quantidade de calor (cal ou J)
m: massa (g ou Kg)
L: calor latente (cal/g ou J/Kg)

No Sistema Internacional (SI), o calor latente é dado em J/Kg (Joule por quilograma). Mas também é usual ser medido em cal/g (caloria por grama).

Note que o calor latente pode apresentar valores negativos ou positivos. Sendo assim, se a substância estiver cedendo calor seu valor será negativo (processo exotérmico). Isso ocorre na solidificação e liquefação.

Por outro lado, se tiver recebendo calor, o valor será positivo (processo endotérmico). Isso ocorre na fusão e na vaporização.

Calor Latente de Vaporização

No calor latente ocorre a mudança de estado físico. Ou seja, a substância pode passar do estado sólido para o líquido, do líquido para o gasoso e vice-versa.

Quando a mudança é da fase líquida para a fase gasosa o calor latente é chamado calor de vaporização (Lv).

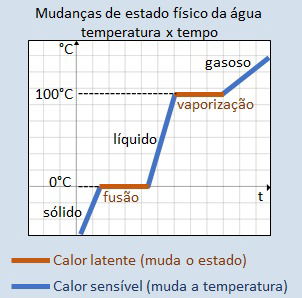
calor latente de vaporização da água é de 540 cal/g. Ou seja, são necessárias 540 cal para evaporar 1 g de água a 100 °C.

Nesse caso, a quantidade de calor necessária (Q) é proporcional à massa da substância (m):

$começar estilo tamanho matemático 18px reto Q espaço igual a espaço reto m espaço. espaço Lv fim do estilo$

onde,

Lv: é um valor constante que depende da substância.

Leia Estados Físicos da Água.

Calor Específico

O calor específico é a quantidade de calor necessária para aumentar a temperatura de 1 °C de 1g do elemento. Cada substância possui um calor específico, sendo uma propriedade do material.

Ele é calculado pela fórmula:

$reto c espaço igual a espaço numerador reto Q sobre denominador reto m espaço. espaço Δθ fim da fração espaço$ ou $reto c espaço igual a espaço reto C sobre reto m$

Onde,

c: calor específico (cal/g°C ou J/Kg.K)
Q: quantidade de calor (cal ou J)
m: massa (g ou Kg)
Δθ: variação de temperatura (°C ou K)
C: capacidade térmica (cal/°C ou J/K)

Calor Sensível

O calor sensível provoca mudanças de temperatura. É uma grandeza diferente do calor latente, pois modifica a temperatura sem alterar estado da substância.

Um exemplo é quando aquecemos uma barra de metal. O resultado será observado pelo aumento da temperatura do material, no entanto, seu estado sólido não se altera.

Para calcular o calor sensível utiliza-se a seguinte fórmula:

$começar estilo tamanho matemático 18px reto Q espaço igual a espaço reto m espaço. espaço reto c espaço. espaço Δθ fim do estilo$

Q: quantidade de calor sensível (cal ou J)
m: massa do corpo (g ou Kg)
c: calor específico da substância (cal/g°C ou J/Kg.°C)
Δθ: variação de temperatura (°C ou K)

Exercícios de Calor Latente

Exercício 1

(Unifor-CE) Um cubo de gelo de massa 100 g, inicialmente à temperatura de - 20 °C, é aquecido até se transformar em água a 40 °C (dados: calor específico do gelo 0,50 cal/g °C; calor específico da água 1,0 cal/g °C; calor de fusão do gelo 80 cal/g). As quantidades de calor sensível e de calor latente trocados nessa transformação, em calorias, foram, respectivamente:

a) 8.000 e 5.000
b) 5.000 e 8.000
c) 5.000 e 5.000
d) 4.000 e 8.000
e) 1.000 e 4.000

Ver Resposta

Resposta correta b) 5.000 e 8.000

O objetivo é determinar os calores latente e sensível. São as energias usadas para mudar de estado e alterar a temperatura.

Os dados são:

m=100 g
Fase inicial: gelo a -20°C
Fase final: água líquida a 40°C
calor específico do gelo 0,50 cal/g °C
calor específico da água 1,0 cal/g °C
calor de fusão do gelo 80 cal/g

Calculo do calor latente (fusão)

$Q espaço igual a espaço m. L Q espaço igual a espaço 100.80 espaço igual a espaço 8 espaço 000 espaço c a l$

Cálculo do calor sensível

O calor sensível acontece durante as fases sólida e líquida e queremos determinar o total durante o processo.

$Qtotal espaço igual a espaço Qgelo espaço mais espaço Qágua espaço líquida espaço Qtotal espaço igual a espaço reto m espaço. espaço reto c com gelo subscrito espaço. espaço incremento reto T espaço mais espaço reto m espaço. espaço reto c com líquido subscrito espaço. espaço incremento reto T Qtotal espaço igual a 100 espaço. espaço 0 vírgula 50 espaço. espaço parêntese esquerdo 0 espaço menos espaço parêntese esquerdo menos 20 parêntese direito parêntese direito espaço mais espaço 100 espaço. espaço 1 espaço. espaço parêntese esquerdo 40 espaço menos espaço 0 parêntese direito Qtotal espaço igual a 1 espaço 000 espaço mais espaço 4 espaço 000 Qtotal espaço igual a espaço 5 espaço 000$

Desta forma, os calores sensível e latente são, respectivamente, 5000 e 8000.

Exercício 2

(UNIP-SP) O calor específico latente de fusão do gelo é de 80 cal/g. Para fundir uma massa de gelo de 80g, sem variação de temperatura, a quantidade de calor latente necessária é de:

$a parêntese direito espaço 1 vírgula 0 espaço c a l$
$b parêntese direito espaço 6 vírgula 4 espaço c a l$
$c parêntese direito espaço 1 vírgula 0 espaço k c a l$
$d parêntese direito espaço 64 espaço k c a l$
$e parêntese direito espaço 6 vírgula 4.10 ao cubo espaço c a l$

Ver Resposta

Resposta correta: $e parêntese direito espaço 6 vírgula 4.10 ao cubo espaço c a l$

O calor latente é o produto entre a massa e o calor específico.

$Q espaço igual a espaço m espaço. espaço L Q espaço igual a espaço 80 espaço. espaço 80 espaço igual a espaço 6 espaço 400 espaço c a l$

Escrevendo em notação científica

$Q espaço igual a 6 vírgula 4 espaço. espaço 10 ao cubo espaço c a l$

Exercício 3

(FUVEST) Dispõe-se de água a 80°C e gelo a 0°C. Deseja-se obter 100gramas de água a uma temperatura de 40°C (após o equilíbrio), misturando água e gelo em um recipiente isolante e com capacidade térmica desprezível. Sabe-se que o calor específico latente de fusão do gelo é 80 cal/g e o calor específico sensível da água é 1,0 cal/g°C. A massa de gelo a ser utilizada é:

a) 5,0g
b) 12,5g
c) 25g
d) 33g
e) 50g

Ver Resposta

Alternativa c) 25g

Objetivo: determinar a massa de gelo que satisfaça as condições.

Dados:
Água líquida a 80°C;
Gelo a 0°C;
Calor específico latente de fusão do gelo é 80 cal/g (L);
Calor específico sensível da água é 1,0 cal/g°C (c);
massa total 100g

Equação 1:
$m com á g u a subscrito fim do subscrito mais m com g e l o subscrito fim do subscrito igual a 100 espaço g$

Modelo matemático a ser usado
No equilíbrio as transferências de calor serão iguais a zero.
$Q com g subscrito espaço mais espaço Q com a subscrito igual a 0$ (equação 2)

O gelo passa por dois processos: o de fusão a 0°C e o de aquecimento da fase líquida de 0°C à 40°C.
$Q com g subscrito igual a m com g subscrito. L espaço mais espaço m com g subscrito. c. incremento teta espaço$

A água líquida passa por uma redução de temperatura, neste processo, apenas o calor sensível age.
$Q com a subscrito igual a m com a subscrito. c. incremento teta$

Substituindo os calores da água e do gelo na equação 2, temos:
$m com g subscrito. L espaço mais espaço m com g subscrito. c. incremento teta espaço mais espaço m com a subscrito. c. incremento teta espaço igual a espaço 0$

Substituindo os valores fornecidos nos dados,

$m com g subscrito.80 espaço mais espaço m com g subscrito.1. parêntese esquerdo 40 espaço menos espaço 0 parêntese direito espaço mais espaço m com a subscrito.1. parêntese esquerdo 40 espaço menos espaço 80 parêntese direito espaço igual a espaço 0 80 espaço m com g subscrito espaço mais espaço 40 espaço m com g subscrito espaço menos 40 espaço m com a subscrito igual a 0 120 espaço m com g subscrito menos espaço 40 espaço m com a subscrito igual a 0 120 espaço m com g subscrito espaço igual a espaço 40 espaço m com a subscrito 120 sobre 40 m com g subscrito igual a espaço m com a subscrito 3 espaço m com g subscrito igual a espaço m com a subscrito$

Determinamos que a massa de gelo é três vezes a massa de água líquida.

Substituindo essa relação na equação 1:

$m com á g u a subscrito fim do subscrito mais m com g e l o subscrito fim do subscrito igual a 100 espaço g 3 espaço m com g e l o subscrito fim do subscrito espaço mais espaço m com g e l o subscrito fim do subscrito igual a 100 espaço g 4 espaço m com g e l o subscrito fim do subscrito igual a 100 g m com g e l o subscrito fim do subscrito igual a 100 sobre 4 igual a 25 espaço g$

Portanto, a massa de gelo deve ser de 25 g.

Pratique mais com exercícios de calor específico resolvidos e explicados

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações