Tabela Verdade

Rosimar Gouveia

Professora de Matemática e Física

Tabela verdade é um dispositivo utilizado no estudo da lógica matemática. Com o uso desta tabela é possível definir o valor lógico de uma proposição, isto é, saber quando uma sentença é verdadeira ou falsa.

Em lógica, as proposições representam pensamentos completos e indicam afirmações de fatos ou ideias.

Utiliza-se a tabela verdade em proposições compostas, ou seja, sentenças formadas por proposições simples, sendo que o resultado do valor lógico depende apenas do valor de cada proposição.

Para combinar proposições simples e formar proposições compostas são utilizados conectivos lógicos. Estes conectivos representam operações lógicas.

Na tabela abaixo, indicamos os principais conectivos, os símbolos usados para representá-los, a operação lógica que representam e o resultante valor lógico.

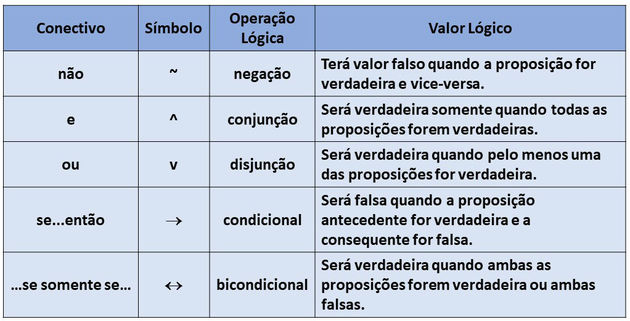
Exemplo

Indique o valor lógico (V ou F) de cada uma das proposição abaixo:

a) não p, sendo p: "π é um número racional".

Solução

A operação lógica que devemos fazer é a negação, desta forma, a proposição ~p pode ser definida como "π não é um número racional". Abaixo, apresentamos a tabela verdade desta operação:

Como "π é um número racional" é uma proposição falsa, então, de acordo com a tabela verdade acima, o valor lógico de ~p será verdadeiro.

b) π é um número racional e é um número irracional.

Solução

Neste caso, devemos encontrar o valor lógico da conjunção de duas proposições (p^q). A tabela verdade dessa operação lógica é:

Sendo a primeira proposição falsa e a segunda verdadeira, vemos, pela tabela verdade, que o valor lógico da proposição p^q será falso.

c) π é um número racional ou é um número irracional.

Solução

Considerando o conectivo de disjunção (p v q), podemos indicar a seguinte tabela verdade:

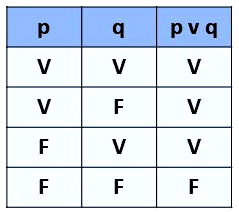
Como q é uma proposição verdadeira, então o valor lógico da proposição p v q também será verdadeiro conforme podemos verificar na tabela verdade acima.

d) Se π é um número racional, então é um número irracional.

Solução

Neste item, temos a operação lógica condicional p→q. A tabela verdade será igual a:

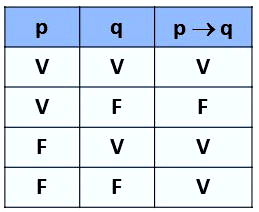
Sendo a primeira falsa e a segunda verdadeira, pela tabela concluímos que o resultado desta operação lógica será verdadeiro.

É importante notar que " é um número irracional" não é consequência do fato de "π é um número racional". O que o condicional representa é unicamente uma relação entre valores lógicos.

e) π é um número racional se somente se é um irracional.

Solução

Neste item, temos a operação lógica . A tabela verdade será igual a:

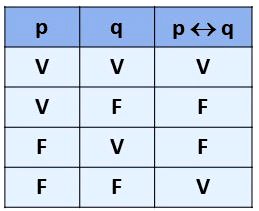
Pela tabela, concluímos que quando a primeira proposição é falsa e a segunda é verdadeira, o valor lógico será falso.

Construção de tabelas verdade

Na tabela verdade são colocados os valores lógicos possíveis (verdadeiro ou falso) para cada uma das proposições simples que formam a proposição composta e a combinação destes.

O número de linhas da tabela dependerá da quantidade de sentenças que compõem a proposição. A tabela verdade de uma proposição formada por n proposições simples terá 2ⁿ linhas.

Por exemplo, a tabela verdade da proposição "x é um número real e maior que 5 e menor que 10" terá 8 linhas, pois a sentença é formada por 3 proposições (n = 3).

Com o objetivo de colocarmos todas as possibilidades possíveis de valores lógicos na tabela, devemos preencher cada coluna com 2^n-k valores verdadeiros seguidos de 2^n-k valores falsos, com k variando de 1 até n.

Depois de preencher a tabela com os valores lógicos das proposições, devemos adicionar colunas relativas as proposições com os conectivos.

Exemplo

Construa a tabela verdade da proposição P(p,q,r) = p^q^r.

Solução

Neste exemplo, a proposição é formada por 3 sentenças (p, q e r). Para construir a tabela verdade, utilizaremos o seguinte esquema:

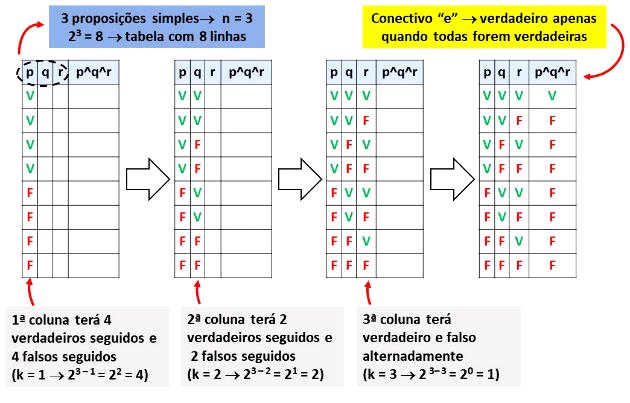
Portanto, a tabela verdade da sentença terá 8 linhas e será verdadeira quando todas as proposições também forem verdadeiras.

Confira nosso teste de raciocínio lógico.

Para saber mais, veja também:

• Raciocínio Lógico - Exercícios
• O que é lógica?
• Lógica Matemática
• Silogismo
• Lógica Aristotélica
• Método Dedutivo

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.