Exercícios de Raciocínio Lógico (questões com respostas)
Questões de raciocínio lógico são muito frequentes em diversos concursos, vestibulares e também na prova do Enem. Por isso, não perca a oportunidade de treinar esse tipo de questão com os exercícios resolvidos e comentados.
Questão 1
Descubra a lógica e complete o próximo elemento:
a) 1, 3, 5, 7, ___
b) 2, 4, 8, 16, 32, 64, ____
c) 0, 1, 4, 9, 16, 25, 36, ____
d) 4, 16, 36, 64, ____
e) 1, 1, 2, 3, 5, 8, ____
f) 2,10, 12, 16, 17, 18, 19, ____
Questão 2
(Enem) Jogar baralho é uma atividade que estimula o raciocínio. Um jogo tradicional é a Paciência, que utiliza 52 cartas. Inicialmente são formadas sete colunas com as cartas. A primeira coluna tem uma carta, a segunda tem duas cartas, a terceira tem três cartas, a quarta tem quatro cartas, e assim sucessivamente até a sétima coluna, a qual tem sete cartas, e o que sobra forma o monte, que são as cartas não utilizadas nas colunas.
A quantidade de cartas que forma o monte é
a) 21.
b) 24.
c) 26.
d) 28.
e) 31.
Questão 3
(UERJ) Em um sistema de codificação, AB representa os algarismos do dia do nascimento de uma pessoa e CD os algarismos de seu mês de nascimento. Nesse sistema, a data trinta de julho, por exemplo, corresponderia a:
Admita uma pessoa cuja data de nascimento obedeça à seguinte condição:
O mês de nascimento dessa pessoa é:
a) agosto
b) setembro
c) outubro
d) novembro
Questão 4
(FGV/TCE-SE) Duas tartarugas estavam juntas e começaram a caminhar em linha reta em direção a um lago distante. A primeira tartaruga percorreu 30 metros por dia e demorou 16 dias para chegar ao lago. A segunda tartaruga só conseguiu percorrer 20 metros por dia e, portanto, chegou ao lago alguns dias depois da primeira. Quando a primeira tartaruga chegou ao lago, o número de dias que ela teve que esperar para a segunda tartaruga chegar foi:
a) 8
b) 9
c) 10
d) 12
e) 15
Questão 5
(FGV/TRT-SC) Alguns consideram que a cidade de Florianópolis foi fundada no dia 23 de março de 1726, que caiu em um sábado. Após 90 dias, no dia 21 de junho, a data assinalou o início do inverno, quando a noite é a mais longa do ano. Esse dia caiu em uma:
a) segunda-feira
b) terça-feira
c) quarta-feira
d) quinta-feira
e) sexta-feira
Questão 6

Questão 7

Questão 8
(Enem) As figuras a seguir exibem um trecho de um quebra-cabeças que está sendo montado. Observe que as peças são quadradas e há 8 peças no tabuleiro da figura A e 8 peças no tabuleiro da figura B. As peças são retiradas do tabuleiro da figura B e colocadas no tabuleiro da figura A na posição correta, isto é, de modo a completar os desenhos.
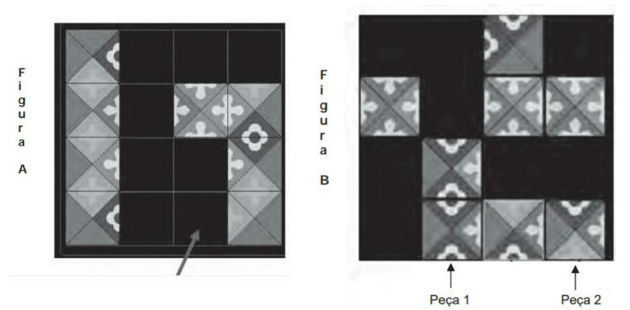
É possível preencher corretamente o espaço indicado pela seta no tabuleiro da figura A colocando a peça
a) 1 após girá-la 90° no sentido horário.
b) 1 após girá-la 180° no sentido anti-horário.
c) 2 após girá-la 90° no sentido anti-horário.
d) 2 após girá-la 180° no sentido horário.
e) 2 após girá-la 270° no sentido anti-horário.
Questão 9
(FGV/CODEBA) A figura mostra a planificação das faces de um cubo.
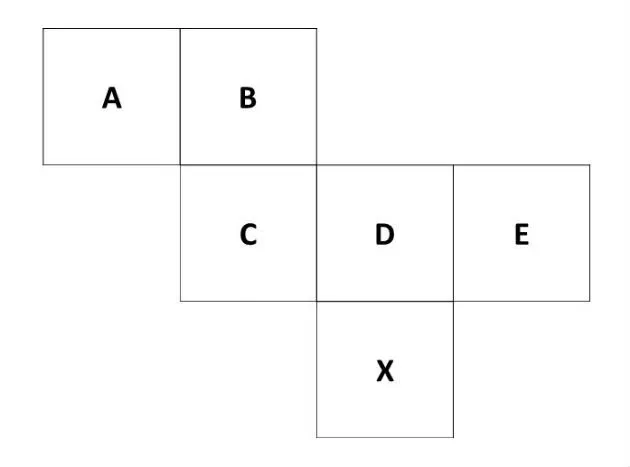
Nesse cubo, a face oposta à face X é
a) A
b) B
c) C
d) D
e) E
Questão 10
(Enem) João propôs um desafio a Bruno, seu colega de classe: ele iria descrever um deslocamento pela pirâmide a seguir e Bruno deveria desenhar a projeção desse deslocamento no plano da base da pirâmide.

O deslocamento descrito por João foi: mova-se pela pirâmide, sempre em linha reta, do ponto A ao ponto E, a seguir do ponto E ao ponto M, e depois de M a C. O desenho que Bruno deve fazer é
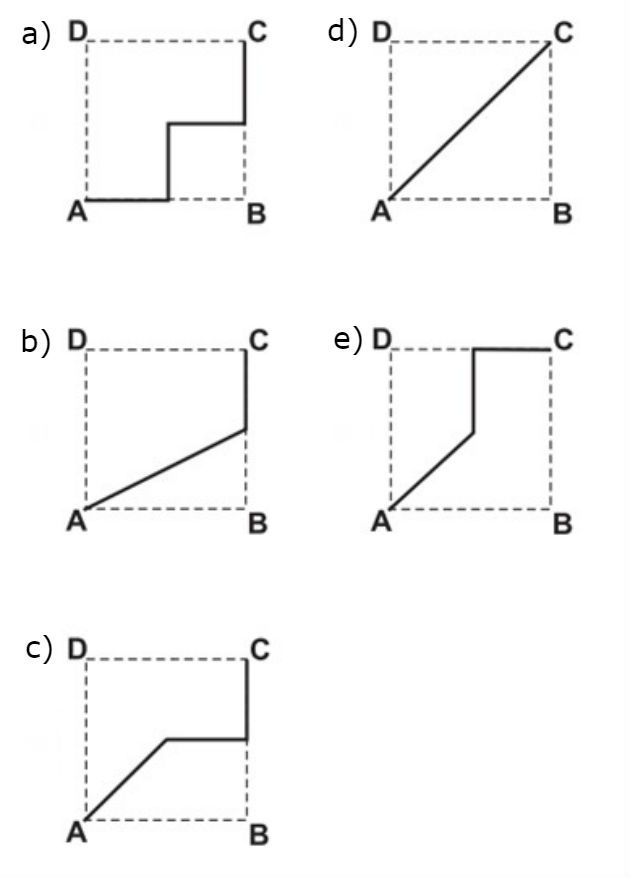
Quem pratica mais, acerta mais! Ganhe acesso a mais 9 questões exclusivas e turbine sua preparação com o Toda Matéria Plus!
Questão 11
Quatro suspeitos de praticar um crime fazem as seguintes declarações:
- João: Carlos é o criminoso
Confira nosso teste de raciocínio lógico.
Pratique exercícios sobre tabela-verdade.
Você também pode se interessar por:
- O que é lógica?
- Método Dedutivo: conceito, exemplo e método indutivo
- Desafios matemáticos
- Quiz de matemática
- Exercícios de Probabilidade
- Conjuntos Numéricos
- Exercícios de Porcentagem
- Exercícios de Análise Combinatória
Questões para OBMEP (Olimpíada de Matemática):
- Questões para Olimpíada Mirim 1 OBMEP.
- Questões para Olimpíada Mirim 2 OBMEP
- Questões para Olimpíada de Matemática - OBMEP Nível 1
- Questões para Olimpíada de Matemática - OBMEP Nível 2
- Questões para Olimpíada de Matemática Nível 3 (ensino médio)
ASTH, Rafael. Exercícios de Raciocínio Lógico (questões com respostas). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/raciocinio-logico-exercicios/. Acesso em:





