Exercícios de Porcentagem
A porcentagem (símbolo %) é uma razão cujo denominador é igual a 100. Ela representa uma comparação de uma parte com o todo.
Questões nível fácil
Questão 1
25 representa quantos por cento de 200?
a) 12,5%
b) 15,5%
c) 16%
d) 20%
Alternativa correta: a) 12,5%.
Para determinar a porcentagem, basta dividir 25 por 200.
Agora, multiplicamos o resultado por 100.
Portanto, 25 representa 12,5% de 200.
Questão 2
30 representa 15% de qual número?
a) 150
b) 200
c) 350
d) 400
Alternativa correta: b) 200.
Para resolver esse problema podemos utilizar a regra de três.
O todo, que corresponde ao número que queremos descobrir, vale 100%.
Portanto, 30 representa 15% de 200.
Questão 3
Em uma sala de aula há 30 alunos, dos quais 40% são meninas. Quantas meninas têm na sala?
a) 10 meninas
b) 12 meninas
c) 15 meninas
d) 18 meninas
Alternativa correta: b) 12 meninas.
Utilizando a regra de três encontramos a quantidade de meninas na sala.
Portanto, em uma sala de 30 alunos há 12 meninas.
Questão 4
Convertendo a fração em uma fração centesimal, qual o resultado em porcentagem?
a) 10%
b) 20%
c) 30%
d) 40%
Alternativa correta: d) 40%.
A fração centesimal possui como denominador o número 100 e é representada dessa forma:
Para converter em uma fração centesimal precisamos descobrir o valor de x.
Para descobrir o valor de x, multiplicamos em cruz.
Portanto, a razão centesimal é e representa 40%.
Questão 5
Júlia acertou 75% das questões de Matemática do teste e Mariana acertou 4/5. Quem acertou mais questões?
a) Júlia
b) Mariana
c) As duas acertaram o mesmo número de questões.
Alternativa correta: b) Mariana.
Para comparar a porcentagem de acertos de Júlia e Mariana precisamos converter 4/5 em uma razão centesimal e, depois, encontrar a porcentagem.
Fazendo a multiplicação em cruz, temos:
Portanto, a fração centesimal é , que corresponde a 80%. Com esse resultado, chegamos a conclusão que Mariana foi quem acertou mais questões.
Questão 6
Para as frações irredutíveis abaixo, determine as porcentagens correspondentes.
a) 1/5
b) 4/5
c) 9/20
Questão 7
Para cada uma das frações apresentadas a seguir, complete o quadro com as informações pedidas.
| Porcentagem | 5% | 27% | 32% | 130% |
|---|---|---|---|---|
| Leitura | ||||
| Fração | ||||
| Número decimal |
Questão 8
Na promoção de uma loja de eletrodomésticos, um aparelho de som que custava R$ 400,00 teve um desconto de 12%. Quanto o cliente que decidir comprar o equipamento pagará?
a) R$ 372,00
b) R$ 342,00
c) R$ 362,00
d) R$ 352,00
Alternativa correta: d) R$ 352,00.
Para descobrir o desconto concedido, devemos calcular quanto é 12% de 400,00 realizando a seguinte operação:
Subtraindo o desconto calculado do valor total do aparelho de som, temos o valor final pago pelo cliente.
R$ 400,00 - R$ 48,00 = R$ 352,00
Questão 9
Observe a figura abaixo e responda: a fração do desenho que não está pintada corresponde a que porcentagem?
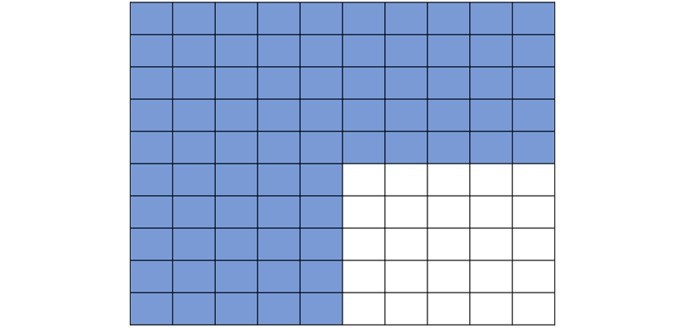
a) 20%
b) 30%
c) 25%
d) 35%
Alternativa correta: c) 25%.
Podemos ver que a figura é um quadrado 10x10, pois há 10 quadradinhos no comprimento e 10 quadradinhos de altura. Portanto, a figura é formada por 100 quadradinhos.
Observe que podemos então dividi-la em 4 partes iguais de 25 quadradinhos.
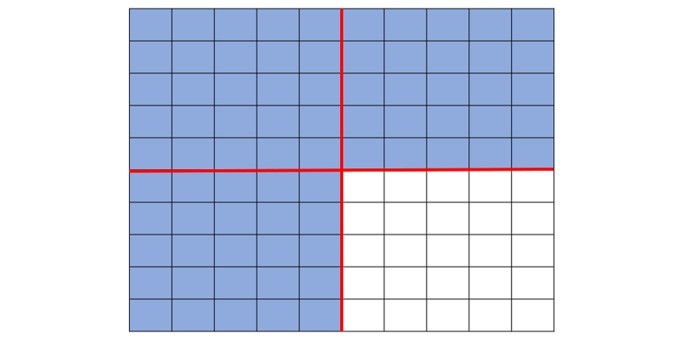
Destas quatro partes, apenas uma não está pintada, ou seja, 1/4 da figura.
Para transformar 1/4 em uma fração centesimal podemos multiplicar o numerador e o denominador por 25.
Portanto, a porcentagem que corresponde a parte não pintada é 25% (lê-se vinte e cinco por cento).
Questões nível médio
Questão 10
Em um concurso, 520 candidatos se inscreveram. No dia da prova apenas 364 candidatos compareceram. Neste caso, qual foi a porcentagem dos candidatos que faltaram a prova?
a) 10%
b) 20%
c) 30%
d) 40%
Alternativa correta: c) 30%.
Como estamos interessados em saber a porcentagem dos candidatos que faltaram, primeiro vamos encontrar o número de faltosos. Assim, temos:
520 - 364 = 156
Agora, precisamos calcular quantos por cento representa esse valor. Para isso, vamos escrever a razão entre o número de faltosos e o número total de inscritos. Temos então:
Assim, 30% dos candidatos faltaram a prova.
Questão 11
Em uma indústria, o setor de qualidade constatou que um lote com 4500 peças, 180 apresentavam algum defeito. Para um lote ser aprovado é necessário que o número de peças com defeito seja inferior a 3%. Neste caso, o lote foi aprovado ou reprovado?
a) Aprovado com 1% de peças com defeito.
b) Aprovado com 2% de peças com defeito.
c) Reprovado com 3% de peças com defeito.
d) Reprovado com 4% de peças com defeito.
Alternativa correta: d) Reprovado com 4% de peças com defeito.
O lote foi reprovado, pois apresenta 4% das peças com defeito, que é superior ao valor aceitável (3%).
Questão 12
Na última liquidação de verão, uma loja vendia todos os seus produtos com um desconto de 15%. Se uma camisa antes da liquidação custava R$ 145,00, quanto passou a custar na liquidação?
a) R$ 112,20
b) R$ 123,25
c) R$ 135,50
d) R$ 140,15
Alternativa correta: b) R$ 123,25.
Para resolver o exercício devemos calcular quanto custa o desconto em reais. Assim, vamos calcular 15% de R$145. Esse cálculo é feito passando a porcentagem para fração ou para número decimal e depois multiplicando o valor por 145.
Assim, temos:
Multiplicando 145 por 0,15 encontramos 21,75 e esse será o valor em reais do desconto. Para encontrar o valor da camisa na liquidação, devemos diminuir o valor do desconto do valor antes da liquidação.
Desta forma, na liquidação a camisa passou a custar R$ 123,25.
Esse problema poderia também ser feito da seguinte maneira:
Com o desconto de 15% o preço da camisa passou a representar 85% do preço antes da liquidação (100% - 15%). Como:
Calculando:
Onde encontramos o mesmo valor anterior.
Questão 13
Os vendedores de uma loja recebem mensalmente um salário fixo no valor de R$ 1200,00 e uma comissão de 6% referente ao valor total do que venderam no mês. Sendo assim, qual será o valor recebido por um vendedor que vendeu no mês R$ 14000,00?
a) R$ 2040,00
b) R$ 2080,00
c) R$ 3020,00
d) R$ 3040,00
Alternativa correta: a) R$ 2040,00.
O vendedor receberá de comissão R$ 840,00, mais o salário de R$ 1200,00. Assim, ele receberá o valor total de R$ 2040,00.
1º passo: calcular a comissão recebida pelo vendedor.
2º passo: Calcular o valor total recebido pelo vendedor.
Questão 14
Em uma loja, uma máquina de lavar roupas custava R$ 1500,00 e seu preço sofreu um aumento de 3%. Logo após o aumento a loja resolveu fazer uma promoção oferecendo um desconto de 3% no mesmo produto. Qual o valor do produto após o aumento e após o desconto?
a) R$ 1555,00 com aumento e R$ 1498,65 com desconto.
b) R$ 1545,00 com aumento e R$ 1500,00 com desconto.
c) R$ 1545,00 com aumento e R$ 1498,65 com desconto.
d) R$ 1555,00 com aumento e R$ 1500,00 com desconto.
Alternativa correta: c) R$ 1545,00 com aumento e R$ 1498,65 com desconto.
1º passo: Calcular o aumento correspondente aos 3%.
Sendo assim, o aumento sofrido pela máquina foi de R$ 45,00 e seu valor passou a ser R$ 1545,00.
2º passo: Calcular o desconto correspondente aos 3%.
A máquina passou a custar R$ 1498,65.
Com o aumento a máquina passou a custar R$ 1545,00. Depois do desconto ela passou a custar R$ 1498,65, logo a máquina não voltou ao valor inicial.
Questão 15
Com base nas informações que constam no gráfico abaixo, responda:
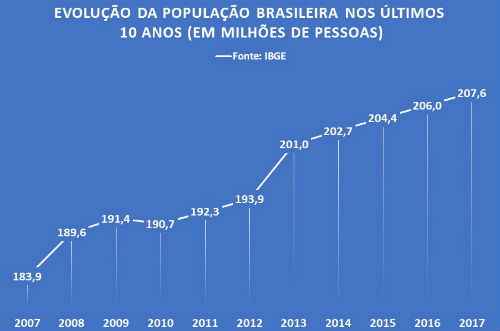
a) Qual foi o aumento percentual da população brasileira nos últimos 10 anos?
b) Em qual período houve uma redução no número de brasileiros?
c) Neste período, essa redução representou quanto porcento?
Questões de porcentagem no Enem
Questão 16
(Enem/2015) Segundo dados apurados no Censo 2010, para uma população de 101,8 milhões de brasileiros com 10 anos ou mais de idade e que teve algum tipo de rendimento em 2010, a renda média mensal apurada foi de R$1202,00. A soma dos rendimentos mensais dos 10% mais pobres correspondeu a apenas 1,1% do total de rendimentos dessa população considerada, enquanto que a soma dos rendimentos mensais dos 10% mais ricos correspondeu a 44,5% desse total.
Qual foi a diferença, em reais, entre a renda média mensal de um brasileiro que estava na faixa dos 10% mais ricos e de um brasileiro que estava na faixa dos 10% mais pobres?
a) 240,40
b) 548,11
c) 1 723,67
d) 4 026,70
e) 5 216,68
Alternativa correta: e) 5 216,68.
Para facilitar os cálculos, vamos utilizar as seguintes abreviações:
renda média mensal: R
população total: P
valor recebido: V
Vamos iniciar com a renda dos mais pobres.
Segundo o enunciado, a soma dos rendimentos mensais dos 10% mais pobres correspondeu a apenas 1,1% do total de rendimentos da população considerada, ou seja,
1,1% . R . P = V . 10%.P
1,1% . 1202,00 . P = V . 10%.P
V = 1,1% . 1202,00 . P/10%.P
V = 1,1% . 1202,00/10%
V = R$ 132,22
Agora, calculamos a renda dos mais ricos.
Segundo o enunciado, a soma dos rendimentos mensais dos 10% mais ricos correspondeu a 44,5% do total de rendimentos da população considerada, ou seja,
44,5% . R . P = V . 10%.P
44,5% . 1202,00 . P = V . 10%.P
V = 44,5% . 1202,00 . P/10%.P
V = 44,5% . 1202,00/10%
V = R$ 5.348,90
Portanto, a diferença a diferença, em reais, entre a renda média mensal de um brasileiro que estava na faixa dos 10% mais ricos e de um brasileiro que estava na faixa dos 10% mais pobres é:
R$ 5.348,90 - R$ 132,22 = R$ 5216,68 reais, conforme a letra “e”.
Questão 17
Leia também: Porcentagem: o que é e como calcular (com exemplos e exercícios)
ASTH, Rafael. Exercícios de Porcentagem. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-de-porcentagem/. Acesso em:



