Porcentagem
A Porcentagem ou Percentagem representa uma razão cujo denominador é igual a 100 e indica uma comparação de uma parte com o todo.
O símbolo % é usado para designar a porcentagem. Um valor em porcentagem, pode ainda ser expresso na forma de fração centesimal (denominador igual a 100) ou como um número decimal.
Exemplo:
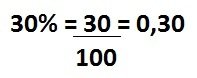
Para facilitar o entendimento, veja a tabela abaixo:
| Porcentagem | Razão Centesimal | Número Decimal |
|---|---|---|
| 1% | 1/100 | 0,01 |
| 5% | 5/100 | 0,05 |
| 10% | 10/100 | 0,1 |
| 120% | 120/100 | 1,2 |
| 250% | 250/100 | 2,5 |
Saiba mais sobre as Frações.
Como Calcular a Porcentagem?
Podemos utilizar diversas formas para calcular a porcentagem. Abaixo apresentamos três formas distintas:
- regra de três
- transformação da porcentagem em fração com denominador igual a 100
- transformação da porcentagem em número decimal
Devemos escolher a forma mais adequada conforme o problema que queremos resolver.
Exemplo 1:
Calcule 30% de 90
Para usar a regra de três no problema, vamos considerar que 90 corresponde ao todo, ou seja, 100%. O valor que queremos encontrar chamaremos x. A regra de três será expressa como:
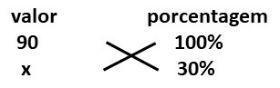
Para resolver usando frações, primeiro temos que transformar a porcentagem em uma fração com denominador igual a 100:
Podemos ainda transformar a porcentagem em número decimal:
30% = 0,3
0,3 . 90 = 27
O resultado é o mesmo nas três formas, ou seja, 30% de 90 corresponde a 27.
Exemplo 2:
90 corresponde a 30% de qual valor?
Note que nesse exemplo, já conhecemos o resultado da porcentagem e queremos conhecer o valor que corresponde ao todo (100%).
Usando a regra de três, temos:
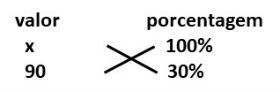
Podemos ainda resolver o problema transformando a porcentagem em número decimal:
30% = 0,3
Então é só resolver a seguinte equação:
Assim, 30% de 300 é igual a 90.
3) 90 corresponde a quanto por cento de 360?
Podemos resolver esse problema escrevendo na forma de fração:
Ou ainda, podemos resolver usando regra de três:

Desta forma, 90 corresponde a 25% de 360.
Veja também: como calcular porcentagem?
Exercícios Resolvidos
Exercício 1
Calcule os valores abaixo:
a) 6% de 100
b) 70% de 100
c) 30% de 50
d) 20 % de 60
e) 25% de 200
f) 7,5% de 400
g) 42% de 300
h) 10% de 62,5
i) 0,1% de 350
j) 0,5% de 6000
Exercício 2
(ENEM-2013) Para aumentar as vendas no início do ano, uma loja de departamentos remarcou os preços de seus produtos 20% abaixo do preço original. Quando chegam ao caixa, os clientes que possuem o cartão fidelidade da loja têm direito a um desconto adicional de 10% sobre o valor total de suas compras.
Um cliente deseja comprar um produto que custava R$50,00 antes da remarcação de preços. Ele não possui o cartão fidelidade da loja. Caso esse cliente possuísse o cartão fidelidade da loja, a economia adicional que obteria ao efetuar a compra, em reais, seria de:
a) 15,00
b) 14,00
c) 10,00
d) 5,00
e) 4,00
Saiba mais:
- Exercícios de Regra de Três
- Matemática Financeira
- Exercícios de matemática financeira
- Exercícios de Juros Simples
ASTH, Rafael. Porcentagem. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/porcentagem/. Acesso em:


