Juros Simples e Compostos

Rafael C. Asth

Professor de Matemática e Física

Os juros simples e compostos são cálculos efetuados com o objetivo de corrigir os valores envolvidos nas transações financeiras, isto é, a correção que se faz ao emprestar ou aplicar uma determinada quantia durante um período de tempo.

O valor pago ou resgatado dependerá da taxa cobrada pela operação e do período que o dinheiro ficará emprestado ou aplicado. Quanto maior a taxa e o tempo, maior será este valor.

Diferença entre juros simples e compostos

Nos juros simples a correção é aplicada a cada período e considera apenas o valor inicial. Nos juros compostos a correção é feita em cima de valores já corrigidos.

Por isso, os juros compostos também são chamados de juros sobre juros, ou seja, o valor é corrigido sobre um valor que já foi corrigido.

Sendo assim, para períodos maiores de aplicação ou empréstimo a correção por juros compostos fará com que o valor final a ser recebido ou pago seja maior que o valor obtido com juros simples.

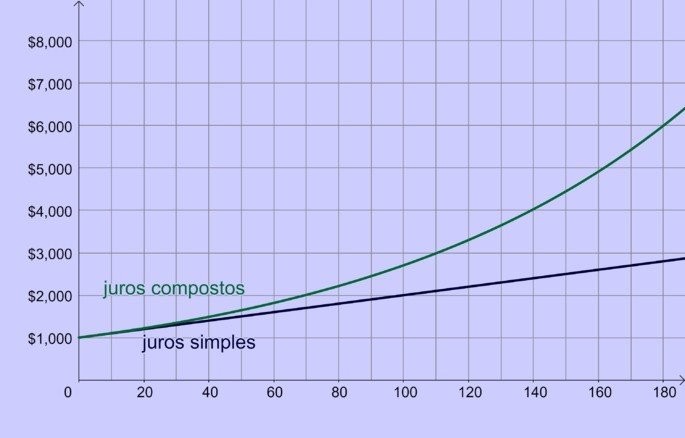
A maioria das operações financeiras utiliza a correção pelo sistema de juros compostos. Os juros simples se restringem as operações de curto período.

Fórmula de juros simples

Os juros simples são calculados aplicando a seguinte fórmula:

Sendo,

J: juros
C: valor inicial da transação, chamado em matemática financeira de capital
i: taxa de juros (valor normalmente expresso em porcentagem)
t: período da transação

Podemos ainda calcular o valor total que será resgatado (no caso de uma aplicação) ou o valor a ser quitado (no caso de um empréstimo) ao final de um período predeterminado.

Esse valor, chamado de montante, é igual a soma do capital com os juros, ou seja:

Podemos substituir o valor de J, na fórmula acima e encontrar a seguinte expressão para o montante:

A fórmula que encontramos é uma função afim, desta forma, o valor do montante cresce linearmente em função do tempo.

Exemplo

Se o capital de R$ 1 000,00 rende mensalmente R$ 25,00, qual é a taxa anual de juros no sistema de juros simples?

Solução

Primeiro, vamos identificar cada grandeza indicada no problema.

C = R$ 1 000,00
J = R$ 25,00
t = 1 mês
i = ?

Agora que fizemos a identificação de todas as grandezas, podemos substituir na fórmula dos juros:

Entretanto, observe que essa taxa é mensal, pois usamos o período de 1 mês. Para encontrar a taxa anual precisamos multiplicar esse valor por 12, assim temos:

i = 2,5.12= 30% ao ano

Fórmula de juros compostos

O montante capitalizado a juros compostos é encontrado aplicando a seguinte fórmula:

Sendo,

M: montante
C: capital
i: taxa de juros
t: período de tempo

Diferente dos juros simples, neste tipo de capitalização, a fórmula para o cálculo do montante envolve uma variação exponencial. Daí se explica que o valor final aumente consideravelmente para períodos maiores.

Exemplo

Calcule o montante produzido por R$ 2 000,00 aplicado à taxa de 4% ao trimestre, após um ano, no sistema de juros compostos.

Solução

Identificando as informações dadas, temos:

C = 2 000
i = 4% ou 0,04 ao trimestre
t = 1 ano = 4 trimestres
M = ?

Substituindo esses valores na fórmula de juros compostos, temos:

Observação: o resultado será tão melhor aproximado quanto o número de casas decimais utilizadas na potência.

Portanto, ao final de um ano o montante será igual a R$ 2 339,71.

Aprenda mais com exercícios de matemática financeira.

Exercícios Resolvidos

Questão 1

Cálculo do montante

Qual o montante de uma aplicação de R$500,00, a uma taxa de 3% ao mês, em um período de 1 ano e 6 meses, nos sistemas de juros simples e compostos?

Juros simples

Juros compostos

Questão 2

Cálculo do capital

Um certo capital foi aplicado por um período de 6 meses. A taxa foi de 5% ao mês. Após esse período, o montante era de R$5000,00. Determine o capital.

Juros simples

Ver Resposta

Colocando C em evidência na fórmula de juros simples:

M = C + J

M = C + C.i.t

M = C(1+i.t)

Isolando C na equação:

Juros compostos

Questão 3

Cálculo da taxa de juros

Qual seria a taxa mensal de juros de um investimento de R$1000,00 em um período de oito meses que obteve um montante de R$1600,00.

Juros simples

Juros compostos

Questão 4

Cálculo do período da aplicação (tempo)

Um capital de R$8000,00 foi investido a juro mensal de 9%, obtendo um montante de R$10360,00.

Quanto tempo esse capital ficou investido?

Juros simples

Juros compostos

Ver Resposta

Nesta etapa, nos deparamos com uma equação exponencial.

Para resolvê-la, iremos utilizar o logaritmo, aplicando um logaritmo de mesma base, nos dois lados da equação.

Usando uma propriedade dos logaritmos no lado direito da equação, temos:

Questão 5

UECE - 2018

Uma loja vende um aparelho de TV, com a seguintes condições de pagamento: entrada no valor de R$ 800,00 e um pagamento de R$ 450,00 dois meses depois. Se o preço do televisor à vista é de R$1.200,00, então, a taxa de juros simples mensal embutida no pagamento é
A) 6,25%.
B) 7,05%.
C) 6,40%.
D) 6,90%.

Você pode se interessar por mais exercícios de juros simples fáceis (resolvidos).

Equivalência de capitais

Em Matemática financeira é fundamental termos em mente que as quantias envolvidas em uma transação serão deslocadas no tempo.

Diante deste fato, fazer uma análise financeira implica comparar valores presentes com os valores futuros. Assim, devemos ter uma forma de fazer a equivalência de capitais em diferentes momentos.

Quando calculamos o montante, na fórmula de juros compostos, estamos encontrando o valor futuro para t períodos de tempo, segundo uma taxa i, a partir de um valor presente.

Isto é feito através da multiplicação do termo (1+i)ⁿ pelo valor presente, ou seja:

Ao contrário, se quisermos encontrar o valor presente conhecendo o valor futuro, iremos fazer uma divisão, isto é:

Exemplo:

Para comprar uma moto aproveitando um ótimo preço, uma pessoa pediu um empréstimo de R$ 6 000,00 a uma financeira a juros mensais de 15%. Dois meses depois, pagou R$ 3 000,00 e liquidou a dívida no mês seguinte.

Qual foi o valor da última prestação pago pela pessoa?

Solução

Se a pessoa conseguiu liquidar o valor devido pelo empréstimo, então o valor pago na primeira parcela mais a segunda parcela são iguais ao valor devido.

Entretanto, as parcelas foram corrigidas ao longo do período por juros mensais. Sendo assim, para igualar essas quantias temos que conhecer seus valores equivalentes em uma mesma data.

Iremos fazer a equivalência considerando o momento do empréstimo, conforme o esquema abaixo:

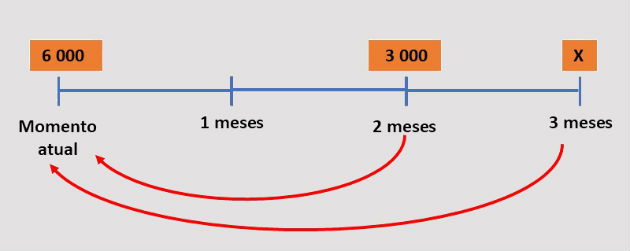
Usando a fórmula para dois e três meses:

Portanto, o último pagamento efetuado foi de R$ 5 675,25.

Exercício resolvido

Questão 6

Um empréstimo foi feito à taxa mensal de i%, usando juros compostos, em oito parcelas fixas iguais a P.

O devedor tem a possibilidade de quitar a dívida antecipadamente a qualquer momento, pagando para isso o valor atual das parcelas ainda a pagar. Após pagar a 5ª parcela, resolve quitar a dívida no ato de pagar a 6ª parcela.

A expressão que corresponde ao valor total pago pela quitação do empréstimo é:

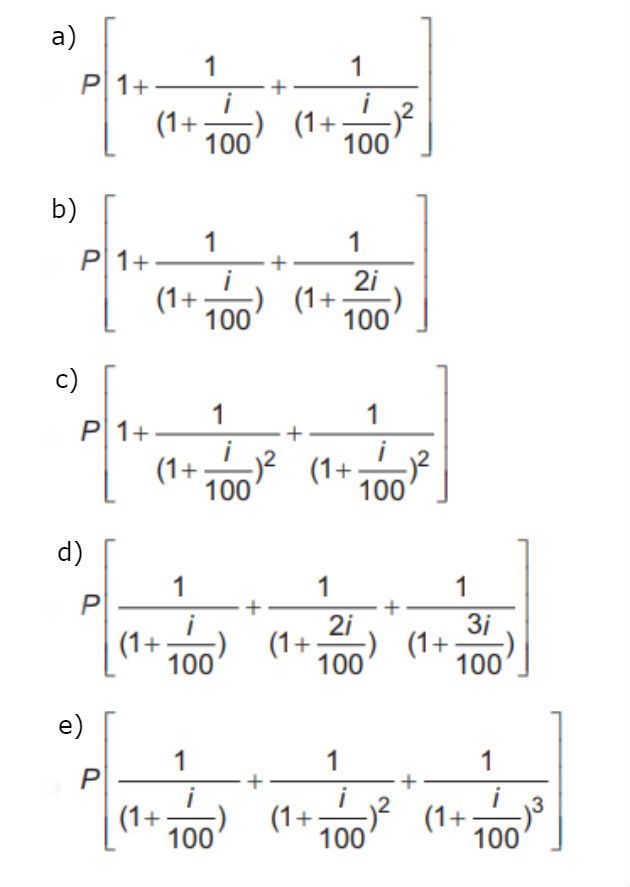
Aprenda mais com:

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.