Fórmula de Bhaskara

A fórmula de Bhaskara é usada para resolver as equações de segundo grau, também conhecidas como equações quadráticas. Resolver a equação é determinar suas raízes e, para isso, utiliza-se a fórmula de Bhaskara como método prático.

Por meio de um passo a passo que inclui uma sequência de operações, a fórmula de Bhaskara permite determinar os valores da incógnita x que zeram a equação. Estes valores são chamados de raízes da equação.

A Fórmula de Bhaskara é expressa como:

Na fórmula, x é o valor pretendido, a raiz da equação, já as letras a, b e c são números reais, obtidos da equação do segundo grau que será resolvida.

Uma equação polinomial do segundo grau tem a forma:

Onde,

x: é uma variável chamada de incógnita.
a: coeficiente quadrático (o número que multiplica o x²).
b: coeficiente linear (o número que multiplica o x).
c: coeficiente constante (o número que aparece se nenhum x).

Uma equação do segundo grau possui, no máximo, duas raízes.

Fórmula do delta ()

A expressão na raiz quadrada na fórmula de Bhaskara é chamada discriminante da equação sendo representada pela letra grega delta (Δ), ou seja:

Normalmente essa expressão é calculada separadamente, pois conforme o valor encontrado, podemos saber antecipadamente o número de raízes da equação e se pertencem ao conjunto dos números reais.

Note que a, b e c são as constantes da equação e o valor de Delta (Δ) pode ocorrer de três maneiras:

Se o valor de Δ for maior que zero (Δ > 0), a equação terá duas raízes reais e distintas.

Se o valor de Δ for igual a zero (Δ = 0), a equação apresentará uma raiz real.

Se o valor de Δ for menor que zero (Δ<0), a equação não possui raízes reais.

Assim, substituindo a expressão do discriminante por delta, a fórmula de Bhaskara ficará:

Exemplo de uso da fórmula de Bhaskara

Quantas e quais são as raízes da equação ?

Resolução

O primeiro passo para resolver uma equação usando a fórmula de Bhaskara é identificar os coeficientes da equação. Desta forma, os coeficientes na equação são:

a = + 1
b = - 5
c = + 6.

Para saber o número de raízes, precisamos calcular o valor do delta, assim temos:

Como delta é maior que zero , então a equação terá duas raízes reais e distintas. Vamos agora aplicar a fórmula de Bhaskara para encontrar o valor das raízes.

Lembre-se que uma raiz quadrada tem duas respostas, uma positiva e uma negativa, por isso, repetimos o cálculo com a fórmula de Bhaskara, utilizando o valor positivo e negativo.

Assim, as duas raízes da equação são 2 e 3.

Leia mais em Função Quadrática.

Classificações das Equações de Segundo Grau

As equações do 2º grau podem ser de dois tipos:

• Completas: quando os coeficientes a, b e c, são diferentes de zero.
• Incompletas: quando o coeficiente a é diferente de zero (a ≠ 0) e b, ou c, ou ambos são iguais a zero.

A fórmula de Bhaskara é mais utilizada nas equações de segundo grau completas. Nas incompletas também pode ser usada, entretanto, existem métodos mais simples para resolvê-las.

Função do segundo grau e fórmula de Bhaskara

As funções do segundo grau são determinadas por polinômios do segundo grau.

Esta função tem o domínio real (eixo x) e sua imagem está determinada no intervalo que vai do vértice ao infinito, [vértice, infinito).

O gráfico da função do segundo grau é uma parábola e pode ter concavidade para cima (se o coeficiente a, que multiplica o termo x² é positivo, ou para baixo quando a é negativo.

Os pontos de intersecção entre a curva da função e o eixo x são as raízes determinadas pela fórmula de Bhaskara.

Exemplo
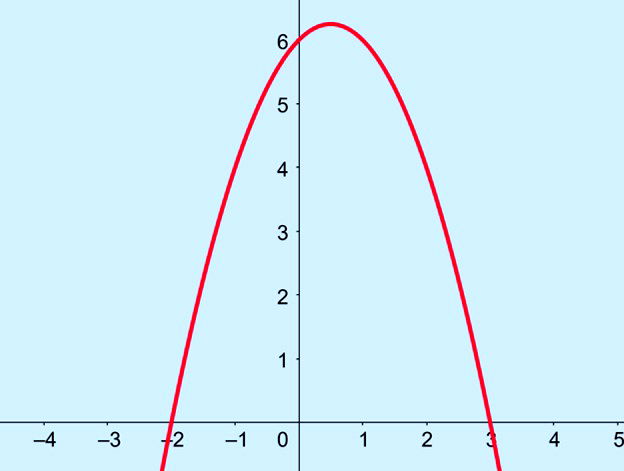
Esboce em um plano cartesiano a curva da função do 2° grau:

Resolução:
Como o parâmetro a que multiplica o termo x² é negativo, no caso a = -1, a parábola é aberta para baixo, possui concavidade para baixo.

Para conhecer os pontos onde a curva corta o eixo x, temos que determinar as raízes da equação do segundo grau. Para isso, igualamos a função à 0.

Determinando as raízes.

Os coeficientes são:

a = -1
b = 1
c = 6

Delta ou discriminante:

Utilizando a fórmula de Bhaskara e considerando os valores positivos e negativos da raiz quadrada:

As raízes da equação são -2 e 3, dessa forma, a curva cortará o eixo x nestes pontos.

Plotando o gráfico da função temos:

Curiosidade

A fórmula de Bhaskara recebe esse nome uma vez que faz homenagem ao matemático e astrônomo indiano Bhaskara Akaria ou Bhakara II (1114-1185). Ele é considerado um dos mais importantes matemáticos do século XII.

Exercícios de Fórmula de Bhaskara

Exercício 1

Determine as raízes da equação .

Exercício 2

(PUC- Campinas) Se v e w são as raízes da equação x² + ax + b = 0, em que a e b são coeficientes reais, então v² + w² é igual a:

a) a² - 2b
b) a² + 2b
c) a² – 2b²
d) a² + 2b²
e) a² – b2

Pratique mais exercícios sobre fórmula de Bhaskara.