Energia Cinética: definição, fórmulas e exercícios

Revisão por Rafael C. Asth

Professor de Matemática e Física

A energia cinética é a energia associada ao movimento dos corpos. Do grego o termo "cinética" significa "movimento".

Qualquer corpo em movimento é capaz de realizar trabalho, portanto, possui energia, que neste caso é chamada de cinética.

A unidade da energia cinética, no sistema internacional, é medida em Joule (J), em homenagem ao cientista inglês James Prescott Joule (1818-1889).

Fórmula da Energia Cinética

Para calcular a energia cinética dos corpos, utiliza-se a equação abaixo:

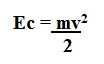
Energia Cinética

Onde:

E_c: energia cinética, também pode ser representada pela letra K (J)
m: massa do corpo (kg)
v: velocidade do corpo (m/s)

A partir disso, conclui-se que se duplicarmos a massa de um corpo, mantendo sua velocidade, a sua energia cinética também irá duplicar.

Por outro lado, a velocidade está elevada ao quadrado, então se o seu valor duplicar e sua massa permanecer constante, a energia cinética será quadruplicada.

Exemplo

Qual a energia cinética de uma pessoa com 60 kg se movendo numa velocidade de 10 m/s?

$reto E com reto c subscrito igual a numerador reto m. reto v ao quadrado sobre denominador 2 fim da fração reto E com reto c subscrito igual a numerador 60.10 ao quadrado sobre denominador 2 fim da fração igual a numerador 60.100 sobre denominador 2 fim da fração igual a 3 espaço 000 espaço reto J espaço$

Assim, no instante considerado, a energia cinética do corpo é igual a 3000 J.

Teorema da Energia Cinética

Para um corpo sofrer variação na sua velocidade, é necessário que um trabalho seja realizado sobre ele. Essa variação na velocidade do corpo faz com que sua energia cinética varie.

O teorema da energia cinética indica que a variação da energia cinética é igual ao trabalho, ou seja:

$começar estilo tamanho matemático 18px reto T espaço igual a espaço incremento Ec fim do estilo$

Onde,

T: trabalho (J)
∆E_c: variação da energia cinética (J)

Exemplo

Qual o trabalho que deverá ser realizado sobre um corpo de massa igual a 6 kg, para que sua velocidade passe de 4 m/s para 20 m/s?

Solução

O trabalho é igual a variação da energia cinética. Essa variação pode ser calculada diminuindo-se o valor da energia cinética final da energia cinética inicial:

$incremento Ec espaço igual a espaço Ec com final subscrito espaço menos espaço Ec com inicial subscrito$

Calculando os valores de E_cfe E_ci, temos:

$começar estilo tamanho matemático 14px reto E com cf subscrito igual a numerador 6.20 ao quadrado sobre denominador 2 fim da fração igual a 1200 espaço reto J reto E com ci subscrito igual a numerador 6.4 ao quadrado sobre denominador 2 fim da fração igual a 48 espaço reto J incremento reto E com reto c subscrito igual a 1200 menos 48 igual a 1152 espaço reto J reto T igual a incremento reto E com reto c subscrito igual a 1152 espaço reto J fim do estilo$

Portanto, o trabalho necessário para mudar a velocidade do corpo, será igual a 1152 J.

Energia cinética e Energia Potencial

A soma da energia cinética, produzida pelo movimento, e da energia potencial, gerada pela interação e posicionamento dos corpos em relação a um referencial, correspondem à energia mecânica.

A energia mecânica (E_m) é expressa matematicamente como a soma da energia cinética (E_c) e energia potencial (E_p).

$começar estilo tamanho matemático 18px Em espaço igual a espaço Ec espaço mais espaço Ep fim do estilo$

As fórmulas para calcular a energia cinética e a energia potencial são:

Energia Cinética:

$Ec espaço igual a espaço mv ao quadrado sobre 2$

Energia potencial elástica:

$Epe igual a espaço kx ao quadrado sobre 2$

Energia potencial gravitacional:

$Epg igual a espaço reto m. espaço reto g. espaço reto h$

Onde,

m: massa (kg)
v: velocidade (m/s)
K: constante elástica (N/m)
x: deformação (m)
g: aceleração da gravidade de aproximadamente 10 m/s²
h: altura (m)

Pela conversão de unidades, temos:

$1 espaço reto J espaço igual a espaço 1 espaço reto N. reto m espaço igual a espaço 1 espaço numerador kg. reto m sobre denominador reto s ao quadrado fim da fração reto m igual a 1 numerador kg. reto m ao quadrado sobre denominador reto s ao quadrado fim da fração$

Saiba mais sobre:

Exercícios Resolvidos sobre Energia Cinética

Questão 1

Se uma bola de massa 0,5 kg é arremessada e atinge uma velocidade de 7 m/s, qual a sua energia cinética durante o movimento?

Ver Resposta

Resposta correta: 12,25 J.

A energia cinética é calculada através da seguinte fórmula:

$reto E com reto c subscrito igual a numerador reto m. reto v ao quadrado sobre denominador 2 fim da fração$

Substituindo os dados da questão na fórmula acima, encontramos a energia cinética, temos:

$reto E com reto c subscrito igual a numerador 0 vírgula 5.7 ao quadrado sobre denominador 2 fim da fração igual a numerador 0 vírgula 5.49 sobre denominador 2 fim da fração igual a 12 vírgula 25 espaço reto J espaço$

Portanto, a energia cinética adquira pela bola é de 12,25 J.

Questão 2

(Fuvest - 2017) Helena, cuja massa é 50 kg, pratica o esporte radical bungee jumping. Em um treino, ela se solta da beirada de um viaduto, com velocidade inicial nula, presa a uma faixa elástica de comprimento natural L₀ = 15 m e constante elástica k = 250 N/m. Quando a faixa está esticada 10 m além de seu comprimento natural, o módulo da velocidade de Helena é: (Note e adote: Aceleração da gravidade: 10 m/s² . A faixa é perfeitamente elástica; sua massa e efeitos dissipativos devem ser ignorado )

a) 0 m/s
b) 5 m/s
c) 10 m/s
d) 15 m/s
e) 20 m/s

Ver Resposta

Alternativa correta: a) 0 m/s.

Para calcular a velocidade de Helena quando a faixa está esticada 10 m, podemos utilizar o teorema da energia cinética.

Como Helena está presa em uma faixa elástica, podemos calcular o trabalho da força elástica e ao se soltar do viaduto, teremos também o trabalho da força peso.

Desta forma, o trabalho total produzido será igual a variação da energia cinética sofrida por Helena.

Sendo o trabalho total igual a soma do trabalho da força peso com o trabalho da força elástica.

$começar estilo tamanho matemático 14px T com T subscrito itálico igual a itálico incremento E com c subscrito T com P subscrito itálico mais T com e l a s subscrito fim do subscrito itálico igual a itálico incremento E com c subscrito fim do estilo$

Assim, vamos começar calculando o valor do trabalho da força peso.

O comprimento natural da faixa é 15 m, entretanto, ela está esticada 10 m. Portanto, a distância percorrida por Helena foi de 25 m (15 + 10).

Considerando que o trabalho da força peso na descida é positivo, temos:

$começar estilo tamanho matemático 14px T com P subscrito itálico espaço itálico igual a itálico espaço m itálico espaço itálico. itálico espaço g itálico espaço itálico. itálico espaço h itálico espaço itálico igual a itálico 50 itálico espaço itálico. itálico espaço itálico 10 itálico espaço itálico. itálico espaço itálico 25 itálico espaço itálico igual a itálico espaço itálico 12 itálico espaço itálico 500 itálico espaço J fim do estilo$

Agora, vamos calcular o trabalho da força elástica.

Perceba que, neste caso, o trabalho será negativo (trabalho resistivo), pois a corda está esticada e a força elástica é contrária ao movimento.

Note ainda que x representa a deformação da faixa. Neste caso, o seu valor é igual a 10 m, assim:

$começar estilo tamanho matemático 14px T com e l a s subscrito fim do subscrito itálico igual a itálico menos numerador k itálico. x à potência de itálico 2 sobre denominador itálico 2 fim da fração itálico igual a itálico menos numerador itálico 250 itálico. itálico 10 à potência de itálico 2 sobre denominador itálico 2 fim da fração itálico igual a itálico menos itálico 12 itálico espaço itálico 500 itálico espaço J fim do estilo$

Como Helena partiu do repouso, sua velocidade inicial era igual a zero. Portanto, sua energia cinética também era igual a zero.

Substituindo os valores encontrados no teorema da energia cinética:

$começar estilo tamanho matemático 14px itálico 12 itálico espaço itálico 500 itálico espaço itálico menos itálico espaço itálico 12 itálico espaço itálico 500 itálico espaço itálico igual a itálico espaço E com c f subscrito fim do subscrito itálico menos itálico 0 E com c f subscrito fim do subscrito itálico igual a itálico 0 itálico seta dupla para a direita v itálico igual a itálico 0 fim do estilo$

Alternativa: a) 0 m/s

Questão 3

(Uerj - 2015) Um carro, em um trecho retilíneo da estrada na qual trafegava, colidiu frontalmente com um poste. O motorista informou um determinado valor para a velocidade de seu veículo no momento do acidente. O perito de uma seguradora apurou, no entanto, que a velocidade correspondia a exatamente o dobro do valor informado pelo motorista.
Considere Ec₁ a energia cinética do veículo calculada com a velocidade informada pelo motorista e Ec₂ aquela calculada com o valor apurado pelo perito.
A razão E_c1/E_c2 corresponde a:

a)) 1/2
b) 1/4
c) 1
d) 2

Ver Resposta

Alternativa correta: b) 1/4.

A razão entre a energia cinética informada pelo motorista e a energia cinética encontrada pelo perito é dada por:

$Error converting from MathML to accessible text.$

Alternativa: b) 1/4

Questão 4

(Enem - 2015) Um carro solar é um veículo que utiliza apenas a energia solar para a sua locomoção. Tipicamente, o carro contém um painel fotovoltaico que converte a energia do Sol em energia elétrica que, por sua vez, alimenta um motor elétrico. A imagem mostra o carro solar Tokai Challenger, desenvolvido na Universidade de Tokai, no Japão, e que venceu o World Solar Challenge de 2009, uma corrida internacional de carros solares, tendo atingido uma velocidade média acima de 100 km/h.

Considere uma região plana onde a insolação (energia solar por unidade de tempo e de área que chega à superfície da Terra) seja de 1 000 W/m² , que o carro solar possua massa de 200 kg e seja construído de forma que o painel fotovoltaico em seu topo tenha uma área de 9,0 m² e rendimento de 30%. Desprezando as forças de resistência do ar, o tempo que esse carro solar levaria, a partir do repouso, para atingir a velocidade de 108 km/h é um valor mais próximo de

a) 1,0 s.
b) 4,0 s.
c) 10 s.
d) 33 s.
e) 300 s.

Ver Resposta

Alternativa correta: d) 33 s.

No carro solar, a energia recebida do Sol é transformada em trabalho. Esse trabalho será igual a variação da energia cinética.

Antes de substituir os valores no teorema da energia cinética, devemos transformar o valor a velocidade para o sistema internacional.

108 km/h : 3,6 = 30 m/s.

O trabalho será igual a:

$começar estilo tamanho matemático 14px T itálico igual a itálico incremento E com c subscrito itálico igual a numerador itálico 200 itálico. itálico 30 à potência de itálico 2 sobre denominador itálico 2 fim da fração itálico menos numerador itálico 200 itálico. itálico 0 à potência de itálico 2 sobre denominador itálico 2 fim da fração itálico igual a itálico 90 itálico espaço itálico 000 itálico espaço J fim do estilo$

No local, a insolação é igual a 1 000 W para cada m² . Como a placa tem uma área de 9 m², a potência do carro será igual a 9 000 W. Entretanto, o rendimento é de 30%, logo a potência útil será igual a 2 700 W.

Lembrando que potência é igual a razão do trabalho pelo tempo, temos:

$começar estilo tamanho matemático 14px P com u subscrito igual a T sobre t seta dupla para a direita 2 espaço 700 igual a numerador 90 espaço 000 sobre denominador t fim da fração seta dupla para a direita t igual a numerador 90 espaço 000 sobre denominador 2 espaço 700 fim da fração seta dupla para a direita t igual a 33 vírgula 3 espaço s fim do estilo$

Alternativa: d) 33 s

Para mais questões com resolução comentada, veja também:

Revisão por Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Edição por Carolina Batista

Bacharela em Química Tecnológica e Industrial pela Universidade Federal de Alagoas (2018) e Técnica em Química pelo Instituto Federal de Educação, Ciência e Tecnologia de Pernambuco (2011).

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações