Energia Potencial

Rafael C. Asth

Professor de Matemática e Física

A energia presente nos corpos dando a eles a capacidade de realizar trabalho é chamada de Energia Potencial.

Quando está relacionada aos trabalhos da força peso, a energia armazenada nos corpos é chamada Energia Potencial Gravitacional e quando está associada a uma força elástica é Energia Potencial Elástica.

A unidade de medida da Energia Potencial é Joule (J).

Energia Potencial Gravitacional

É a energia que um objeto possui devido à sua posição em um campo gravitacional, medida pelo trabalho realizado pelo seu peso para ir de uma posição (mais elevada) à outra (mais abaixo).

Fórmula da energia potencial gravitacional

$começar estilo tamanho matemático 18px reto E com pg espaço subscrito fim do subscrito igual a reto m. reto g. reto h fim do estilo$

Onde,
$começar estilo tamanho matemático 16px reto E com pg espaço subscrito fim do subscrito fim do estilo$ é a energia potencial gravitacional (J);
m é a massa do corpo (kg)
g é a aceleração da gravidade (m/s²)
h é a altura em relação ao solo ou outro referencial (m)

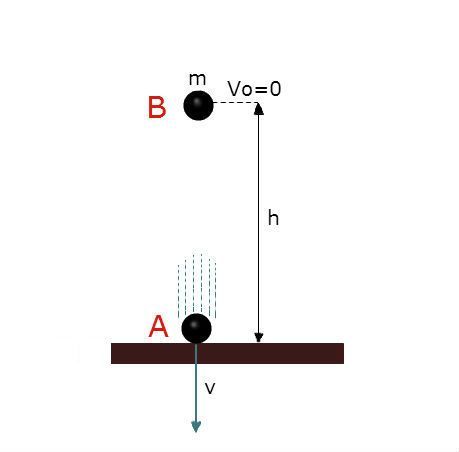O objeto de massa m se desloca a uma altura h, indo da posição B para A.

Assim, é necessário usar uma força para elevar um objeto até uma determinada altura, nesse ponto mais alto o objeto tem maior energia potencial. Quando o objeto desce libera sua energia, que será convertida em energia cinética.

Portanto, a energia potencial gravitacional do objeto está associada com a sua posição (altura relativa a um ponto de referência), com a sua massa e com a força da gravidade.

Considerando que a força exigida para elevar um objeto é igual ao seu peso, a energia potencial gravitacional é igual ao seu peso (m x g) multiplicado pela altura h a que foi elevado.

A força da gravidade varia com a altura, na superfície da Terra a diferença é muito pequena, assim considera-se a aceleração da gravidade como uma constante, de 9,8m/s², em qualquer parte.

Leia para saber mais sobre Energia Potencial Gravitacional.

Exemplo de energia potencial gravitacional
Um objeto de 2kg é lançado da janela de um prédio de 10 m. Considerando a aceleração da gravidade local g=10m/s². Qual é a Energia Potencial Gravitacional do objeto?

Resolução
A energia potencial gravitacional (Epg) está relacionada com o peso do objeto (massa x gravidade) e a altura do seu deslocamento. Então, calculamos a Epg usando os valores do enunciado.

$reto E com pg subscrito espaço igual a reto m espaço. espaço reto g espaço. espaço reto h espaço$

Com m = 2kg, g = 10m/s² e h = 10m.

$reto E com pg subscrito espaço igual a espaço 2 espaço.10.10 espaço espaço reto E com pg subscrito espaço igual a espaço 200 espaço reto J.$

Resposta
A Energia Potencial Gravitacional do objeto é igual a 200 Joules.

Energia Potencial Elástica

Um corpo elástico é aquele que sofre uma deformação, produzida por uma força externa, passando de uma posição A (não deformado) para uma posição B (deformado) e recupera sua forma e tamanho original, voltando a posição inicial.

Fórmula da energia potencial elástica

$começar estilo tamanho matemático 18px reto E com pe espaço subscrito fim do subscrito igual a numerador reto K. reto x ao quadrado sobre denominador 2 fim da fração fim do estilo$

Onde,
$começar estilo tamanho matemático 16px reto E com pe espaço subscrito fim do subscrito fim do estilo$ é a energia potencial elástica (J)
K é a constante elástica (N/m)
x é a deformação (m)

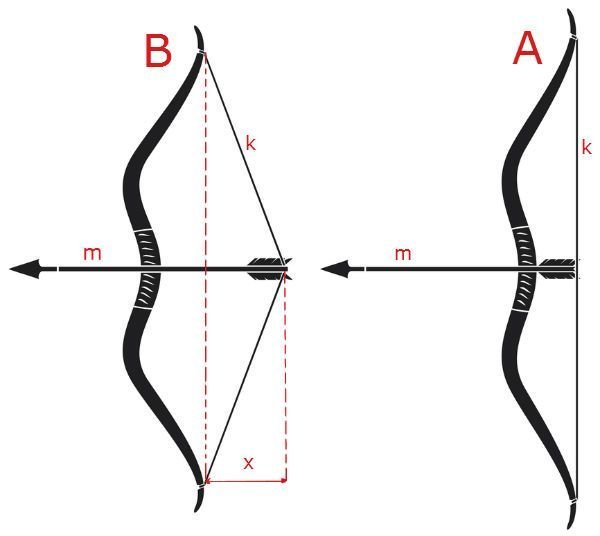Para lançar a flecha (corpo de massa m), o elástico do arco sofre uma deformação (medida por x) passando da posição de equilíbrio A para B.

Portanto, a posição de equilíbrio corresponde à posição onde o elástico ou a mola não está nem comprimida, nem esticada, é a sua posição natural.

A Energia Potencial Elástica está relacionada com o trabalho realizado pela força elástica do corpo para ir da posição deformada B para a posição inicial A.

Exemplo de energia potencial elástica
Uma mola de constante K =5000 N/m é comprimida por uma distância de 10 cm. Qual é a energia potencial elástica nela armazenada?

Resolução
A energia potencial elástica depende apenas da constante elástica da mola k e de sua deformação x. Então, calculamos a energia potencial usando os valores do enunciado.

$começar estilo tamanho matemático 16px reto E com pe espaço subscrito fim do subscrito igual a numerador reto K. reto x ao quadrado sobre denominador 2 fim da fração fim do estilo$

Com K=5000 N/m e x= 10cm ⇒ 0,1m

$reto E com pe subscrito espaço igual a espaço numerador 5000 espaço reto x espaço 0 vírgula 1 ao quadrado sobre denominador 2 fim da fração reto E com pe subscrito espaço igual a numerador espaço 5000 espaço reto x espaço 0 vírgula 01 sobre denominador 2 fim da fração reto E com pe subscrito espaço igual a 25 espaço reto J$

Resposta
A Energia Potencial armazenada na mola é igual a 25 joules.

Quer saber mais? Leia também os artigos:

Exercícios sobre energia potencial

Exercício 1

(Marinha 2021) Um guindaste do Arsenal de Marinha do Rio de Janeiro (AMRJ) suspende um objeto de 200Kg a uma altura de 5m acima do nível do mar. Desprezando as dimensões do objeto e adotando o valor da aceleração da gravidade local igual a 10 m/s², calcule a energia potencial do objeto em relação ao nível do mar, e marque a opção correta.

a) 2KJ
b) 4KJ
c) 6KJ
d) 8KJ
e) 10KJ

Ver Resposta

Resposta correta: e) 10KJ

Dados
m = 200Kg
h = 5m
g = 10m/s²

A energia potencial gravitacional é calculada pela fórmula:

$começar estilo tamanho matemático 16px reto E com pg espaço subscrito fim do subscrito igual a reto m. reto g. reto h fim do estilo$

Substituindo os valores:

$começar estilo tamanho matemático 16px reto E com pg espaço subscrito fim do subscrito igual a 200.10.5 espaço igual a espaço 10 espaço 000 reto J espaço igual a 10 KJ fim do estilo$

Exercício 2

(VUNESP 2017) Uma minicama elástica é constituída por uma superfície elástica presa a um aro lateral por 32 molas idênticas, como mostra a figura. Quando uma pessoa salta sobre esta minicama, transfere para ela uma quantidade de energia que é absorvida pela superfície elástica e pelas molas.

Considere que, ao saltar sobre uma dessas minicamas, uma pessoa transfira para ela uma quantidade de energia igual a 160 J, que 45% dessa energia seja distribuída igualmente entre as 32 molas e que cada uma delas se distenda 3,0 mm. Nessa situação, a constante elástica de cada mola, em N/m, vale

$a parêntese direito espaço 5 vírgula 0 espaço sinal de multiplicação espaço 10 à potência de 5 espaço.$

$b parêntese direito espaço 1 vírgula 6 espaço sinal de multiplicação espaço 10 à potência de 1 espaço.$

$c parêntese direito espaço 3 vírgula 2 espaço sinal de multiplicação espaço 10 ao cubo espaço.$

$d parêntese direito espaço 5 vírgula 0 espaço sinal de multiplicação espaço 10 ao cubo espaço.$

$e parêntese direito espaço 3 vírgula 2 espaço sinal de multiplicação espaço 10 à potência de 0 espaço.$

Ver Resposta

Resposta correta: $a parêntese direito espaço 5 vírgula 0 espaço sinal de multiplicação espaço 10 à potência de 5 espaço.$ .

Dados
32 molas
Energia absorvida 160J
Energia absorvida apenas pelas molas 45% de 160J
Distensão de cada mola de 3,0 mm = 0,003 m = $3 espaço x espaço 10 à potência de menos 3 fim do exponencial m$ .

Objetivo
Determinar K das molas.

Passo 1: energia absorvida por cada mola.

45% de 160J

$45 sobre 100 sinal de multiplicação 160 espaço igual a numerador espaço 7 espaço 200 sobre denominador 100 fim da fração igual a 72 J$

72J distribuídos para 32 molas significa que cada mola absorverá 2,25J.

$72 espaço dividido por espaço 32 espaço igual a espaço 2 vírgula 25 J$

Passo 2: determinar a constante K de cada mola.

A energia potencial elástica se relaciona com a constante elástica através da relação:

$reto E com pe espaço subscrito fim do subscrito igual a numerador reto K. reto x ao quadrado sobre denominador 2 fim da fração$

Isolando K, temos:

$numerador 2. E com p e subscrito fim do subscrito sobre denominador x ao quadrado fim da fração igual a K$

Substituindo os dados:

$numerador 2 espaço. espaço 2 vírgula 25 sobre denominador parêntese esquerdo 3 espaço. espaço 10 à potência de menos 3 fim do exponencial parêntese direito ao quadrado fim da fração igual a K numerador 4 vírgula 5 sobre denominador 9 espaço. espaço 10 à potência de menos 6 fim do exponencial fim da fração igual a K numerador 4 vírgula 5 sobre denominador 9 fim da fração. espaço 10 à potência de 6 igual a K 0 vírgula 5 espaço. espaço 10 à potência de 6 igual a K 5 vírgula 0 espaço. espaço 10 à potência de 5 igual a K$

Pratique mais com exercícios sobre energia potencial e cinética.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.