Associação de Resistores

Associação de Resistores é um circuito que apresenta dois ou mais resistores. Há três tipos de associação: em paralelo, em série e mista.

Ao analisar um circuito, podemos encontrar o valor do resistor equivalente, ou seja, o valor da resistência que sozinha poderia substituir todas as outras sem alterar os valores das demais grandezas associadas ao circuito.

Para calcular a tensão que os terminais de cada resistor está submetido aplicamos a Primeira Lei de Ohm:

U = R . i

Onde,

U: diferença de potencial elétrico (ddp), medida em Volts (V)
R: resistência, medida em Ohm (Ω)
i: intensidade da corrente elétrica, medida em Ampére (A).

Associação de Resistores em Série

Na associação de resistores em série, os resistores são ligados em sequência. Isso faz com que a corrente elétrica seja mantida ao longo do circuito, enquanto a tensão elétrica varia.

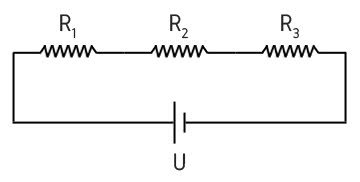
Assim, a resistência equivalente (R_eq) de um circuito corresponde à soma das resistências de cada resistor presente no circuito:

R_eq = R₁ + R₂ + R₃ +...+ R_n

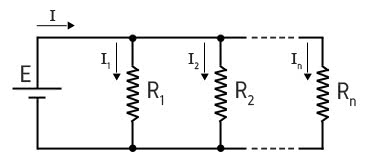
Associação de Resistores em Paralelo

Na associação de resistores em paralelo, todos os resistores estão submetidos a uma mesma diferença de potencial. Sendo a corrente elétrica dividida pelo ramos do circuito.

Assim, o inverso da resistência equivalente de um circuito é igual a soma dos inversos das resistências de cada resistor presente no circuito:

Quando, em um circuito em paralelo, o valor das resistências forem iguais, podemos encontrar o valor da resistência equivalente dividindo o valor de uma resistência pelo número de resistências do circuito, ou seja:

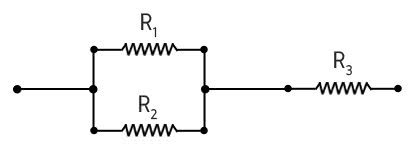
Associação de Resistores Mista

Na associação de resistores mista, os resistores são ligados em série e em paralelo. Para calculá-la, primeiro encontramos o valor correspondente à associação em paralelo e de seguida somamos aos resistores em série.

Leia

• Resistores
• Resistência Elétrica
• Fórmulas de Física
• Leis de Kirchhoff
• Associação de capacitares
• Eletrodinâmica
• Exercícios sobre Ponte de Wheatstone (com gabarito explicado)

Exercícios Resolvidos

1) UFRGS - 2018

Uma fonte de tensão cuja força eletromotriz é de 15 V tem resistência interna de 5 Ω. A fonte está ligada em série com uma lâmpada incandescente e com um resistor. Medidas são realizadas e constata-se que a corrente elétrica que atravessa o resistor é de 0,20 A, e que a diferença de potencial na lâmpada é de 4 V.

Nessa circunstância, as resistências elétricas da lâmpada e do resistor valem, respectivamente,

a) 0,8 Ω e 50 Ω.
b) 20 Ω e 50 Ω.
c) 0,8 Ω e 55 Ω.
d) 20 Ω e 55 Ω.
e) 20 Ω e 70 Ω.

2) PUC/RJ - 2018

Um circuito tem 3 resistores idênticos, dois deles colocados em paralelo entre si, e ligados em série com o terceiro resistor e com uma fonte de 12V. A corrente que passa pela fonte é de 5,0 mA.

Qual é a resistência de cada resistor, em kΩ?

a) 0,60
b) 0,80
c) 1,2
d) 1,6
e) 2,4

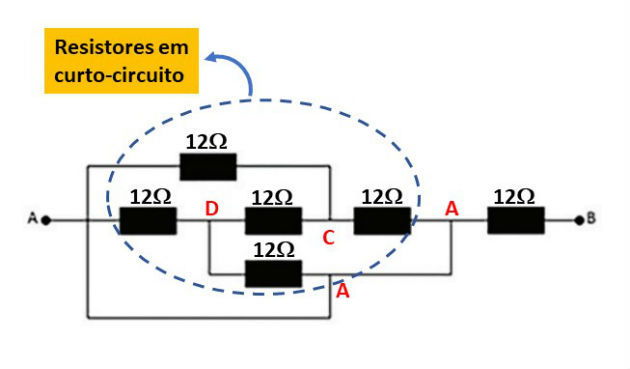
3) PUC/SP - 2018

Determine, em ohm, o valor da resistência do resistor equivalente da associação abaixo:

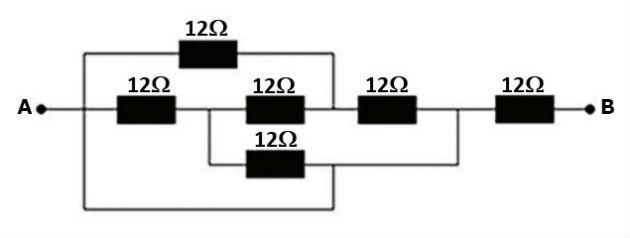
a) 0
b) 12
c) 24
d) 36