Força Elástica

Rafael C. Asth

Professor de Matemática e Física

A força elástica (F_el) é a força exercida sobre um corpo que possui elasticidade, por exemplo, uma mola, borracha ou elástico.

Essa força determina, portanto, a deformação desse corpo quando ele se estica ou se comprime. Isso dependerá da direção da força aplicada.

Como exemplo, pensemos numa mola presa num suporte. Se não houver uma força atuante sobre ela, dizemos que ela está em repouso. Por sua vez, quando esticamos essa mola, ela criará uma força em sentido contrário.

Note que a deformação sofrida pela mola é diretamente proporcional à intensidade da força aplicada. Sendo assim, quanto maior for a força aplicada (P), maior será a deformação da mola (x), como observamos na imagem abaixo:

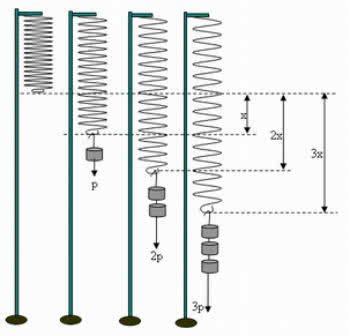
Fórmula da força elástica

Para calcular a força elástica, utilizamos uma fórmula elaborada pelo cientista inglês Robert Hooke (1635-1703), chamada de Lei de Hooke da força elástica.

Onde,

F: força aplicada no corpo elástico (N)
K: constante elástica (N/m)
x: variação sofrida pelo corpo elástico (m)

Constante Elástica

Vale lembrar que a chamada “constante elástica” é determinada pela natureza do material utilizado, e ainda, por suas dimensões.

Exemplo 1
Uma mola apresenta uma das extremidades fixadas a um suporte. Ao aplicar uma força na outra extremidade, essa mola sofre uma deformação de 5 m. Determine a intensidade da força aplicada, sabendo que a constante elástica da mola é de 110 N/m.

Para saber a intensidade da força exercida sobre a mola, devemos utilizar a fórmula da Lei de Hooke:

F = K . x
F = 110 . 5
F = 550 N

Exemplo 2
Determine a variação de uma mola que possui uma força atuante de 30N e sua constante elástica é de 300N/m.

Para encontrar a variação sofrida pela mola, utilizamos a fórmula da Lei de Hooke:

F = K . x
30 = 300 . x
x = 30/300
x = 0,1 m

Energia Potencial Elástica

A energia associada a força elástica é chamada de energia potencial elástica. Ela está relacionada com o trabalho realizado pela força elástica do corpo que vai da posição inicial até a posição deformada.

A fórmula para calcular a energia potencial elástica é expressa da seguinte forma:

Onde,

EP_e: energia potencial elástica
K: constante elástica
x: medida da deformação do corpo elástico

Quer saber mais? Leia também:

• Energia Potencial Elástica
• Força Centrípeta: o que é, fórmulas e exemplos
• Fórmulas de Física

Exercícios de Força Elástica com gabarito

Exercício 1

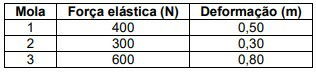
(Uern 2013) A tabela apresenta a força elástica e a deformação de 3 molas diferentes.
Comparando-se as constantes elásticas destas 3 molas, tem-se que

a) K1 > K2 > K3.
b) K2 > K1 > K3.
c) K2 > K3 > K1.
d) K3 > K2 > K1.

Exercício 2

(CAP 2015) Segundo a Lei de Hooke, é correto afirmar que:

a) um aumento na tensão provoca uma diminuição na deformação.
b) um aumento de tensão não provoca qualquer deformação.
c) a maioria dos materiais de engenharia apresenta relação não linear entre a tensão e a deformação na região de elasticidade do material.
d) um aumento na tensão provoca um aumento proporcional na deformação.
e) não existe nenhuma relação entre tensão e deformação.

Exercício 3

(EEAR 2019) Quatro molas ideais, A, B, C e D, com constantes elásticas respectivamente, kA = 20 N/m, kB = 40 N/m, kC = 2000 N/m e kD = 4000 N/m, estão presas, separadamente, ao teto de um laboratório por uma das suas extremidades. Dentre as quatro molas, determine aquela que ao ser colocado um corpo de massa igual a 40kg, na sua extremidade livre, sofre uma deformação de exatamente 20cm.

Considere o módulo da aceleração da gravidade no local igual a 10m/s² e que as molas obedecem à Lei de Hooke.

a) A
b) B
c) C
d) D

Veja também força de atrito.

Exercícios sobre força de tração

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.