Lançamento Oblíquo

Rafael C. Asth

Professor de Matemática e Física

O lançamento oblíquo ou de projétil é um movimento realizado por um objeto que é lançado na diagonal.

Esse tipo de movimento realiza uma trajetória parabólica, unindo movimentos na vertical (sobe e desce) e na horizontal. Assim, o objeto arremessado forma um ângulo (θ) entre 0° e 90° em relação a horizontal.

Na direção vertical ele realiza um Movimento Uniformemente Variado (MUV). Já na posição horizontal, o Movimento Retilíneo Uniforme (MRU).

Nesse caso, o objeto é lançado com uma velocidade inicial (v₀) e está sob a ação da força da gravidade (g).

Geralmente, a velocidade vertical é indicado por $V com y subscrito$ , enquanto a horizontal é $V com x subscrito$ . Isso porque quando ilustramos o lançamento oblíquo, utilizamos dois eixos (x e y) para indicar os dois movimentos realizados.

A posição inicial (s₀) indica o local onde tem início o lançamento. Já a posição final indica o local onde o objeto cessa o movimento parabólico.

Além disso, é importante notar que após lançado ele segue na direção vertical até atingir uma altura máxima e daí, tende a descer, também na vertical.

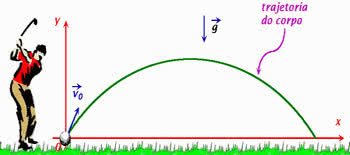
Como exemplos de lançamento oblíquo podemos citar: o chute de um futebolista, um atleta de salto à distância ou ainda, a trajetória realizada por uma bola de golfe.

Além do lançamento oblíquo, temos também:

Lançamento Vertical: objeto lançado que realiza um movimento na vertical.
Lançamento Horizontal: objeto lançado que realiza um movimento na horizontal.

Fórmulas para lançamento oblíquo

Como o lançamento oblíquo de um corpo produz um movimento parabólico, podemos analisar separadamente suas componentes: vertical e horizontal.

Para a direção vertical

Consideramos:

Movimento Uniformemente variado (MUV)
O início do movimento em seu ponto de lançamento, $S com 0 subscrito igual a 0$ .
A velocidade vertical final igual a zero, V = 0.
Sentido positivo para cima.
Desprezamos a resistência do ar.

Posição vertical em função do tempo (função horária da posição)

$começar estilo tamanho matemático 18px reto S com reto y subscrito parêntese esquerdo reto t parêntese direito igual a reto V com 0 com reto y subscrito subscrito fim do subscrito reto t espaço mais ou menos numerador espaço reto g sobre denominador 2 fim da fração reto t ao quadrado fim do estilo$

Onde,
$começar estilo tamanho matemático 16px reto S com reto y subscrito parêntese esquerdo reto t parêntese direito fim do estilo$ é a posição vertical em determinado instante após o lançamento.
$V com 0 com y subscrito subscrito fim do subscrito$ é a velocidade inicial na vertical.
g é a aceleração da gravidade.
t é o tempo.

O + ou - na fórmula depende da direção do movimento, negativo na subida, pois é a direção contrária a aceleração da gravidade.

Velocidade vertical em função do tempo (função horária da velocidade)

$começar estilo tamanho matemático 18px reto V com reto y subscrito parêntese esquerdo reto t parêntese direito igual a reto V com 0 com reto y subscrito subscrito fim do subscrito mais ou menos gt fim do estilo$

Dois valores são importantes no movimento vertical: a altura máxima o tempo até alcançar o ponto mais alto da trajetória.

Tempo de subida
Obtido pela função horária da velocidade isolando t e fazendo V(t) = 0.

$começar estilo tamanho matemático 18px reto t com reto s subscrito igual a reto V com 0 com reto y subscrito subscrito fim do subscrito sobre reto g fim do estilo$

Onde,

$t com s subscrito$ é o tempo de subida.
$V com 0 com y subscrito subscrito fim do subscrito$ é a velocidade vertical inicial.

O tempo de subida é igual ao tempo de descida, logo, o tempo total é duas o tempo de subida.

$começar estilo tamanho matemático 16px t com T subscrito espaço igual a espaço 2 t com s subscrito t com T subscrito espaço igual a 2 numerador espaço reto V com 0 com y subscrito subscrito fim do subscrito sobre denominador reto g fim da fração fim do estilo$

Assim vemos que o tempo de subida só depende da velocidade inicial, visto g ser constante.

Altura máxima
Obtida pela equação de Torricelli com V = 0 e S0 = 0.

$começar estilo tamanho matemático 18px reto h igual a numerador reto V com 0 com reto y subscrito subscrito fim do subscrito ao quadrado sobre denominador 2 reto g fim da fração fim do estilo$

Desta forma, a altura máxima só depende da velocidade inicial.

Para a direção horizontal

Consideramos:

Movimento Uniforme (MU)
Velocidade constante.
Sem aceleração.

A velocidade em qualquer ponto é igual à velocidade inicial.
$reto V parêntese esquerdo reto t parêntese direito espaço igual a espaço reto V com 0 subscrito com reto x subscrito$

Onde,
$Error converting from MathML to accessible text.$ é a velocidade horizontal inicial.

Posição horizontal em função do tempo

$começar estilo tamanho matemático 18px reto S com reto x subscrito parêntese esquerdo reto t parêntese direito igual a reto V com 0 com reto x subscrito subscrito fim do subscrito. espaço reto t fim do estilo$

Onde,
$começar estilo tamanho matemático 16px reto S com reto x subscrito parêntese esquerdo reto t parêntese direito fim do estilo$ é a posição horizontal em determinado instante t.

Movimento oblíquo em função do ângulo

O corpo lançado faz um ângulo $teta$ (teta) em relação à horizontal e com isto podemos decompor o vetor velocidade em uma componente horizontal Vx e uma componente vertical Vy.

Componente horizontal da velocidade

$V com 0 subscrito com x subscrito igual a V com 0 subscrito espaço. espaço cos espaço teta$

Componente vertical da velocidade

$V com 0 com y subscrito subscrito fim do subscrito igual a V com 0 subscrito espaço. espaço s e n espaço teta$

Substituindo estes valores nas fórmulas anteriores, obtemos:

Tempo de subida em função do ângulo

$reto t com reto s subscrito igual a numerador reto V com 0 subscrito espaço. espaço senθ sobre denominador reto g fim da fração$

Altura máxima em função do ângulo

$reto h igual a numerador reto v com 0 subscrito ao quadrado espaço. espaço sen ao quadrado reto teta sobre denominador 2 reto g fim da fração$

Onde,

h: altura máxima
v₀: velocidade inicial
sen θ: ângulo realizado pelo objeto
g: aceleração da gravidade

Alcance horizontal

$reto a igual a numerador reto V com 0 subscrito ao quadrado espaço. espaço sen espaço 2 reto teta sobre denominador reto g fim da fração$

Alcance e altura horizontal máximos

O alcance é máximo para um ângulo de 45°.

$reto a com máx subscrito igual a reto V com 0 subscrito ao quadrado sobre reto g$

Estas grandezas dependem do seno do ângulo de lançamento que, é uma função que varia entre 0 e, no máximo 1. Seno vale 1 quando o ângulo é de 90°.

Na fórmula do alcance, fazemos

$2 teta espaço igual a espaço 90 sinal de grau teta espaço igual a numerador 90 sinal de grau sobre denominador 2 fim da fração teta igual a 45 sinal de grau$

Para um ângulo de 45°, a altura máxima é:

$reto h igual a reto a com max subscrito sobre 4$

Veja também Velocidade relativa.

Exercícios de lançamento oblíquo

Exercício 1

(CEFET-CE) Duas pedras são lançadas do mesmo ponto no solo no mesmo sentido. A primeira tem velocidade inicial de módulo 20 m/s e forma um ângulo de 60° com a horizontal, enquanto, para a outra pedra, este ângulo é de 30°.

O módulo da velocidade inicial da segunda pedra, de modo que ambas tenham o mesmo alcance, é:

Despreze a resistência do ar.

a) 10 m/s
b) 10√3 m/s
c) 15 m/s
d) 20 m/s
e) 20√3 m/s

Ver Resposta

Resposta correta: d) 20 m/s.

O problema trata de um lançamento oblíquo.
Considerar $g espaço igual a espaço 10 espaço m dividido por s ao quadrado$

Dados
1ª pedra:
$V com 0 subscrito$ de 20 m/s (velocidade inicial)
$teta$ = 60° (ângulo de lançamento ou ângulo de tiro)

2ª pedra:
$V com 0 subscrito$ desconhecida. É o objetivo da questão.
$teta$ = 30° (ângulo de lançamento ou ângulo de tiro)

1º passo: calcular o alcance da primeira pedra.

$a igual a numerador V com 0 subscrito ao quadrado espaço. espaço s e n espaço 2 teta sobre denominador g fim da fração a igual a numerador 20 ao quadrado espaço. espaço s e n espaço 2.60 à potência de operador anelar sobre denominador 10 fim da fração a igual a numerador 400 espaço. espaço começar estilo mostrar numerador raiz quadrada de 3 sobre denominador 2 fim da fração fim do estilo sobre denominador 10 fim da fração a igual a 40. numerador raiz quadrada de 3 sobre denominador 2 fim da fração a igual a 20 raiz quadrada de 3 espaço m$

2º passo: calcular a velocidade inicial da segunda

Para isto, iremos utilizar o alcance da primeira.

$a igual a numerador V com 0 subscrito ao quadrado espaço. espaço s e n 2 teta sobre denominador g fim da fração 20 raiz quadrada de 3 igual a numerador V com 0 subscrito ao quadrado espaço. espaço s e n espaço 2.30 sobre denominador 10 fim da fração numerador 10 espaço. espaço 20 raiz quadrada de 3 sobre denominador s e n espaço 2.30 fim da fração igual a V com 0 subscrito ao quadrado numerador 200 raiz quadrada de 3 sobre denominador começar estilo mostrar numerador raiz quadrada de 3 sobre denominador 2 fim da fração fim do estilo fim da fração igual a V com 0 subscrito ao quadrado 200 raiz quadrada de 3 espaço. espaço numerador 2 sobre denominador raiz quadrada de 3 fim da fração igual a V com 0 subscrito ao quadrado 400 espaço igual a V com 0 subscrito ao quadrado raiz quadrada de 400 igual a V com 0 subscrito 20 igual a V com 0 subscrito$

Conclusão
A velocidade da segunda pedra deve ser de 20 m/s para que ela tenha o mesmo alcance da primeira.

Exercício 2

(PUCCAMP-SP) Observando a parábola do dardo arremessado por um atleta, um matemático resolveu obter uma expressão que lhe permitisse calcular a altura y, em metros, do dardo em relação ao solo, decorridos t segundos do instante de seu lançamento (t = 0).

Se o dardo chegou à altura máxima de 20 m e atingiu o solo 4 segundos após o seu lançamento, então, desprezada a altura do atleta, considerando g=10m/s², a expressão que o matemático encontrou foi

a) y = – 5t² + 20t
b) y = – 5t² + 10t
c) y = – 5t² + t
d) y = -10t² + 50
e) y = -10t² + 10

Ver Resposta

Resposta correta: a) y = – 5t² + 20t

Objetivo
Determinar a função horária da posição vertical.

Dados
Altura máxima de 20 m
Tempo total de 4s

Considerações
g=10m/s2
Desprezar resistência do ar.
Sentido positivo para cima.
Posição e tempo inicial iguais a zero no lançamento.

Resolução

1º passo: determinar a velocidade inicial.

Como o dardo está sujeito a ação da gravidade, na vertical, o movimento será uniformemente variado. A função horária é:

$y parêntese esquerdo t parêntese direito igual a y com 0 subscrito mais V com 0 subscrito. t espaço menos espaço 1 meio g. t ao quadrado$
Onde,
y(t) é a altura, a posição em y no instante t.
y0 é a posição inicial.
V0 é a velocidade inicial.

O sinal negativo se deve ao fato da gravidade e o movimento vertical possuírem sentidos opostos.

O tempo total é igual a duas vezes o tempo de subida, assim, levaram-se 2s até o ponto máximo do movimento, instante em que a altura foi de 20 m.

Substituindo na equação determinamos a velocidade inicial.

$20 espaço igual a espaço 0 espaço mais espaço V com 0 subscrito.2 espaço menos espaço 10 sobre 2. espaço 2 ao quadrado 20 espaço igual a espaço 2 V com 0 subscrito espaço menos espaço 5.4 20 espaço igual a espaço 2 V com 0 subscrito espaço menos espaço 20 40 espaço igual a 2 V com 0 subscrito 40 sobre 2 igual a V com 0 subscrito 20 igual a V com 0 subscrito$

Assim, a velocidade inicial do dardo foi de 20 m/s.

2º passo: escrever a função horária da altura.

Utilizamos a função horária com:
V0 = 20
y0 = 0

Conclusão

$y parêntese esquerdo t parêntese direito igual a menos 5 t ao quadrado mais espaço 20 t$

Exercício 3

(UFSM-RS) Um índio dispara uma flecha obliquamente. Sendo a resistência do ar desprezível, a flecha descreve uma parábola num referencial fixo ao solo. Considerando o movimento da flecha depois que ela abandona o arco, afirma-se:

I. A flecha tem aceleração mínima, em módulo, no ponto mais alto da trajetória.
II. A flecha tem aceleração sempre na mesma direção e no mesmo sentido.
III. A flecha atinge a velocidade máxima, em módulo, no ponto mais alto da trajetória.

Está (ão) correta(s)

a) apenas I
b) apenas I e II
c) apenas II
d) apenas III
e) I, II e III

Ver Resposta

Resposta correta: c) apenas II

I) ERRADA: A flecha está sujeita a aceleração da gravidade em todo o trajeto.

III) ERRADA: No ponto mais alto da trajetória a velocidade vertical é nula.

Veja também força elástica.

Pratique exercícios sobre queda livre.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.