Cinemática
Na área de Mecânica da Física, a Cinemática estuda e descreve o movimento dos corpos sem se preocupar com as causas do deslocamento.
Através da Cinemática é possível classificar e comparar os movimentos, já o motivo da ocorrência é abordado na Dinâmica.
Conceitos fundamentais
Veja a seguir alguns conceitos importantes no estudo da Cinemática.
- Referencial: ponto que determina se o objeto está em movimento ou repouso.
- Movimento: mudança de posição para se aproximar ou afastar do referencial.
- Repouso: quando a posição de um objeto não se altera em relação a um referencial.
- Trajetória: linha que determina as diversas posições do objeto ao decorrer do tempo.
- Deslocamento: distância percorrida entre o espaço inicial e final da trajetória.
- Ponto material: corpo cujas dimensões não interferem no estudo do movimento.
- Corpo extenso: corpo cujas dimensões são importantes para o entender o movimento.
Exemplo: Um rapaz dentro de um carro é tido como A e se movimenta para direita em direção ao referencial B, que corresponde a uma menina parada próximo à faixa de pedestres.

Sendo B o referencial, dizemos que A está em movimento em relação a B, ou seja, está realizando uma trajetória, pois a distância que ele está de B varia com o tempo. Note que o movimento realizado por um corpo depende do referencial adotado.
O tipo de trajetória classifica o movimento em retilíneo, quando o movimento é realizado em uma reta, ou curvilíneo, quando o movimento é realizado em uma trajetória curva.
Fórmulas da Cinemática
Velocidade escalar média
A rapidez com que é realizado o deslocamento por um corpo recebe o nome de velocidade média, que pode ser calculada através da seguinte fórmula:
Os termos inicial e final correspondem ao período de contagem do tempo, não importando se o carro ficou parado durante algum momento ou se houve variação de velocidade no percurso.
No Sistema Internacional (SI) a unidade de velocidade média é o metro por segundo (m/s).
Veja também: Fórmulas de Cinemática
Aceleração escalar média
Com o passar do tempo, a velocidade de um corpo pode mudar à medida que ele realiza o movimento. A aceleração de um corpo faz com que a variação da velocidade durante um trajeto aumente ou diminua em um dado intervalo de tempo.
Veja a seguir a fórmula para calcular a aceleração:
No Sistema Internacional (SI) a unidade de aceleração média é o metro por segundo ao quadrado (m/s2).
Veja também: Aceleração
Movimento Uniforme (MU)
Se em igual intervalo de tempo um corpo percorre sempre a mesma distância, seu movimento é classificado como uniforme. Sendo assim, sua velocidade é constante e diferente de zero ao longo do percurso.
No Movimento Retilíneo Uniforme (MRU) a velocidade não muda em uma trajetória realizada em linha reta.
A posição do corpo na trajetória pode ser calculada pela função horária da posição:
Onde,
S = posição final, em metros (m)
S0 = posição inicial, em metros (m)
v = velocidade, em metros por segundo (m/s)
t = tempo, em segundos (s)
Veja também: Movimento Uniforme
Movimento Uniformemente Variado (MUV)
Se a velocidade variar em quantidades iguais no mesmo intervalo de tempo, o movimento é caracterizado como uniformemente variado. Sendo assim, a aceleração é constante e diferente de zero.
O Movimento Retilíneo Uniformemente Variado (MRUV) é caracterizado pela mesma quantidade de aceleração de um corpo em linha reta.
Através da equação horária da velocidade é possível calcular a velocidade em função do tempo.
Onde,
V = velocidade final, em metros por segundo (m/s)
V0 = velocidade inicial, em metros por segundo (m/s)
a = aceleração, em metros por segundo ao quadrado (m/s2)
t = tempo, em segundos (s)
A posição do corpo durante a trajetória pode ser calculada através da seguinte equação:
Onde,
S = posição final, em metros (m)
S0 = posição inicial, em metros (m)
V0 = velocidade inicial, em metros por segundo (m/s)
a = aceleração, em metros por segundo ao quadrado (m/s2)
t = tempo, em segundos (s)
A equação de Torricelli é utilizada para relacionar a velocidade e o espaço percorrido no movimento uniformemente variado.
Onde,
V = velocidade final, em metros por segundo (m/s)
V0 = velocidade inicial, em metros por segundo (m/s)
a = aceleração, em metros por segundo ao quadrado (m/s2)
= espaço percorrido, em metros (m)
Veja também: Movimento Uniformemente Variado
Exercícios
Exercício 1
(FUVEST 2020) Um drone voando na horizontal, em relação ao solo (como indicado pelo sentido da seta na figura), deixa cair um pacote de livros. A melhor descrição da trajetória realizada pelo pacote de livros, segundo um observador em repouso no solo, é dada pelo percurso descrito na
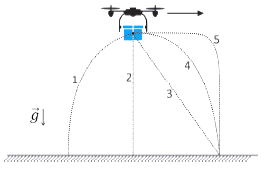
a) trajetória 1.
b) trajetória 2.
c) trajetória 3.
d) trajetória 4.
e) trajetória 5.
Exercício 2
(Enem 2013) Conta-se que um curioso incidente aconteceu durante a Primeira Guerra Mundial. Quando voava a uma altitude de dois mil metros, um piloto francês viu o que acreditava ser uma mosca parada perto de sua face. Apanhando-a rapidamente, ficou surpreso ao verificar que se tratava de um projétil alemão.
PERELMAN, J. Aprenda física brincando. São Paulo: Hemus, 1970.
O piloto consegue apanhar o projétil, pois
a) ele foi disparado em direção ao avião francês, freado pelo ar e parou justamente na frente do piloto.
b) o avião se movia no mesmo sentido que o dele, com velocidade visivelmente superior.
c) ele foi disparado para cima com velocidade constante, no instante em que o avião francês passou.
d) o avião se movia no sentido oposto ao dele, com velocidade de mesmo valor.
e) o avião se movia no mesmo sentido que o dele, com velocidade de mesmo valor.
Exercício 3
(UEG 2019) Em um dia de tempestade, você ouve um trovão 10 segundos após ver o clarão do relâmpago. Com o conhecimento de que a velocidade do som seja aproximada para 340 m/s, a distância que você se encontra da tempestade é, aproximadamente, de
a) 34 m
b) 34 km
c) 3,4 m
d) 3,4 km
e) 340 m
Utilize as listas de exercícios a seguir para praticar a utilização das fórmulas e adquirir mais conhecimento.
- Exercícios de Cinemática
- Exercícios de Velocidade Média
- Exercícios sobre Movimento Uniforme
- Exercícios sobre Movimento Uniformemente Variado.
- Equação de Torricelli
- Velocidade relativa
- Lançamento Oblíquo
- Movimento Progressivo e Movimento Retrógrado
ASTH, Rafael. Cinemática. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/cinematica/. Acesso em:


