Exercícios sobre Movimento Uniforme (com respostas comentadas)

Rafael C. Asth

Professor de Matemática e Física

O movimento uniforme é aquele cuja a velocidade não sofre variações ao longo do tempo. Quando o movimento segue uma trajetória em linha reta, é chamado de movimento retilíneo uniforme (MRU).

Aproveite as questões resolvidas e comentadas abaixo para verificar seus conhecimentos sobre esse importante assunto da cinemática.

Questão 1

Em relação ao movimento uniforme (MU), avalie as seguintes afirmações como verdadeiras (V) ou falsas (F):

1. ( ) No movimento uniforme, a velocidade do objeto muda ao longo do tempo.
2. ( ) A aceleração no movimento uniforme é sempre nula.
3. ( ) A distância percorrida em intervalos de tempo iguais é sempre a mesma no movimento uniforme.
4. ( ) No movimento uniforme, a velocidade média é igual à velocidade instantânea em qualquer momento.

Questão 2

Um carro percorre uma estrada retilínea com velocidade constante de 20 m/s. Determine a distância percorrida pelo carro em 40 segundos.

a) 400 m
b) 800 m
c) 600 m
d) 1000 m
e) 1200 m

Questão 3

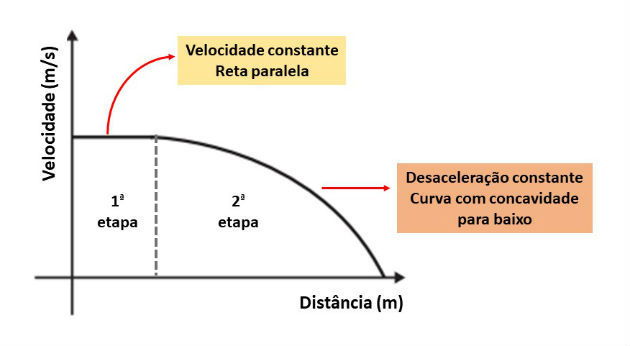
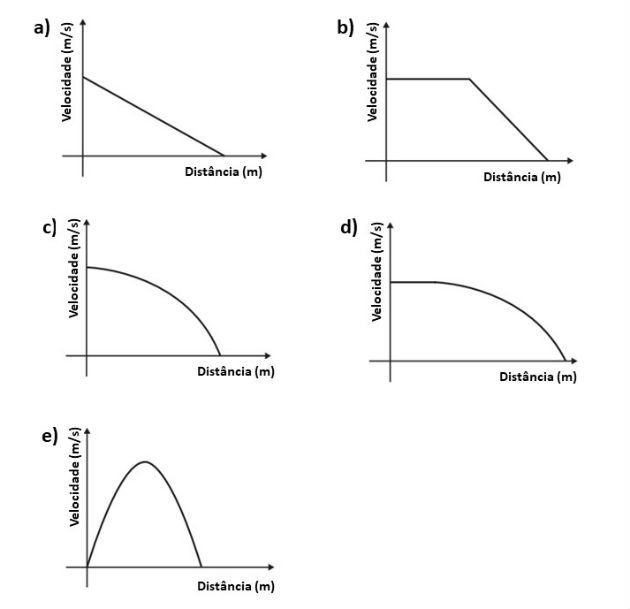
(Enem - 2016) Dois veículos que trafegam com velocidade constante em uma estrada, na mesma direção e sentido, devem manter entre si uma distância mínima. Isso porque o movimento de um veículo, até que ele pare totalmente, ocorre em duas etapas, a partir do momento em que o motorista detecta um problema que exige uma freada brusca. A primeira etapa é associada à distância que o veículo percorre entre o intervalo de tempo da detecção do problema e o acionamento dos freios. Já a segunda se relaciona com a distância que o automóvel percorre enquanto os freios agem com desaceleração constante.

Considerando a situação descrita, qual esboço gráfico representa a velocidade do automóvel em relação à distância percorrida até parar totalmente?

Questão 4

(Cefet - MG - 2018) Dois amigos, Pedro e Francisco, planejam fazer um passeio de bicicleta e combinam encontrarem-se no meio do caminho. Pedro fica parado no local marcado, aguardando a chegada do amigo. Francisco passa pelo ponto de encontro com uma velocidade constante de 9,0 m/s. No mesmo instante, Pedro começa a se mover com uma aceleração também constante de 0,30 m/s². A distância percorrida por Pedro até alcançar Francisco, em metros, é igual a

a) 30
b) 60
c) 270
d) 540

Veja também: Fórmulas de Cinemática

Questão 5

(UFRGS - 2018) Em grandes aeroportos e shoppings, existem esteiras móveis horizontais para facilitar o deslocamento de pessoas. Considere uma esteira com 48 m de comprimento e velocidade de 1,0 m/s. Uma pessoa ingressa na esteira e segue caminhando sobre ela com velocidade constante no mesmo sentido de movimento da esteira. A pessoa atinge a outra extremidade 30 s após ter ingressado na esteira. Com que velocidade, em m/s, a pessoa caminha sobre a esteira?

a) 2,6
b) 1,6
c) 1,0
d) 0,8
e) 0,6

Veja também: Exercícios sobre velocidade média

Questão 6

(UNESP - 2018) Juliana pratica corridas e consegue correr 5,0 km em meia hora. Seu próximo desafio é participar da corrida de São Silvestre, cujo percurso é de 15 km. Como é uma distância maior do que a que está acostumada a correr, seu instrutor orientou que diminuísse sua velocidade média habitual em 40% durante a nova prova. Se seguir a orientação de seu instrutor, Juliana completará a corrida de São Silvestre em

a) 2 h 40 min
b) 3 h 00 min
c) 2 h 15 min
d) 2 h 30 min
e) 1 h 52 min

Questão 7

(Unicamp - 2018) Situado na costa peruana, Chankillo, o mais antigo observatório das Américas, é composto por treze torres que se alinham de norte a sul ao longo de uma colina. Em 21 de dezembro, quando ocorre o solstício de verão no Hemisfério Sul, o Sol nasce à direita da primeira torre (sul), na extrema direita, a partir de um ponto de observação definido. À medida que os dias passam, a posição em que o Sol nasce se desloca entre as torres rumo à esquerda (norte). Pode-se calcular o dia do ano, observando-se qual torre coincide com a posição do Sol ao amanhecer. Em 21 de junho, solstício de inverno no Hemisfério Sul, o Sol nasce à esquerda da última torre na extrema esquerda e, à medida que os dias passam, vai se movendo rumo à direita, para reiniciar o ciclo no dezembro seguinte. Sabendo que as torres de Chankillo se posicionam ao longo de 300 metros no eixo norte-sul, a velocidade escalar média com a qual a posição do nascer do Sol se desloca através das torres é de aproximadamente

a) 0,8 m/dia.
b) 1,6 m/dia.
c) 25 m/dia.
d) 50 m/dia.

Questão 8

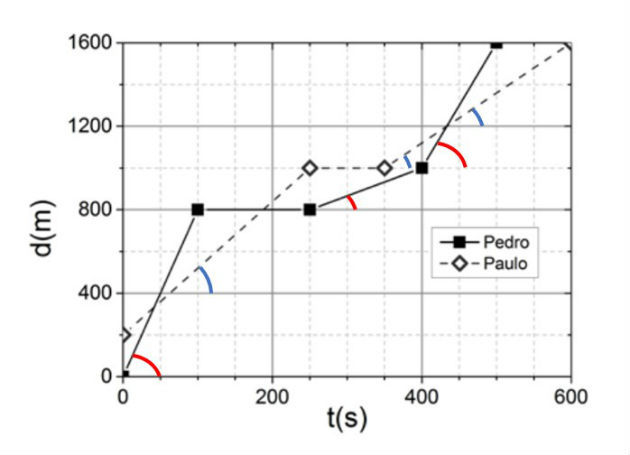
(UFRGS - 2016) Pedro e Paulo diariamente usam bicicletas para ir ao colégio. O gráfico abaixo mostra como ambos percorreram as distâncias até o colégio, em função do tempo, em certo dia.

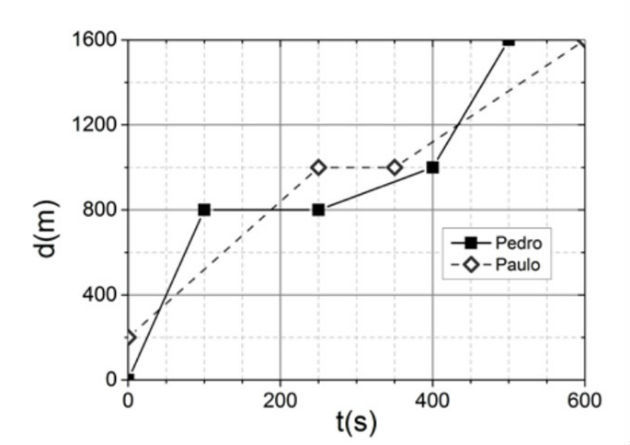
Com base no gráfico, considere as seguintes afirmações.

I - A velocidade média desenvolvida por Pedro foi maior do que a desenvolvida por Paulo.
II - A máxima velocidade foi desenvolvida por Paulo.
III- Ambos estiveram parados pelo mesmo intervalo de tempo, durante seus percursos.

Quais estão corretas?

a) Apenas I.
b) Apenas II.
c) Apenas III.
d) Apenas II e III.
e) I, II e III.

Questão 9

(UERJ - 2010) Um foguete persegue um avião, ambos com velocidades constantes e mesma direção. Enquanto o foguete percorre 4,0 km, o avião percorre apenas 1,0 km. Admita que, em um instante t₁, a distância entre eles é de 4,0 km e que, no instante t₂ , o foguete alcança o avião.
No intervalo de tempo t₂ - t₁, a distância percorrida pelo foguete, em quilômetros, corresponde aproximadamente a:

a) 4,7
b) 5,3
c) 6,2
d) 8,6

Veja também: Movimento Uniformemente Variado - Exercícios

Questão 10

(Enem - 2012) Uma empresa de transportes precisa efetuar a entrega de uma encomenda o mais breve possível. Para tanto, a equipe de logística analisa o trajeto desde a empresa até o local da entrega. Ela verifica que o trajeto apresenta dois trechos de distâncias diferentes e velocidades máximas permitidas diferentes. No primeiro trecho, a velocidade máxima permitida é de 80 km/h e a distância a ser percorrida é de 80 km. No segundo trecho, cujo comprimento vale 60 km, a velocidade máxima permitida é 120 km/h. Supondo que as condições de trânsito sejam favoráveis para que o veículo da empresa ande continuamente na velocidade máxima permitida, qual será o tempo necessário, em horas, para a realização da entrega?

a) 0,7
b) 1,4
c) 1,5
d) 2,0
e) 3,0

Veja também: Cinemática

Questão 11

(FATEC - 2018) Os dispositivos eletrônicos colocados em vias públicas, conhecidos como Radares Fixos (ou “pardais”), funcionam por meio de um conjunto de sensores dispostos no chão dessas vias. Os laços detectores (conjunto de dois sensores eletromagnéticos) são colocados em cada faixa de rolamento. Uma vez que motocicletas e automóveis possuem materiais ferromagnéticos, ao passarem pelos sensores, os sinais afetados são processados e determinadas duas velocidades. Uma entre o primeiro e o segundo sensor (1º laço); e a outra entre o segundo e o terceiro sensor (2º laço), conforme a figura.

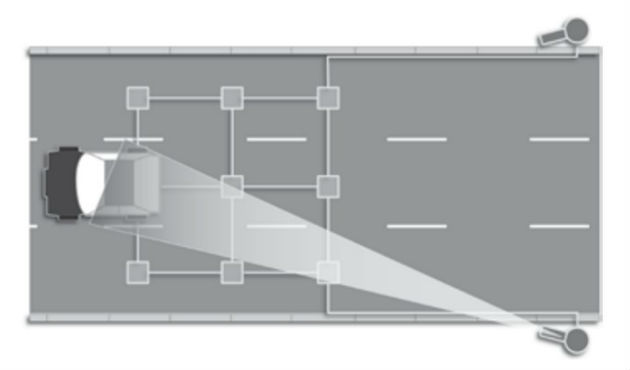
Essas duas velocidades medidas são validadas e correlacionadas com as velocidades a serem consideradas (V_C), conforme apresentado na tabela parcial de valores referenciais de velocidade para infrações (art. 218 do Código de Trânsito Brasileiro – CTB). Caso essas velocidades verificadas no 1º e no 2º laço sejam iguais, esse valor é denominado velocidade medida (V_M), e ele é relacionado à velocidade considerada (V_C). A câmera fotográfica é acionada para registrar a imagem da placa do veículo a ser multado apenas nas situações em que esse esteja trafegando acima do limite máximo permitido para aquele local e faixa de rolamento, considerando os valores de V_C.

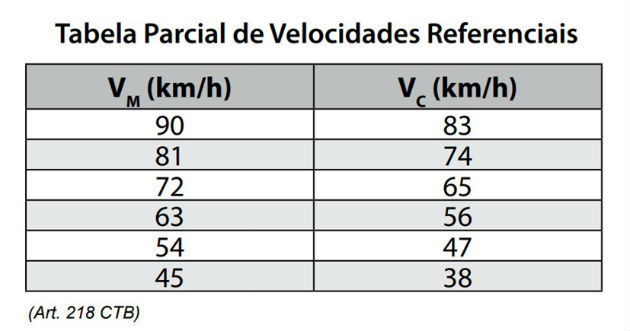
Considere que, em cada faixa de rolagem, os sensores estejam distantes entre si cerca de 3 metros e suponha que o carro da figura esteja deslocando-se para a esquerda e passe pelo primeiro laço com uma velocidade de 15 m/s, levando, portanto, 0,20 s para passar pelo segundo laço. Se a velocidade limite dessa pista for 50 km/h, podemos afirmar que o veículo

a) não será multado, pois V_M é menor do que a velocidade mínima permitida.
b) não será multado, pois V_C é menor do que a velocidade máxima permitida.
c) não será multado, pois V_C é menor do que a velocidade mínima permitida.
d) será multado, pois V_M é maior do que a velocidade máxima permitida.
e) será multado, pois V_C é maior do que a velocidade máxima permitida.

Para saber mais, veja também:

• Movimento Uniforme
• Movimento Retilíneo Uniforme
• Movimento Uniformemente Variado
• Movimento Retilíneo Uniformemente Variado
• Velocidade relativa
• Movimento Progressivo e Movimento Retrógrado

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.