ASSINAR TODA MATÉRIA+

Escalas Termométricas - Exercícios

Rafael C. Asth
Rafael C. Asth
Professor de Matemática e Física

As escalas termométricas são usadas para definir os valores de temperatura obtidos por um determinado instrumento de medida.

As principais escalas utilizadas são Celsius, Kelvin e Fahrenheit. Os valores em uma escala podem ser transformados em uma outra escala usando fórmulas de conversão.

Aproveite os exercícios comentados e resolvidos para tirar as suas dúvidas sobre esse assunto.

Questão 1

Transformando a temperatura de 25 ºC para a escala Fahrenheit e, em seguida, convertendo-a para escala Kelvin, quais as temperaturas registradas nas respectivas escalas?

a) 25 ºC; 50 ºF e 150 K.
b) 25 ºC; 88 ºF e 136 K.
c) 25 ºC; 77 ºF e 298 K.
d) 25 ºC; 36 ºF e 194 K.

Resposta correta: c) 25 ºC; 77 ºF e 298 K.

De acordo com a questão precisamos converter as escalas termométricas da seguinte forma:

tabela linha com Celsius seta para a direita Farenheit seta para a direita Kelvin linha com célula com 25 espaço º reto C fim da célula blank célula com reto X espaço º reto F fim da célula blank célula com reto Y espaço reto K fim da célula fim da tabela

Para isso, podemos utilizar a seguinte relação:

numerador º reto C sobre denominador 5 fim da fração espaço igual a espaço numerador º reto F espaço menos espaço 32 sobre denominador 9 fim da fração espaço igual a espaço numerador reto K espaço menos espaço 273 sobre denominador 5 fim da fração

1º Passo: conversão da escala Celsius para Fahrenheit.

numerador º reto C sobre denominador 5 fim da fração espaço igual a espaço numerador º reto F espaço menos espaço 32 sobre denominador 9 fim da fração 25 sobre 5 espaço igual a espaço numerador reto X espaço menos espaço 32 sobre denominador 9 fim da fração espaço 5 espaço igual a espaço numerador reto X espaço menos espaço 32 sobre denominador 9 fim da fração espaço 5 espaço. espaço 9 espaço igual a espaço reto X espaço menos espaço 32 45 espaço igual a espaço reto X espaço menos espaço 32 45 espaço mais espaço 32 espaço igual a espaço reto X reto X espaço igual a espaço 77 espaço º reto F

2º Passo: conversão da escala Fahrenheit para Kelvin.

numerador º reto F espaço menos espaço 32 sobre denominador 9 fim da fração espaço igual a espaço numerador reto K espaço menos espaço 273 sobre denominador 5 fim da fração numerador 77 espaço menos espaço 32 sobre denominador 9 fim da fração espaço igual a espaço numerador reto Y espaço menos espaço 273 sobre denominador 5 fim da fração 45 sobre 9 espaço igual a espaço numerador reto Y espaço menos espaço 273 sobre denominador 5 fim da fração 5 espaço igual a espaço numerador reto Y espaço menos espaço 273 sobre denominador 5 fim da fração 5 espaço. espaço 5 espaço igual a espaço reto Y espaço menos espaço 273 25 espaço igual a espaço reto Y espaço menos espaço 273 25 espaço mais espaço 273 espaço igual a espaço reto Y reto Y espaço igual a espaço 298 espaço reto K

Portanto, a resposta correta é 25 ºC; 77 ºF e 298 K.

Questão 2

Dois termômetros, um com a escala Celsius e outro na escala Kelvin, foram colocados no mesmo fluido. Sabendo que a temperatura registrada na escala Celsius era de 40 ºC, qual a temperatura marcada no termômetro em Kelvin?

a) 298 K
b) 254 K
c) 348 K
d) 313 K

Resposta correta: d) 313 K.

Para resolver esta questão, precisamos relacionar as temperaturas Celsius e Kelvin. Portanto, utilizaremos a seguinte equação:

reto T com reto K subscrito espaço igual a espaço reto T com º reto C subscrito fim do subscrito espaço mais espaço 273

Agora, só precisamos substituir a temperatura de 40 ºC na equação e calcular em Kelvin.

reto T espaço igual a espaço 40 espaço mais espaço 273 espaço espaço reto T espaço igual a espaço 313 espaço reto K

Portanto, quando um termômetro marca 40 ºC o outro indica a temperatura 313 K.

Questão 3

Em um experimento no laboratório, um aluno decidiu observar a variação de temperatura em relação ao comprimento da coluna de mercúrio no interior de dois termômetros.

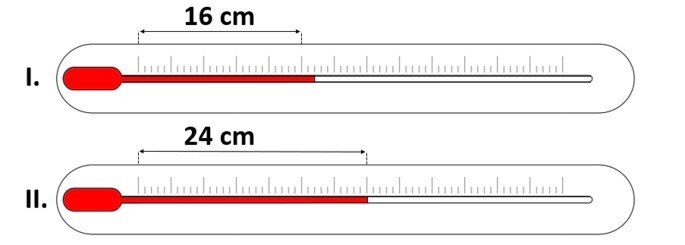
Conversão de escalas termométricas

Sabendo que o mercúrio é sensível ao calor e a temperatura marcada no termômetro é proporcional ao deslocamento do fluido no tubo, qual a temperatura no termômetro I, em graus Celsius, sabendo que o termômetro II marca 48 ºC?

a) 16 ºC
b) 32 ºC
c) 28 ºC
d) 46 ºC

Resposta correta: b) 32 ºC.

Quando duas grandezas são proporcionais, então a razão entre as duas variáveis produz uma constante de proporcionalidade.

Neste caso, a temperatura (T) é proporcional ao comprimento da coluna de mercúrio (C).

reto T sobre reto C espaço igual a espaço reto K

Portanto, para descobrirmos a temperatura, podemos multiplicar o comprimento pela constante K, ou seja:

reto T com 1 subscrito espaço igual a espaço reto K espaço. espaço 16 espaço reto T com 2 subscrito espaço igual a espaço reto K. espaço 24

Como vimos, T/C = K e a temperatura no termômetro II é de 48 ºC. Então:

numerador reto T com 2 subscrito sobre denominador reto C com 2 subscrito espaço fim da fração igual a espaço reto K espaço 48 sobre 24 espaço igual a espaço 2

Agora que descobrimos o valor da constante de proporcionalidade podemos calcular a temperatura no termômetro I.

reto T com 1 subscrito espaço igual a espaço reto K espaço. espaço reto C com 1 subscrito espaço reto T com 1 subscrito espaço igual a espaço 2 espaço. espaço 16 espaço igual a espaço 32 espaço º reto C

Portanto, a temperatura no termômetro I é de 32 ºC.

Questão 4

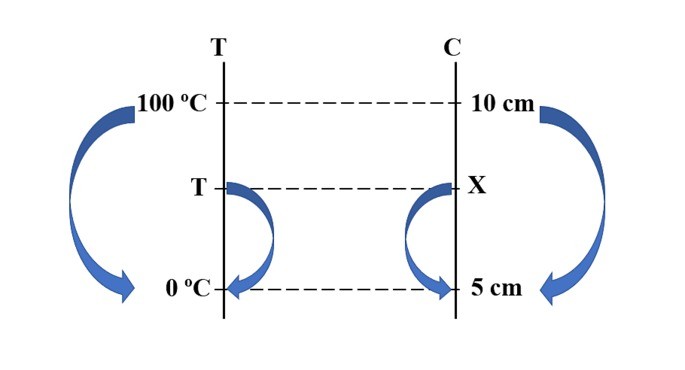
Para calibrar um termômetro, um técnico relacionou a temperatura medida e o comprimento da coluna de mercúrio no interior do termômetro e os dados obtidos foram:

1. Quando a temperatura registrada era de 0 ºC, o fluido apresentava um deslocamento de 5 cm.
2. Ao atingir a temperatura de 100 ºC, o comprimento registrado foi de 10 cm.

A partir dessas informações, determine, por uma função termométrica, a relação existente entre a temperatura e o comprimento da coluna de mercúrio.

a) T = 20X - 100
b) T = 5X - 100
c) T = x - 100
d) T = 15x - 100

Resposta correta: a) T = 20X - 100.

Nesta questão podemos observar a proporcionalidade entre a temperatura e o comprimento da coluna de mercúrio.

Para determinar uma temperatura arbitrária (T), vamos relacioná-la com um determinado comprimento (X) e com os dados da questão da seguinte forma:

Questão sobre escalas termométricas

Portanto,

numerador reto T espaço menos espaço 0 sobre denominador 100 espaço menos espaço 0 fim da fração igual a espaço numerador reto X espaço menos espaço 5 sobre denominador 10 espaço menos espaço 5 fim da fração espaço reto T sobre 100 espaço igual a espaço numerador reto X espaço menos espaço 5 sobre denominador 5 fim da fração espaço reto T espaço igual a espaço numerador 100 espaço reto X espaço menos espaço 500 sobre denominador 5 fim da fração reto T espaço igual a espaço 20 reto X espaço menos espaço 100

Vamos aplicar a temperatura de 25 ºC para testar essa função.

reto T espaço igual a espaço 20. reto X espaço menos espaço 100 25 espaço igual a espaço 20. reto X espaço menos espaço 100 25 espaço mais espaço 100 espaço igual a espaço 20. reto X 125 sobre 20 igual a espaço reto X reto X espaço igual a espaço 6 vírgula 25

No exemplo acima, aplicando a função termométrica, descobrimos que quando a temperatura é de 25 ºC a coluna de mercúrio tem um comprimento de 6,25 cm.

Questão 5

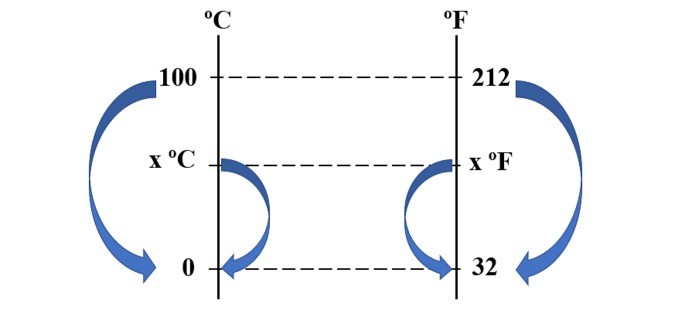
Comparando as medidas de temperatura nas escalas Celsius e Fahrenheit observa-se que enquanto na primeira escala a temperatura de ebulição da água é de 100 ºC, na segunda escala a água passa para o estado gasoso em 212 ºF. Já a fusão da água ocorre em 0 ºC e a respectiva temperatura na outra escala é 32 ºF.

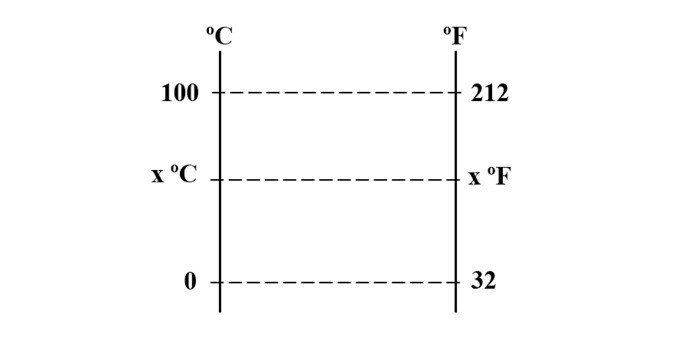
Escalas termométricas Celsius e Fahrenheit

Observe o gráfico e assinale a alternativa com a temperatura que pode ser marcada pelo mesmo número nas duas escalas.

a) 30
b) 10
c) - 20
d) - 40

Resposta correta: d) - 40.

Como o gráfico nos dá as temperaturas equivalentes nas duas escalas, podemos calcular a temperatura através da variação observada.

Escalas Celsius e Fahrenheit

numerador reto X espaço º reto C espaço menos espaço 0 sobre denominador 100 espaço menos espaço 0 fim da fração igual a espaço numerador reto X espaço º reto F espaço menos espaço 32 sobre denominador 212 espaço menos espaço 32 fim da fração reto X sobre 100 espaço igual a espaço numerador reto X espaço menos espaço 32 sobre denominador 180 fim da fração 180 reto X espaço igual a espaço 100 reto X espaço menos espaço 3200 espaço espaço 180 reto X espaço menos espaço 100 reto X espaço igual a espaço menos espaço 3200 espaço espaço 80 reto X espaço igual a espaço menos espaço 3200 espaço espaço reto X espaço igual a espaço numerador menos espaço 3200 sobre denominador espaço em branco fim da fração reto X espaço igual a espaço menos espaço 40

Portanto, quando na escala Celsius estiver indicando – 40, o mesmo valor será dado na escala Fahrenheit.

Veja também: Escalas Termométricas

Questão 6

(EsPECx - 2013) Um termômetro digital, localizado em uma praça na Inglaterra, marca a temperatura de 10,4 ºF. Essa temperatura, na escala Celsius, corresponde a

a) - 5 ºC
b) - 10 ºC
c) - 12 ºC
d) - 27 ºC
e) - 39 ºC

Resposta correta: c) - 12 ºC.

Para transformar da escala Fahrenheit para a escala Celsius, usaremos a seguinte relação:

numerador reto T com reto c subscrito sobre denominador 5 espaço fim da fração igual a numerador reto T com reto F subscrito menos 32 sobre denominador 9 fim da fração

Substituindo TF pelo valor da temperatura do termômetro, temos:

reto T com reto c subscrito sobre 5 igual a numerador 10 vírgula 4 menos 32 sobre denominador 9 fim da fração reto T com reto c subscrito igual a numerador menos 21 vírgula 6.5 sobre denominador 9 fim da fração reto T com reto c subscrito igual a numerador menos 108 sobre denominador 9 fim da fração reto T com reto c subscrito igual a menos 12 espaço º reto C

Portanto, a temperatura, na escala Celsius, corresponde a - 12 ºC

Questão 7

(Aprendiz de Marinheiro - 2018) Três termômetros de mercúrio são colocados num mesmo líquido e, atingido o equilíbrio térmico, o graduado na escala Celsius registra 45 ºC. Os termômetros graduados nas escalas Kelvin e Fahrenheit, respectivamente, devem registrar que valores?

a) 218 K e 113 ºF
b) 318 K e 113 ºF
c) 318 K e 223 ºF
d) 588 K e 313 ºF
e) 628 K e 423 ºF

Resposta correta: b) 318 K e 113 ºF.

Para transformar a temperatura na escala Celsius para a escala Kelvin, usaremos a seguinte relação:

TK = TC + 273
TK = 45 + 273 = 318 K

A expressão para transformar da escala Celsius para a escala Fahrenheit é:

reto T com reto C subscrito sobre 5 igual a numerador reto T com reto F subscrito menos 32 sobre denominador 9 fim da fração

Substituindo o valor da temperatura em Celsius, temos:

45 sobre 5 igual a numerador reto T com reto F subscrito menos 32 sobre denominador 9 fim da fração reto T com reto F subscrito menos 32 igual a 9.9 reto T com reto F espaço subscrito fim do subscrito igual a 81 mais 32 reto T com reto F subscrito igual a 113 espaço º reto F

Portanto, os termômetros registram, respectivamente, os valores 318 K e 113 ºF.

Veja também: Calorimetria

Questão 8

(PUC/SP - 2018) Uma determinada massa de gás perfeito está contida em um recipiente de capacidade 10,0 litros, sob pressão de 3,5 atm e temperatura inicial de 25,0 ºC. Após sofrer uma transformação isocórica, sua pressão aumenta para 7,0 atm. Determine a variação de temperatura da massa de gás, nas escalas Celsius e Fahrenheit, respectivamente, devido a essa transformação.

a) 298 e 536,4.
b) 298 e 568,4.
c) 323 e 581,4.
d) 323 e 613,4.

Resposta correta: a) 298 e 536,4.

O gás sofreu uma transformação isocórica, isto é, seu volume permaneceu constante. Neste caso, usaremos a Lei de Charles-Gay Lussac, ou seja:

reto P sobre reto T igual a reto P com 0 subscrito sobre reto T com 0 subscrito

Essa relação é válida para temperaturas absolutas. Desta forma, antes de substituir os valores, devemos passar a temperatura que está em Celsius para Kelvin. Assim:

T0 = 25 + 273 = 298 K

Agora, podemos substituir:

7 sobre reto T igual a numerador 3 vírgula 5 sobre denominador 298 fim da fração reto T igual a numerador 7.298 sobre denominador 3 vírgula 5 fim da fração reto T igual a numerador 2086 sobre denominador 3 vírgula 5 fim da fração igual a 596 espaço reto K

Para calcular a variação de temperatura devemos fazer:

incremento reto T igual a 596 menos 298 igual a 298 espaço reto K

A variação de temperatura na escala Celsius é igual a variação de temperatura na escala Kelvin. Para encontrar a correspondente variação na escala Fahrenheit, vamos usar a seguinte relação:

numerador incremento reto T com reto C subscrito sobre denominador 5 fim da fração igual a numerador incremento reto T com reto F subscrito sobre denominador 9 fim da fração

Substituindo os valores, temos:

298 sobre 5 igual a numerador incremento reto T com reto F subscrito sobre denominador 9 fim da fração incremento reto T com reto F subscrito igual a numerador 298.9 sobre denominador 5 fim da fração igual a 536 vírgula 4 espaço º reto F

Devido a essa transformação, nas escalas Celsius e Fahrenheit, respectivamente, as temperaturas registradas são 298 e 536,4.

Questão 9

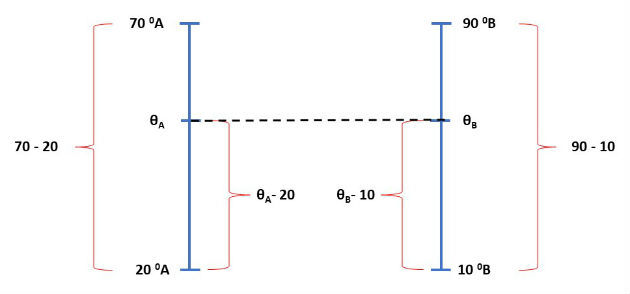
(Mackenzie - 2017) Uma escala termométrica A adota para a temperatura da água em ebulição à pressão normal, de 70 ºA, e para a temperatura de fusão do gelo à pressão normal, de 20 ºA. Outra escala termométrica B adota para a temperatura da água em ebulição à pressão normal, 90 ºB, e para a temperatura de fusão do gelo à pressão normal, de 10 ºB. A expressão que relaciona a temperatura das escalas A(θA) e B (θB) é

a) θB= 2,6.θA - 42
b) θB= 2,6.θA - 22
c) θB= 1,6.θA - 22
d) θB= 1,6.θA + 22
e) θB= 1,6.θA + 42

Resposta correta: c) θB= 1,6.θA - 22.

Podemos representar as duas escalas através do seguinte esquema:

Questão Mackenzie 2017 Temperatura

Os segmentos indicados na figura são proporcionais, logo podemos escrever a seguinte proporção:

numerador reto teta com reto A subscrito menos 20 sobre denominador 70 menos 20 fim da fração igual a numerador reto teta com reto B subscrito menos 10 sobre denominador 90 menos 10 fim da fração numerador reto teta com reto A subscrito menos 20 sobre denominador 50 fim da fração igual a numerador reto teta com reto B subscrito menos 10 sobre denominador 80 fim da fração 80 sobre 50. parêntese esquerdo reto teta com reto A subscrito menos 20 parêntese direito igual a reto teta com reto B subscrito menos 10 1 vírgula 6. parêntese esquerdo reto teta com reto A subscrito menos 20 parêntese direito igual a reto teta com reto B subscrito menos 10 reto teta com reto B subscrito igual a 1 vírgula 6 reto teta com reto A subscrito menos 32 mais 10 reto teta com reto B subscrito igual a 1 vírgula 6 reto teta com reto A subscrito menos 22

Portanto, a expressão que relaciona a temperatura das escalas A(θA) e B (θB) é θB= 1,6.θA - 22.

Questão 10

(Colégio Naval - 2016) Fossas abissais ou oceânicas são áreas deprimidas e profundas do piso submarino. A maior delas é a depressão Challenger, na Fossa das Marianas, com 11.033 metros de profundidade e temperatura da água variando entre 0 °C e 2 °C. De acordo com o texto, pode-se dizer que a pressão total sofrida por um corpo que esteja a uma altura de 33 m acima do solo dessa depressão e a variação de temperatura na escala absoluta (Kelvin) valem, respectivamente.

Dados: dágua = 1000 kg/m3; g = 10 m/s2; Patm = 1,0 . 105 N/m2

a) 1,101.108 N/m2 e 2 K.
b) 11,01.108 N/m2 e 2 K.
c) 1,101.108 N/m2 e 275 K.
d) 11,01.108 N/m2 e 275 K.
e) 110,1.108 N/m2 e 2 K.

Resposta correta: a) 1,101.108 N/m2 e 2 K.

Para encontrar o valor da pressão no ponto indicado, utilizaremos a seguinte fórmula da pressão hidrostática:

p = patm + dágua.g.h

Note que h, neste caso, é igual a profundidade no ponto considerado. O problema informa que a profundidade da depressão é de 11033 m, entretanto, o ponto está a 33 m acima do solo, logo:

h = 11 033 - 33 = 11 000 m

Transformando todos os valores para potência de 10 e substituindo na fórmula da pressão, temos:

p = 1.105 + 103 . 10 . 1,1 . 104
p = 1 . 105 + 1,1 . 108

Para efetuar a soma é necessário que os expoentes das potências sejam iguais, assim:

p = 0,001 . 108 + 1,1 . 108
p = 1,101 . 108 N/m2

A variação da temperatura na escala Kelvin, pode ser encontrada fazendo-se:

T1 = 0 + 273 = 273 K
T2 = 2 + 273 = 275 K
Δ T = 275 - 273 = 2 K

Perceba que a variação de temperatura na escala Celsius e na escala Kelvin são sempre iguais.

Portanto, a pressão total sofrida é de 1,101.108 N/m2 e a variação de temperatura é de 2 K.

Questão 11

(UERJ - 2015) No mapa abaixo, está representada a variação média da temperatura dos oceanos em um determinado mês do ano. Ao lado, encontra-se a escala, em graus Celsius, utilizada para a elaboração do mapa.

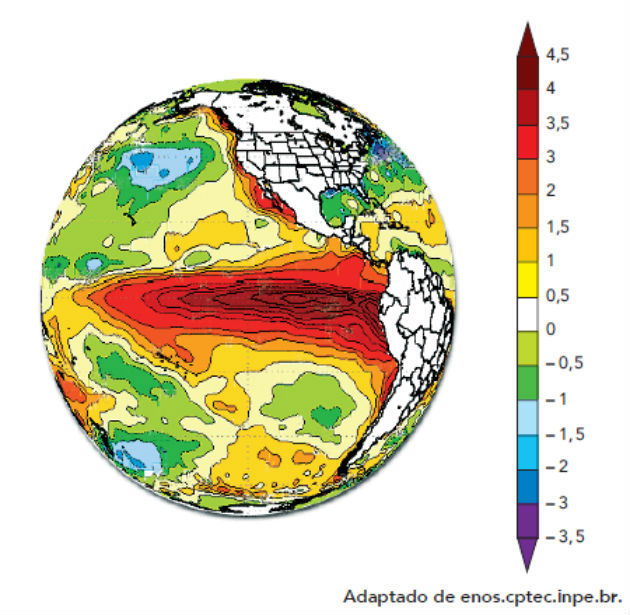
Questão UERJ 2015 temperatura

Determine, em graus Kelvin, o módulo da variação entre a maior e a menor temperatura da escala apresentada.

Resposta correta: 8 Kelvin.

Pelo mapa, concluímos que a menor temperatura é - 3,5 ºC e a maior é 4,5 ºC. Assim, o módulo da variação entre essas temperaturas será:

Δ T = 4,5 - (- 3,5) = 8 ºC

Conforme vimos na questão anterior, a variação de temperatura na escala Celsius e na escala Kelvin são iguais. Logo, o valor da variação da temperatura é igual a 8 K.

Questão 12

(UERJ - 2013) Observe na tabela os valores das temperaturas dos pontos críticos de fusão e de ebulição, respectivamente, do gelo e da água, à pressão de 1 atm, nas escalas Celsius e Kelvin.

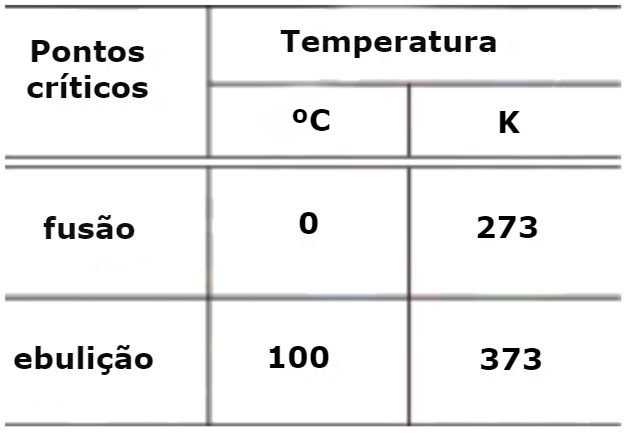
Questão de Temperatura UERJ 2013

Considere que, no intervalo de temperatura entre os pontos críticos do gelo e da água, o mercúrio em um termômetro apresenta uma dilatação linear.

Nesse termômetro, o valor na escala Celsius correspondente à temperatura de 313 K é igual a:

a) 20
b) 30
c) 40
d) 60

Resposta correta: c) 40.

Para transformar da escala Kelvin para a escala Celsius basta subtrair 273. Assim, a temperatura correspondente será:

313 - 273 = 40 ºC

Portanto, nesse termômetro, o valor na escala Celsius correspondente à temperatura de 313 K é igual a 40 ºC.

Questão 13

(Enem 2022 adaptada) A escala de temperatura Delisle (°D), inventada no século XVIII pelo astrônomo francês Joseph-Nicholas Delisle, a partir da construção de um termômetro, foi utilizada na Rússia no século XIX. A relação entre as temperaturas na escala Celsius (°C) e na escala Delisle está representada no gráfico pela reta que passa pelos pontos A e B.

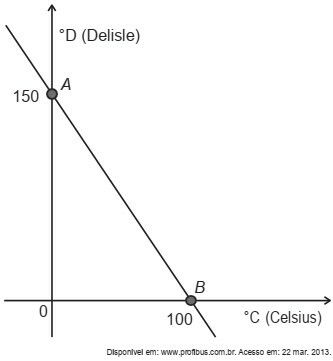
Gráfico escalas termométricas

Qual é a relação algébrica entre as temperaturas nessas duas escalas e para uma temperatura de 55ºC, qual a correspondente temperatura em ºD?

Resposta: a função é D = -1,5 + 150 e a temperatura correspondente é de 67,5 ºD.

1º passo: lei de formação da função.

A reta no gráfico demostra uma relação linear entre as duas escalas. A forma geral de uma função linear é:

reto y espaço igual a espaço ax espaço mais espaço reto b

Fazendo x como ºC e y como ºD, temos:

reto D espaço igual a espaço aC espaço mais espaço reto b

Onde a e b são números reais.

No gráfico temos dois pares ordenados (C, D): (100, 0) e (0, 150). Utilizando na função, podemos determinar os valores de a e b.

abre chaves atributos de tabela alinhamento de coluna left fim dos atributos linha com célula com reto I dois pontos espaço 0 espaço igual a espaço reto a.100 espaço mais espaço reto b espaço espaço fim da célula linha com célula com II dois pontos espaço 150 espaço igual a espaço reto a.0 espaço mais espaço reto b fim da célula fim da tabela fecha

Da equação II encontramos o valor de b

150 = b

Substituindo na equação I, temos:

0 espaço igual a espaço 100 reto a espaço mais espaço 150 menos 150 igual a 100 reto a numerador menos 150 sobre denominador 100 fim da fração igual a reto a menos 1 vírgula 5 igual a reto a

A lei da função fica:

reto D igual a menos 1 vírgula 5 reto C espaço mais espaço 150

2º passo: temperatura correspondente em ºD para 55 ºD.

Fazendo C = 55 na função:

reto D espaço igual a menos 1 vírgula 5 espaço. espaço 55 espaço mais espaço 150 reto D igual a menos 82 vírgula 5 espaço mais espaço 150 reto D igual a 67 vírgula 5

A temperatura correspondente para 55ºC em Delisle é de 67,5 ºD.

Questão 14

(SENAC-SP) A chegada do homem a lua aconteceu em 1969. A estrutura da lua é rochosa e praticamente não possui atmosfera, o que faz com que durante o dia a temperatura chegue a 105 °C e à noite caia para −155 °C.
Essa variação térmica, medida na escala Fahrenheit de temperatura, vale

a) 50.
b) 90.
c) 292.
d) 468.
e) 472.

Resposta: d) 468.

Para a menor temperatura

numerador º reto C sobre denominador 5 fim da fração igual a numerador º reto F menos 32 sobre denominador 9 fim da fração numerador menos 155 sobre denominador 5 fim da fração igual a numerador º reto F menos 32 sobre denominador 9 fim da fração menos 31 espaço. espaço 9 espaço igual a espaço º reto F menos 32 menos 279 igual a º reto F menos 32 menos 279 mais 32 igual a º reto F menos 247 igual a º reto F

Para a maior temperatura

105 sobre 5 igual a numerador º reto F menos 32 sobre denominador 9 fim da fração 21 espaço. espaço 9 espaço igual a espaço º reto F menos 32 189 espaço igual a º reto F menos 32 189 espaço mais espaço 32 igual a º reto F 221 igual a º reto F

Cálculo da variação térmica

221 - (-247) = 468

Questão 15

(PUC - SP 2015) O Slide, nome dado ao skate futurista, usa levitação magnética para se manter longe do chão e ainda ser capaz de carregar o peso de uma pessoa. É o mesmo princípio utilizado, por exemplo, pelos trens ultrarrápidos japoneses.

Para operar, o Slide deve ter a sua estrutura metálica interna resfriada a temperaturas baixíssimas, alcançadas com nitrogênio líquido. Daí a “fumaça” que se vê nas imagens, que, na verdade, é o nitrogênio vaporizando novamente devido à temperatura ambiente e que, para permanecer no estado líquido, deve ser mantido a aproximadamente –200 graus Celsius. Então, quando o nitrogênio acaba, o skate para de “voar”.

Imagem associada à questão

Com relação ao texto, a temperatura do nitrogênio o líquido, –200°C, que resfria a estrutura metálica interna do Slide, quando convertida para as escalas Fahrenheit e Kelvin, seria respectivamente:

a) –328 e 73
b) –392 e 73
c) –392 e –473
d) –328 e –73

Resposta: a) –328 e 73

Celsius para Farenheit

numerador º reto C sobre denominador 5 fim da fração igual a numerador º reto F menos 32 sobre denominador 9 fim da fração numerador menos 200 sobre denominador 5 fim da fração igual a numerador º reto F menos 32 sobre denominador 9 fim da fração menos 40 igual a numerador º reto F menos 32 sobre denominador 9 fim da fração menos 40 espaço. espaço 9 espaço igual a espaço º reto F menos 32 menos 360 igual a º reto F menos 32 menos 360 espaço mais espaço 32 igual a º reto F menos 328 igual a º reto F

Celsius para Kelvin

reto K igual a reto C espaço mais espaço 273 reto K igual a menos 200 espaço mais espaço 273 reto K igual a 73

Questão 16

Conteúdo exclusivo para assinantes Toda Matéria+
Além de mais exercícios, tenha acesso a mais recursos para dar um up nos seus estudos.
Corretor de Redação para o Enem
Exercícios exclusivos
Estude sem publicidade
Assinar Toda Matéria+

Veja também

Para mais exercícios de Física:

Exercícios de Física (resolvidos) para 2º ano do ensino médio

Rafael C. Asth
Rafael C. Asth
Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.
Veja também
Leitura Recomendada
Tópicos Relacionados
Exercícios Física Exercícios de Física 2º ano (Ensino Médio)
NOVIDADE Teste seus conhecimentos sobre Escalas Termométricas! Começar!