Exercícios sobre cinemática (questões resolvidas e comentadas)

Revisão por Rafael C. Asth

Professor de Matemática e Física

A cinemática é a área da Física que estuda o movimento sem, entretanto, considerar as causas deste movimento.

Neste ramo, estuda-se principalmente o movimento retilíneo uniforme, movimento retilíneo uniformemente acelerado e movimento circular uniforme.

Questão 1

Ana e Beatriz decidiram correr uma maratona no parque da cidade. Ana começou a correr às 8h da manhã com uma velocidade constante de 8 km/h. Beatriz, que estava um pouco atrasada, começou a correr 15 minutos depois, às 8h15min, mas com uma velocidade constante de 10 km/h. Suponha que ambas correm em linha reta na mesma direção. A que horas Beatriz alcançará Ana?

a) 8h45

b) 8h30

c) 9h00

d) 9h15

Questão 2

Mariana está viajando de carro em uma estrada reta e plana. Ela observa que a velocidade do seu carro aumenta de 20 m/s para 30 m/s em um intervalo de tempo de 10 segundos. Curiosa sobre o desempenho do veículo, ela decide calcular a aceleração média do carro durante esse intervalo de tempo.

Qual é a aceleração média do carro durante esse período?

a) 1m/s²

b) 2m/s²

c) 3m/s²

d) 5m/s²

Questão 3

(IFPR - 2018) Um veículo trafega a 108 km/h em uma autoestrada, onde a velocidade máxima permitida é 110 km/h. Ao tocar o telefone celular do condutor, imprudentemente ele desvia sua atenção para o aparelho ao longo de 4s. A distância percorrida pelo veículo durante os 4 s em que se movimentou sem a atenção do condutor, em m, foi igual a:

a) 132.
b) 146.
c) 168.
d) 120.

Ver Resposta

Alternativa correta: d) 120

Considerando que a velocidade do veículo permaneceu constante durante os 4s, usaremos a equação horária do movimento uniforme, ou seja:

s = s₀ + v.t

Antes de substituir os valores, precisamos transformar a unidade da velocidade de km/h para m/s. Para isso, basta dividir por 3,6:

v = 108 : 3,6 = 30 m/s

Substituindo os valores, encontramos:

s - s₀ = 30 . 4 = 120 m

Para saber mais, veja também: Movimento Uniforme

Questão 4

(PUC/SP - 2018) Por uma luva de redução de PVC, que fará parte de uma tubulação, passarão 180 litros de água por minuto. Os diâmetros internos dessa luva são 100 mm para a entrada e 60 mm para a saída da água.

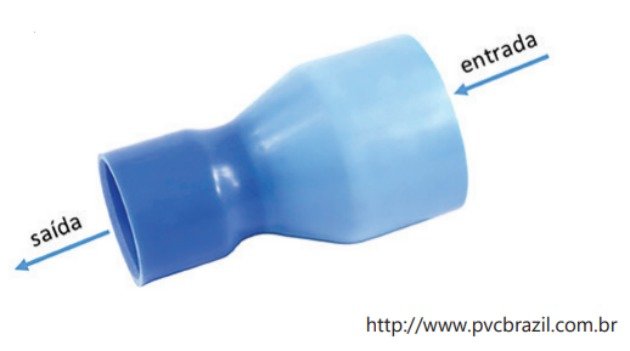
Determine, em m/s, a velocidade aproximada de saída da água por essa luva.

a) 0,8
b) 1,1
c) 1,8
d) 4,1

Ver Resposta

Alternativa correta: b) 1,1

Podemos calcular a vazão na tubulação dividindo o volume de líquido pelo tempo. Contudo, devemos passar as unidades para o sistema internacional de medidas.

Assim, teremos que transformar minutos em segundos e litros em metros cúbicos. Para isso, usaremos as seguintes relações:

1 minuto = 60 s
1 l = 1 dm³ = 0,001 m³⇒ 180 l = 0,18 m³

Agora, podemos calcular a vazão (Z):

$Z igual a numerador 0 vírgula 18 sobre denominador 60 fim da fração igual a 0 vírgula 003 espaço m ao cubo dividido por s$

Para encontrar o valor da velocidade de saída da água, vamos usar o fato da vazão ser igual a área da tubulação multiplicada pela velocidade, ou seja:

Z = A . v

Para fazer esse cálculo, precisamos primeiro conhecer o valor da área de saída e, para isso, usaremos a fórmula da área de um círculo:

A = π . R²

Sabemos que o diâmetro de saída é igual a 60 mm, então o raio será igual a 30 mm = 0,03 m. Considerando o valor aproximado de π = 3,1 e substituindo esses valores, temos:

A= 3,1 . (0,03)²= 0,00279 m²

Agora, podemos encontrar o valor da velocidade substituindo o valor da vazão e da área:

$0 vírgula 003 igual a 0 vírgula 00279. v v igual a numerador 0 vírgula 003 sobre denominador 0 vírgula 00279 fim da fração v aproximadamente igual 1 vírgula 1 m dividido por s$

Para saber mais, veja também: Fórmulas de Física

Questão 5

(PUC/RJ - 2017) A partir do solo, uma bola é lançada verticalmente com velocidade v e atinge uma altura máxima h. Se a velocidade de lançamento for aumentada em 3v, a nova altura máxima final atingida pela bola será: (Despreze a resistência do ar)

a) 2h
b) 4h
c) 8h
d) 9h
e) 16h

Ver Resposta

Alternativa correta: e) 16h

A altura atingida pela bola pode ser calculada utilizando a equação de Torricelli, ou seja:

v² = v₀² - 2.g.h

A aceleração da gravidade é negativa, pois a bola está subindo. Além disso, a velocidade quando a bola atinge a altura máxima é igual a zero.

Assim, na primeira situação temos que o valor de h será encontrado fazendo-se:

$0 igual a v ao quadrado menos 2. g. h espaço h igual a numerador v ao quadrado sobre denominador 2 g fim da fração$

Na segunda situação, a velocidade foi aumentada em 3v, ou seja, a velocidade do lançamento passou a ser de:

v₂ = v + 3v = 4v

Desta forma, na segunda situação a altura atingida pela bola será de:

$0 igual a v com 2 subscrito ao quadrado menos 2. g. h com 2 subscrito h com 2 subscrito igual a numerador v com 2 subscrito ao quadrado sobre denominador 2 g fim da fração h com 2 subscrito igual a numerador parêntese esquerdo 4 v parêntese direito ao quadrado sobre denominador 2 g fim da fração h com 2 subscrito igual a numerador 16 v ao quadrado sobre denominador 2 g fim da fração P o d e m o s espaço s u b s t i t u i r espaço numerador v ao quadrado sobre denominador 2 g fim da fração espaço p o r espaço h espaço n a espaço e x p r e s s ã o espaço a n t e r i o r vírgula espaço a s s i m dois pontos$

$h com 2 subscrito igual a 16 h$

Alternativa: e) 16h

Para saber mais, veja também: Movimento Retilíneo Uniformemente Variado

Questão 6

(UECE - 2016 - 2ª fase) Considere uma pedra em queda livre e uma criança em um carrossel que gira com velocidade angular constante. Sobre o movimento da pedra e da criança, é correto afirmar que

a) a aceleração da pedra varia e a criança gira com aceleração nula.
b) a pedra cai com aceleração nula e a criança gira com aceleração constante.
c) a aceleração em ambas é zero.
d) ambas sofrem acelerações de módulos constantes.

Ver Resposta

Alternativa correta: d) ambas sofrem acelerações de módulos constantes.

Tanto a velocidade quanto a aceleração são grandezas vetoriais, ou seja, são caracterizadas por módulo, direção e sentido.

Para que uma grandeza deste tipo sofra uma variação é necessário que pelo menos um desses atributos sofra modificações.

Quando um corpo está em queda livre o módulo da sua velocidade varia uniformemente, apresentando aceleração constante e igual a 9,8 m/s² (aceleração da gravidade).

Já no carrossel, o módulo da velocidade é constante, contudo, sua direção está variando. Neste caso, o corpo terá uma aceleração constante e que aponta para o centro da trajetória circular (centrípeta).

Veja também: Exercícios sobre Movimento Circular Uniforme

Questão 7

(UFLA - 2016) Uma pedra foi lançada verticalmente para cima. No momento em que ela está subindo, a

a) velocidade diminui e a aceleração diminui
b) velocidade diminui e a aceleração aumenta
c) velocidade é constante e a aceleração diminui
d) velocidade diminui e a aceleração é constante

Ver Resposta

Alternativa correta: d) velocidade diminui e a aceleração é constante

Um corpo ao ser lançado verticalmente para cima, próximo à superfície da terra, sofre a atuação de uma força gravitacional.

Esta força lhe imprime uma aceleração constante de módulo igual a 9,8 m/s² , direção vertical e sentido para baixo. Desta maneira, o módulo da velocidade vai diminuindo até que atinja o valor igual a zero.

Questão 8

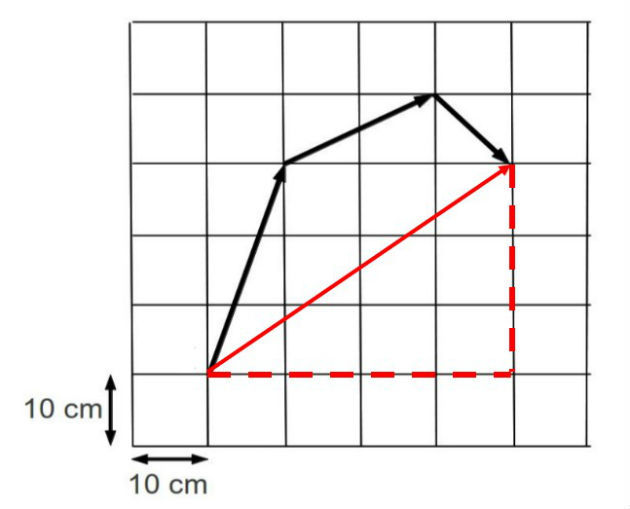
(UFLA - 2016) A figura em escala mostra os vetores de deslocamento de uma formiga, que saindo do ponto I, chegou ao ponto F, após 3 min e 20 s. O módulo do vetor velocidade média do movimento da formiga nesse trajeto foi de:

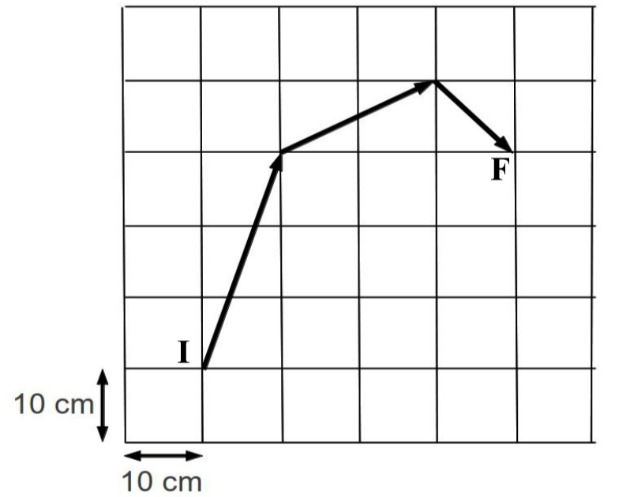
a) 0,15 cm/s
b) 0,25 cm/s
c) 0,30 cm/s
d) 0,50 cm/s

Ver Resposta

Alternativa correta: b) 0,25 cm/s

O módulo do vetor velocidade média é encontrado calculando-se a razão entre o módulo do vetor deslocamento e o tempo.

Para encontrar o vetor deslocamento, devemos ligar o ponto inicial ao ponto final da trajetória da formiga, conforme representado na imagem abaixo:

Note que o seu módulo pode ser encontrado fazendo-se o teorema de Pitágoras, pois o comprimento do vetor é igual a hipotenusa do triângulo assinalado.

Antes de encontrarmos a velocidade, devemos transformar o tempo de minutos para segundos. Sendo 1 minuto igual a 60 segundos, temos:

t = 3 . 60 + 20 = 180 + 20 = 200 s

Agora, podemos encontrar o módulo da velocidade fazendo:

$v igual a 50 sobre 200 igual a 0 vírgula 25 espaço c m dividido por s$

Veja também: Cinemática

Questão 9

(IFMG - 2016) Em função de um grave acidente ocorrido em uma barragem de rejeitos de minério, uma primeira onda desses rejeitos, mais rápida, invadiu uma bacia hidrográfica. Uma estimativa para o tamanho dessa onda é de 20 km de extensão. Um trecho urbano dessa bacia hidrográfica possui cerca de 25 km. Supondo neste caso que a velocidade média com que a onda passa pela calha do rio é de 0,25 m/s, o tempo de passagem total da onda pela cidade, contado a partir da chegada da onda no trecho urbano, é de:

a) 10 horas
b) 50 horas
c) 80 horas
d) 20 horas

Ver Resposta

Alternativa correta: b) 50 horas

A distância percorrida pela onda será igual a 45 km, ou seja, a medida da sua extensão (20 km) mais a extensão da cidade (25 km).

Para encontrar o tempo de passagem total usaremos a fórmula da velocidade média, assim:

$v com m subscrito igual a numerador incremento s sobre denominador t fim da fração$

Contudo, antes de substituir os valores, devemos transformar a unidade de velocidade para km/h, assim, o resultado encontrado para o tempo estará em horas, conforme indicado nas opções.

Fazendo essa transformação temos:

v_m = 0,25 . 3,6 = 0,9 km/h

Substituindo os valores na fórmula de velocidade média, encontramos:

$0 vírgula 9 igual a 45 sobre t t igual a numerador 45 sobre denominador 0 vírgula 9 fim da fração igual a 50 espaço h o r a s$

Questão 10

(UFLA - 2015) A descarga atmosférica é um fenômeno natural complexo, com muitos aspectos ainda desconhecidos. Um desses aspectos, pouco visível, ocorre no início da propagação da descarga. A descarga da nuvem para o solo inicia-se num processo de ionização do ar a partir da base da nuvem e propaga-se em etapas denominadas passos consecutivos. Uma câmera de alta velocidade de captura de quadros por segundo identificou 8 passos, de 50 m cada um, para uma descarga específica, com registros de intervalo de tempo de 5,0 x 10^-4 segundos por passo. A velocidade média de propagação da descarga, nesta etapa inicial denominada de líder escalonado, é de

a) 1,0 x 10^-4 m/s
b) 1,0 x 10⁵ m/s
c) 8,0 x 10⁵ m/s
d) 8,0 x 10^-4 m/s

Ver Resposta

Alternativa correta: b) 1,0 x 10⁵ m/s

A velocidade média de propagação será encontrada fazendo-se:

$v com m subscrito igual a numerador incremento s sobre denominador t fim da fração$

Para encontrar o valor de Δs, basta multiplicar 8 por 50 m, pois são 8 passos com 50 m cada um. Assim:

Δs = 50 . 8 = 400 m.

Como o intervalo entre cada passo é de 5,0 . 10^-4 s, para 8 passos o tempo será igual a:

t = 8 . 5,0 . 10^-4 = 40 . 10^-4 = 4 . 10^-3 s

$v com m subscrito igual a numerador 400 sobre denominador 4.10 à potência de menos 3 fim do exponencial fim da fração v com m subscrito igual a numerador 4.10 ao quadrado sobre denominador 4.10 à potência de menos 3 fim do exponencial fim da fração igual a 1.10 à potência de 5 espaço m dividido por s$

Você também pode se interessar por:

Veja mais exercícios de Física (resolvidos) para 1º ano do ensino médio.

Revisão por Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Edição por Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.