Força resultante: o que é, como calcular e exercícios

Rafael C. Asth

Professor de Matemática e Física

A força resultante equivale a todas as forças que atuam em um corpo, tanto em intensidade quanto em direção e sentido. Ela é uma ação imaginária que substitui todas as outras forças, produzindo o mesmo efeito.

Em um corpo onde atuam as forças: e , a resultante das forças é igual a:

Assim, a força resultante é a soma das forças aplicadas ao corpo, e seu estado, estar parado ou em movimento, é efeito da força resultante.

Portanto, não se trata de mais uma força produzida por um agente externo, como um puxão ou empurrão, mas sim do efeito já produzido pelas forças.

Toda força é uma grandeza vetorial, ou seja, possui valor (intensidade, módulo), direção e sentido. Ao somarmos as forças que atuam no corpo, devemos considerar não só seus valores, mas também suas direções e os sentidos.

Há duas formas de encontrarmos a força resultante: pela soma vetorial das forças individuais ou pela segunda Lei de Newton.

Segunda Lei de Newton

A segunda Lei de Newton diz que a força resultante é proporcional à aceleração produzida por ela. Tanto a força resultante quanto a aceleração possuem a mesma direção e o mesmo sentido.

Matematicamente, a força resultante é, conforme a segunda Lei de Newton, o produto entre a massa do corpo e sua aceleração.

Onde,

é a força resultante, medida em Newtons (N),
m é a massa, em quilogramas (kg),
a é a aceleração, em metros por segundo ao quadrado .

Exemplo
Um corpo com a massa de 5 kg cai de uma janela do terceiro andar de um prédio. Este corpo se mantém com uma aceleração de 9,81 m/s². Qual a intensidade, a direção e o sentido da força que produz o movimento?

O movimento se mantém na direção vertical com sentido apontado para o centro da Terra. A força que age sobre o corpo é a força da gravidade. Desprezando a resistência do ar, a gravidade é a única força que atua no movimento, sendo a força resultante.

A intensidade da força pode ser calculada pela segunda Lei de Newton:

Cálculo da força resultante pela soma vetorial

As direções e os sentidos nos indicam quais operações devemos realizar a fim de determinar a força resultante. Se as forças atuam com a mesma direção e o mesmo sentido, elas devem ser somadas; se estão na mesma direção, mas em sentidos opostos, devem ser subtraídas. As setas são os vetores que representam as forças.

Mesma direção e mesmo sentido:

Os módulos são somados.

2 N + 4 N = 6 N

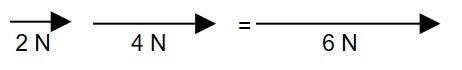
Mesma direção, mas em sentidos opostos:

Os módulos são subtraídos.

2 N - 4 N = - 2 N

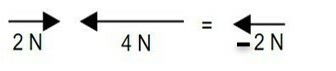
O sinal negativo se refere ao sentido. Adotando o sentido para a direita como positivo, a resultante aponta para a esquerda.

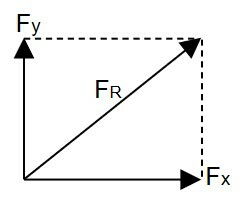
Soma de vetores perpendiculares (90º)

Caso duas forças perpendiculares atuem em um corpo, seu módulo é determinado pelo Teorema de Pitágoras.

Forças oblíquas

Forças oblíquas são forças em que suas direções realizam um certo ângulo entre si, que difira de 90º. Quando forças oblíquas atuam sobre o corpo, determinamos seu módulo, sua direção e seu sentido pela regra do paralelogramo.

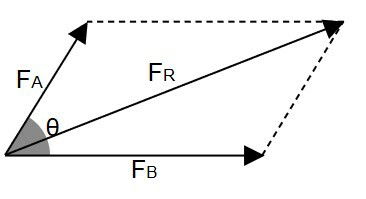
Para determinar direção e sentido, traçamos retas paralelas à cada vetor de força, como as linhas pontilhadas na figura. O vetor resultante começa no ponto de atuação das forças e termina na interseção das linhas paralelas.

Neste caso, o módulo é dado por:

Aprenda mais sobre operações com vetores.

Força resultante zero ou nula

Após as forças serem somadas, em muitos casos, a força resultante é nula, ou seja, seu módulo (valor) é zero. Nestes casos, existem duas possibilidades:

1. O corpo está parado. Este estado recebe o nome de equilíbrio estático.

2. O corpo está em movimento retilíneo uniforme (MRU), conhecido como equilíbrio dinâmico. Neste caso, o movimento se dá por inércia e não pela ação das forças.

Veja também:

• Força
• Segunda Lei de Newton
• Leis de Newton
• Exercícios sobre força de tração
• Exercícios sobre a segunda lei de newton (com respostas explicadas)

Exercícios sobre força resultante

Exercício 1

Em uma competição esportiva estudantil, dois times disputam a prova do cabo de guerra. Os times puxam uma corda na mesma direção, mas em sentidos contrários. O objetivo é trazer um ponto demarcado na corda até um certo referencial.

Suponha que o time A esteja produzindo uma força de 110 N, para a esquerda; enquanto o time B, 105 N para a direita. Calcule a força resultante e determine qual é o time vencedor.

Exercício 2

Uma criança brinca puxando um carrinho de brinquedo preso por um barbante. O carrinho se movimenta pelo chão enquanto a força produzida pela criança atua na direção do barbante. Suponha que as competentes vertical e horizontal da força sejam conhecidas e iguais a 0,3 N e 0,4 N. Determine o módulo da força resultante produzida pela criança.

Exercício 3

Uma bola de boliche de massa igual a 5 kg é arremessada em direção aos pinos. Ao sair das mãos do jogador, ela desenvolve uma aceleração de 0,75 m/s². Qual o módulo da força resultante aplicada à bola?

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.