Exercícios sobre energia potencial e cinética
Estude sobre energia cinética e potencial com esta lista de exercícios resolvidos que o Toda Matéria preparou para você. Tire suas dúvidas com as resoluções passo a passo e se prepare com as questões do ENEM e vestibulares.
Questão 1
Em um mercado, dois trabalhadores estão fazendo o carregamento de um caminhão que entregará hortaliças. A operação acontece do seguinte modo: o trabalhador 1 retira as hortaliças de uma banca e os guarda em uma caixa de madeira. Após, arremessa a caixa a fazendo deslizar sobre o chão, em direção ao trabalhador 2 que está ao lado do caminhão, encarregado de guardá-la sobre a carroceria.
O trabalhador 1 lança a caixa com uma velocidade inicial de 2 m/s e a força de atrito realiza um trabalho de módulo igual a -12 J. O conjunto caixa de madeira mais hortaliças, possui uma massa de 8 kg.
Nessa condições, é correto afirmar que a velocidade com que a caixa chega ao trabalhador 2, é de
a) 0,5 m/s.
b) 1 m/s.
c) 1,5 m/s.
d) 2 m/s.
e) 2,5 m/s.
Questão 2
Em um depósito de grãos ensacados uma grande estante com quatro prateleiras de 1,5 m de altura armazena a mercadoria que será despachada. Ainda no solo, seis sacos de grãos com 20 kg cada, são arrumados sobre um palet de madeira, que é recolhido por uma empilhadeira. Cada palet possui 5 kg de massa.

Considerando a aceleração da gravidade igual 10 m/s², o conjunto sacos mais palet como um corpo e desprezando suas dimensões, a energia potencial gravitacional adquirida pelo conjunto palet mais sacos de grãos, ao saírem do chão e serem guardados no quarto andar da estante, corresponde a
a) 5 400 J.
b) 4 300 J.
c) 5 625 J.
d) 7 200 J.
e) 7 500 J.
Questão 3
Uma mola que possui um comprimento de 8 cm quando em repouso, recebe uma carga de compressão. Um corpo de massa de 80 g é colocado sobre a mola e seu comprimento diminui para 5 cm. Considerando a aceleração da gravidade como 10 m/s² determine:
a) A força que age sobre a mola.
b) A constante elástica da mola.
c) A energia potencial armazenada pela mola.
Questão 4
Um corpo de massa igual a 3 kg é abandonado em queda livre de uma altura de 60 m. Determine a energia mecânica, cinética e potencial nos instantes t = 0 e t = 1s. Considere g = 10 m/s².
Questão 5
Uma criança está brincando em um balanço de um parque com seu pai. Em determinado momento o pai puxa o balanço, o erguendo a uma altura de 1,5 m em relação ao ponto em que se encontra quando em repouso. O conjunto balanço mais criança possui a massa igual a 35 kg. Determine a velocidade horizontal do balanço ao passar pela parte mais baixa da trajetória.
Considere um sistema conservativo onde não há perdas de energia e a aceleração da gravidade é igual a 10 m/s².
Questão 6
(Enem 2019) Numa feira de ciências, um estudante utilizará o disco de Maxwell (ioiô) para demonstrar o princípio da conservação da energia. A apresentação consistirá em duas etapas:
Etapa 1 - a explicação de que, à medida que o disco desce, parte de sua energia potencial gravitacional é transformada em energia cinética de translação e energia cinética de rotação;
Etapa 2 - o cálculo da energia cinética de rotação do disco no ponto mais baixo de sua trajetória, supondo o sistema conservativo.
Ao preparar a segunda etapa, ele considera a aceleração da gravidade igual a 10 m/s² e a velocidade linear do centro de massa do disco desprezível em comparação com a velocidade angular. Em seguida, mede a altura do topo do disco em relação ao chão no ponto mais baixo de sua trajetória, obtendo 1/3 da altura da haste do brinquedo.
As especificações de tamanho do brinquedo, isto é, de comprimento (C), largura (L) e altura (A), assim como da massa de seu disco de metal, foram encontradas pelo estudante no recorte de manual ilustrado a seguir.
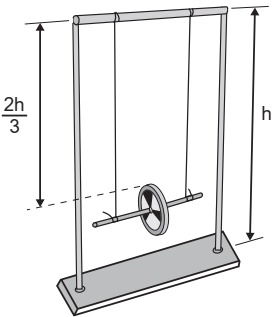
Conteúdo: base de metal, hastes metálicas, barra superior, disco de metal.
Tamanho (C × L × A): 300 mm × 100 mm × 410 mm
Massa do disco de metal: 30 g
O resultado do cálculo da etapa 2, em joule, é:
Questão 7
(CBM-SC 2018) A energia cinética é a energia devida ao movimento. Tudo que se move tem energia cinética. Logo, os corpos em movimento possuem energia e, portanto, podem causar deformações. A energia cinética de um corpo depende da sua massa e da sua velocidade. Portanto, podemos afirmar que a energia cinética constitui uma função da massa e da velocidade de um corpo, em que energia cinética é igual à metade da massa vezes sua velocidade ao quadrado. Se fizermos alguns cálculos, verificaremos que a velocidade determina um aumento muito maior da energia cinética do que a massa, assim podemos concluir que haverá lesões muito maiores nos ocupantes de um veículo envolvido em um acidente de alta velocidade do que naqueles em um acidente de baixa velocidade.
Sabe-se que dois automóveis, ambos com 1500 kg, colidem numa mesma barreira. O automóvel A possui uma velocidade de 20 m/s e o veículo B uma velocidade de 35 m/s. Qual veículo estará mais suscetível a sofrer uma colisão mais violenta e por quê?
a) Veículo A, pois ele possui uma velocidade superior à do veículo B.
b) Veículo B, pois ele possui uma velocidade constante superior à do o veículo A.
c) Veículo A, pois ele possui a mesma massa que o veículo B, entretanto possui uma velocidade constante superior à do veículo B.
d) Ambos os veículos sofrerão o impacto com as mesmas intensidades.
Questão 8
(Enem 2005) Observe a situação descrita na tirinha abaixo.



Assim que o menino lança a flecha, há transformação de um tipo de energia em outra. A transformação, nesse caso, é de energia
a) potencial elástica em energia gravitacional.
b) gravitacional em energia potencial.
c) potencial elástica em energia cinética.
d) cinética em energia potencial elástica.
e) gravitacional em energia cinética
Questão 9
(Enem 2012) Um automóvel, em movimento uniforme, anda por uma estrada plana, quando começa a descer uma ladeira, na qual o motorista faz com que o carro se mantenha sempre com velocidade escalar constante.
Durante a descida, o que ocorre com as energias potencial, cinética e mecânica do carro?
a) A energia mecânica mantém-se constante, já que a velocidade escalar não varia e, portanto, a energia cinética é constante.
b) A energia cinética aumenta, pois a energia potencial gravitacional diminui e quando uma se reduz, a outra cresce.
c) A energia potencial gravitacional mantém-se constante, já que há apenas forças conservativas agindo sobre o carro.
d) A energia mecânica diminui, pois a energia cinética se mantém constante, mas a energia potencial gravitacional diminui.
e) A energia cinética mantém-se constante, já que não há trabalho realizado sobre o carro.
Questão 10
(FUVEST 2016) Helena, cuja massa é 50 kg, pratica o esporte radical bungee jumping. Em um treino, ela se solta da beirada de um viaduto, com velocidade inicial nula, presa a uma faixa elástica de comprimento natural e constante elástica k = 250 N/m. Quando a faixa está esticada 10 m além de seu comprimento natural, o módulo da velocidade de Helena é
Note e adote: aceleração da gravidade: 10 m/s² . A faixa é perfeitamente elástica; sua massa e efeitos dissipativos devem ser ignorados.
a) 0 m/s
b) 5 m/s
c) 10 m/s
d) 15 m/s
e) 20 m/s
Questão 11
(USP 2018) Dois corpos de massas iguais são soltos, ao mesmo tempo, a partir do repouso, da altura h1 e percorrem os diferentes trajetos (A) e (B), mostrados na figura, onde x1 > x2 e h1 > h2.

Considere as seguintes afirmações:
I. As energias cinéticas finais dos corpos em (A) e em (B) são diferentes.
II. As energias mecânicas dos corpos, logo antes de começarem a subir a rampa, são iguais.
III. O tempo para completar o percurso independe da trajetória.
IV. O corpo em (B) chega primeiro ao final da trajetória.
V. O trabalho realizado pela força peso é o mesmo nos dois casos.
É correto somente o que se afirma em
Note e adote: Desconsidere forças dissipativas.
a) I e III.
b) II e V.
c) IV e V.
d) II e III.
e) I e V.
Você continuar praticando com:
Você pode se interessar por
ASTH, Rafael. Exercícios sobre energia potencial e cinética. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-energia-potencial-cinetica/. Acesso em:



