Lei de Biot-Savart: o que é, qual a fórmula e como se calcula

A Lei de Biot-Savart nos diz como um fio percorrido por uma corrente elétrica constante no tempo produz um campo magnético no espaço a seu redor.

Essa lei foi desenvolvida pelos físicos Jean-Baptiste Biot e Félix Savart logo após a experiência realizada por Hans Christian Oersted em 1820 que mostrou que correntes elétricas criam campos magnéticos ao seu redor ao aproximar uma bússola de um fio condutor sujeito a uma corrente.

A fórmula geral da Lei de Biot-Savart

A equação geral da Lei de Biot-Savart permite determinar o campo magnético B gerado por uma corrente elétrica (I) em qualquer ponto P do espaço que se encontra à distância (r) de um fio condutor, conforme mostrado na figura abaixo:

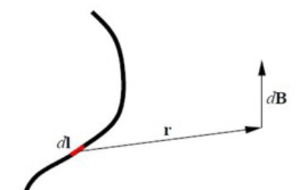
Como o campo magnético é uma grandeza vetorial, sua determinação envolve conhecer sua direção, sentido e módulo.

Ela é expressa pela fórmula:

Ela também pode ser expressa como:

Onde:

• dB é o campo magnético infinitesimal (extremamente pequeno) criado por um elemento de corrente;
• μ₀ é a permeabilidade magnética do vácuo igual a μ₀ = 4π × 10⁻⁷ Tm/A;
• I é a corrente elétrica constante que passa pelo fio (em ampères);
• dℓ é um elemento infinitesimal de comprimento do fio;
• θ é o ângulo entre o elemento de corrente (dℓ) e o vetor que liga esse elemento ao ponto onde queremos calcular o campo;
• r é a distância do elemento de corrente até o ponto onde calculamos o campo.

Observe primeiro que a lei geral não traz nenhuma informação sobre a forma do fio, que pode ser reto, curvo, espiral etc. Atente que ela envolve elementos infinitesimais ou extremamente pequenos.

Para resolvê-la é necessário o conhecimento de cálculo integral e diferencial. Como é uma matemática mais complexa, damos abaixo a equação de Biot-Savart para casos especiais: primeiro aplicada à uma carga em movimento e depois em diferentes formatos do fio, a saber, fio reto, espira circular e bobina, e solenoide.

Aplicação da Lei de Biot-Savart em uma carga elétrica em movimento

Essa lei diz que uma carga elétrica em movimento produz ao seu redor um campo magnético, cuja intensidade é igual a:

Onde:

• B é o módulo do campo magnético em Tesla (T);
• μ₀ é a permeabilidade magnética do vácuo igual a μ₀ = 4π × 10⁻⁷ Tm/A;
• |q| é o módulo da carga elétrica em Coulomb (C);
• v é a velocidade da partícula em m/s;
• r é a distância da partícula até o ponto em que se deseja medir o campo magnético em metros (m);
• θ é o ângulo formado ente e .

Aplicação da Lei de Biot-Savart em um fio condutor retilíneo infinito

Para calcular o campo magnético a uma distância de um fio retilíneo muito longo percorrido por uma corrente constante , usamos a lei na seguinte forma:

Onde:

• μ₀ é a permeabilidade magnética do vácuo igual a μ₀ = 4π × 10⁻⁷ Tm/A;
• I é a corrente elétrica constante que atravessa o solenoide;
• r é a distância entre o fio condutor e o ponto onde se quer saber o valor do campo magnético.

Observe que:

• Essa equação da Lei de Biot-Savart não possui nenhum elemento infinitesimal (precedido pela letra d), isso porque ela é fruto da integração da lei geral;
• O campo magnético é inversamente proporcional à distância r;
• O campo magnético é diretamente proporcional à corrente elétrica;
• O campo magnético é medido em Testa (T).

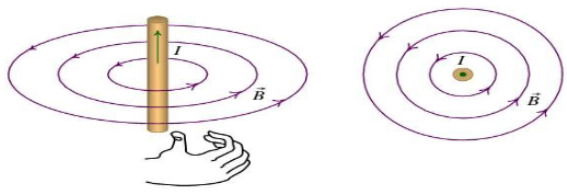
A direção e sentido do campo magnético são encontrados segundo a regra da mão direita, onde o dedão se alinha à direção e sentido da corrente e os outros quatro dedos apontam na direção e sentido do campo magnético.

Por convenção o campo magnético cujo sentido é saindo do papel é representado por um círculo com um ponto no centro (), como no lado direito da figura abaixo.

Quando o sentido do campo magnético é entrando no papel, ele é representando por um círculo com um x no centro ou .

Aplicação da Lei de Biot-Savart em uma espira circular

Uma espira circular nada mais é do que um fio que possui a forma de um círculo.

Quando a espira de raio for percorrida por uma corrente elétrica constante, surgirá um campo magnético no espaço ao redor da espira. O módulo do campo magnético será:

Onde:

• μ₀ é a permeabilidade magnética do vácuo igual a μ₀ = 4π × 10⁻⁷ Tm/A;
• I é a corrente elétrica constante que atravessa o solenoide;
• R é o raio da espira circular.

Suas linhas de campo terão as direções e sentidos mostrados na figura abaixo:

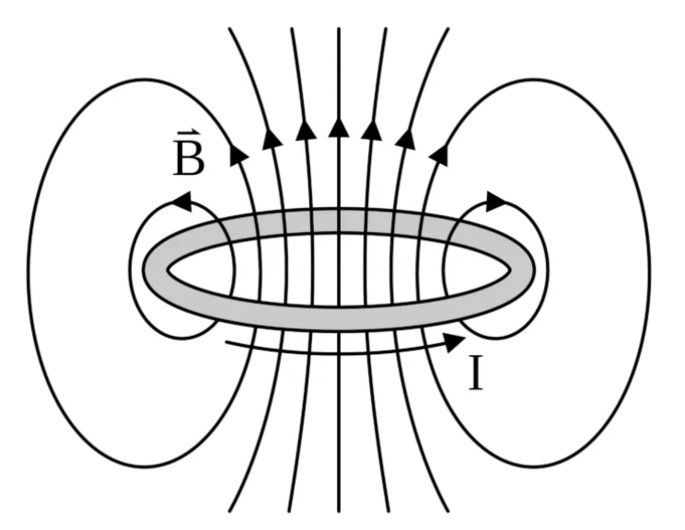
Quando tivermos um conjunto de N espiras sobrepostas formando uma bobina, o campo magnético será dado pela multiplicação da quantidade de espiras pelo campo magnético produzido por uma única espira, ou:

O campo magnético terá mesma direção e sentido do mostrado para uma única espira, mas será mais intenso:

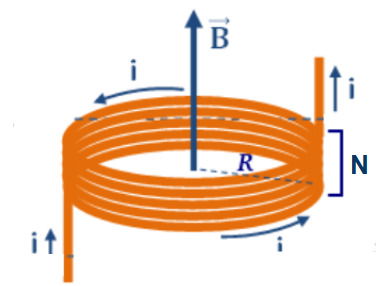
Aplicação da Lei de Biot-Savart para um solenoide

Um solenoide é um conjunto de várias espiras arranjadas em espiral, formando uma estrutura helicoidal com largura l.

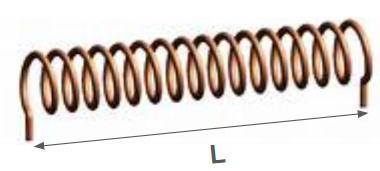
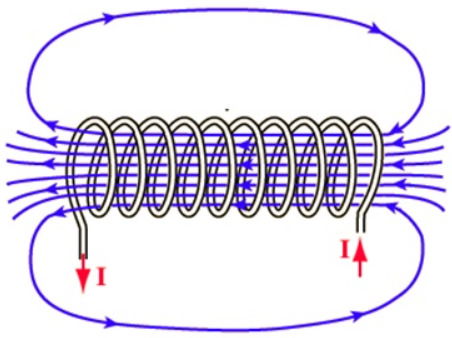
Os campos magnéticos gerados por cada um dos ciclos da espiral se somam e formam um campo magnético resultante muito semelhante ao campo magnético de um ímã. Seu módulo é:

Onde:

• N é o número de voltas do solenoide;
• μ₀ é a permeabilidade magnética do vácuo igual a μ₀ = 4π × 10⁻⁷ Tm/A;
• I é a corrente elétrica constante que atravessa o solenoide;
• L é a largura total do solenoide.

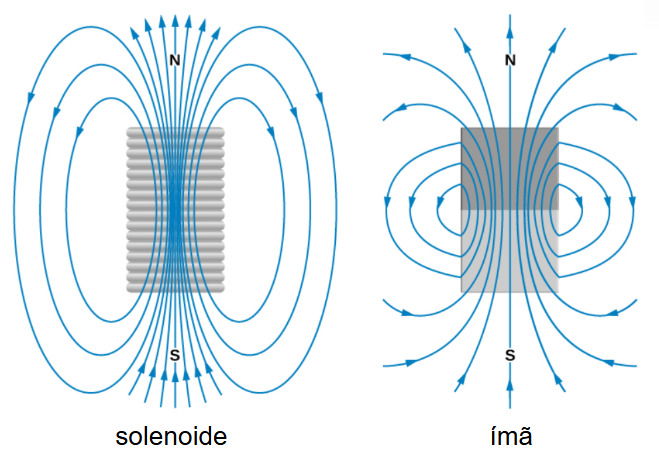
Como o campo magnético de um solenoide por onde passa uma corrente elétrica constante é muito semelhante ao campo gerado por um ímã ele é chamado de eletroímã. Compare abaixo os campos gerados pelo solenoide e pelo ímã:

Resumo dos casos especiais da Lei de Biot-Savart

No quadro abaixo mostramos a forma da Lei de Biot-Savart para os casos mais simples:

Caso especial	Fórmula de Biot-Savart
Carga elétrica em movimento
Fio retilíneo
Espira circular
Solenoide

Exemplo:

Para um fio percorrido por uma corrente elétrica constante igual a 10 A, o campo magnético a uma distância de 2 cm é:

B = (4π × 10⁻⁷ × 10) / (2π × 0,02)

B = 10⁻⁴ T = 100 μT

Considerações finais da Lei de Biot-Savart

A Lei de Biot-Savart ajuda a projetar as bobinas que criam os campos magnéticos nos motores elétricos, nos carregadores de celular sem fio e nos detetores de metal, entre outros.

Compreender esta lei é essencial para entender o funcionamento de praticamente todos os dispositivos eletromagnéticos modernos, desde o motor do ventilador até os aceleradores de partículas mais avançados do mundo.

Confira os exercícios sobre magnetismo (com respostas explicadas).