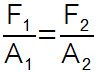Princípio de Pascal

Rosimar Gouveia

Professora de Matemática e Física

O Princípio de Pascal é uma lei da hidrostática que envolve a variação de pressão hidráulica num fluido em equilíbrio.

Recebe esse nome pois foi elaborada no século XVII pelo físico, matemático e filósofo francês Blaise Pascal (1623-1662).

Seu enunciado é expresso da seguinte maneira:

“O aumento da pressão exercida em um líquido em equilíbrio é transmitido integralmente a todos os pontos do líquido bem como às paredes do recipiente em que ele está contido.”

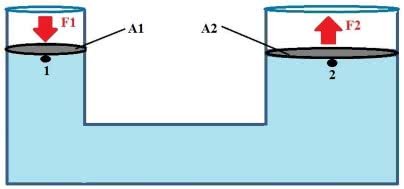
Fórmula

A partir da figura acima, a fórmula do Princípio de Pascal é expressa:

Onde,

F₁ e F₂: forças aplicadas aos êmbolos 1 e 2
A₁ e A₂: áreas dos êmbolos 1 e 2

Nesse sentido, as intensidades das forças aplicadas são diretamente proporcionais às áreas dos êmbolos.

Aplicações: Exemplos

Alguns exemplos sobre o Princípio de Pascal podem ser aplicados em:

• Prensas hidráulicas
• Elevadores hidráulicos
• Freios hidráulicos
• Barragens
• Caixas d’água
• Sistemas de amortecedores

Princípio de Stevin

O Teorema de Stevin é conhecido com Lei Fundamental da Hidrostática. Seu enunciado é:

“A diferença entre as pressões de dois pontos de um fluido em equilíbrio (repouso) é igual ao produto entre a densidade do fluido, a aceleração da gravidade e a diferença entre as profundidades dos pontos.”

Sendo assim, esse teorema determina a variação da pressão hidrostática que ocorre nos fluidos.

Para calcular essa variação utiliza-se a seguinte fórmula:

∆P = γ ⋅ ∆h ou ∆P = d.g. ∆h

Onde,

∆P: variação da pressão hidrostática (Pa)
γ: peso específico do fluido (N/m³)
d: densidade (Kg/m³)
g: aceleração da gravidade (m/s²)
∆h: variação da altura da coluna de líquido (m)

Princípio de Arquimedes

Além do Princípio de Pascal e de Stevin, o Teorema de Arquimedes também faz parte da hidrostática. Seu enunciado é:

“Todo corpo mergulhado num fluido recebe um impulso de baixo para cima igual ao peso do volume do fluido deslocado, por esse motivo, os corpos mais densos que a água, afundam, enquanto os menos densos flutuam.”

Esse teorema é utilizado para calcular a força vertical e para cima (força empuxo) que torna um corpo mais leve no interior de um fluido.

Para calcular a força empuxo, utiliza-se a seguinte fórmula:

E= d_f.V_fd.g

Onde,

E: força empuxo (N)
d_f: densidade do fluido (kg/m³)
V_fd: volume do fluido deslocado (m³)
g: Aceleração da gravidade (m/s²)

Leia também: Hidrostática e Fórmulas de Física.

Exercícios de Vestibular com Gabarito

1. (UNICAMP) A figura abaixo mostra, de forma simplificada, o sistema de freios a disco de um automóvel.

Ao se pressionar o pedal do freio, este empurra o êmbolo de um primeiro pistão que, por sua vez, através do óleo do circuito hidráulico, empurra um segundo pistão.

O segundo pistão pressiona uma pastilha de freio contra um disco metálico preso à roda, fazendo com que ela diminua sua velocidade angular.

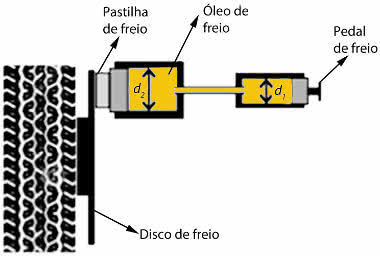
Considerando o diâmetro d2 do segundo pistão duas vezes maior que o diâmetro d1 do primeiro, qual a razão entre a força aplicada ao pedal de freio pelo pé do motorista e a força aplicada à pastilha de freio?

a) 1/4
b) 1/2
c) 2
d) 4

2. (UERJ) Observe, na figura a seguir, a representação de uma prensa hidráulica, na qual as forças F1 e F2 atuam, respectivamente, sobre os êmbolos dos cilindros I e II.

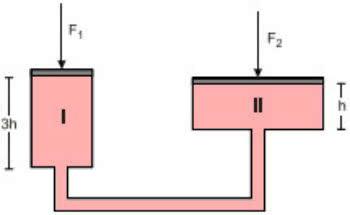
Admita que os cilindros estejam totalmente preenchidos por um líquido. O volume do cilindro II é igual a quatro vezes o volume do cilindro I, cuja altura é o triplo da altura do cilindro II. A razão entre as intensidades das forças F2 e F1, quando o sistema está em equilíbrio, corresponde a:

a) 12
b) 6
c) 3
d) 2

3. (Enem 2013) Para oferecer acessibilidade aos portadores de dificuldades de locomoção, é utilizado, em ônibus e automóveis, o elevador hidráulico.

Nesse dispositivo é usada uma bomba elétrica, para forçar um fluido a passar de uma tubulação estreita para outra mais larga, e dessa forma acionar um pistão que movimenta a plataforma.

Considere um elevador hidráulico cuja área da cabeça do pistão seja cinco vezes maior do que a área da tubulação que sai da bomba.

Desprezando o atrito e considerando uma aceleração gravitacional de 10 m/s² , deseja-se elevar uma pessoa de 65 kg em uma cadeira de rodas de 15 kg sobre a plataforma de 20 kg.

Qual deve ser a força exercida pelo motor da bomba sobre o fluido, para que o cadeirante seja elevado com velocidade constante?

a) 20 N
b) 100 N
c) 200 N
d) 1000 N
e) 5000 N

Para mais questões, com resolução comentada, veja também: Exercícios de Hidrostática.

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.