Hidrostática

Rafael C. Asth

Professor de Matemática e Física

A Hidrostática é uma área da física que estuda os líquidos que estão em repouso. Esse ramo envolve diversos conceitos como a densidade, a pressão, o volume e a força empuxo.

Principais Conceitos da Hidrostática

Densidade

A densidade determina a concentração de matéria num determinado volume. Ela representa a relação entre a massa e o volume ocupado por esta massa.

Elementos químicos e substâncias (sólidas, líquidas e gasosas), que ocupem mesmo volume, possuem massas diferentes. É a densidade que expressa esta relação.

Corpo sólido imerso em um fluido

Se a densidade do corpo for menor que a densidade do fluido, o corpo flutuará na superfície do fluido;
$reto d com corpo subscrito menor que espaço reto d com fluido subscrito$

Gelo flutuando no copo. — A água líquida é mais densa do que na fase sólida.

Se a densidade do corpo for equivalente à densidade do fluido, o corpo ficará em equilíbrio com o fluido;
$d com c o r p o subscrito fim do subscrito igual a d com f l u i d o subscrito fim do subscrito$

Se a densidade do corpo for maior que a densidade do fluido, o corpo afundará.
$d com c o r p o subscrito fim do subscrito maior que d com f l u i d o subscrito fim do subscrito$

Gelo no copo com álcool. — A densidade do álcool é maior que a do gelo.

Fórmula da densidade

$começar estilo tamanho matemático 18px reto d espaço igual a espaço reto m sobre reto V fim do estilo$

sendo,
d: densidade
m: massa (em Kg)
v: volume (em m³)

A unidade de medida é o $k g dividido por m ³$ . Também é usualmente expressa em grama por centímetro cúbico (g/cm³) ou em grama por mililitro (g/mL).

Leia também sobre a Densidade e a Densidade da Água.

Pressão

A pressão é um conceito essencial da hidrostática, e nessa área de estudo é chamada pressão hidrostática. Ela determina a pressão que exercem os fluidos.

Como exemplo, podemos pensar na pressão que sentimos quando estamos nadando. Assim, quanto mais fundo mergulharmos, maior será a pressão hidrostática.

Esse conceito está intimamente relacionado com a densidade do fluido e a aceleração da gravidade. Sendo assim, a pressão hidrostática é calculada pela seguinte fórmula:

$começar estilo tamanho matemático 18px incremento reto P espaço igual a espaço reto d espaço. espaço incremento reto h espaço. espaço reto g fim do estilo$

Onde,
P: pressão hidrostática
d: densidade do líquido (em g/cm3)
h: altura do líquido no recipiente (em m)
g: aceleração da gravidade (em m/s²)

A unidade de medida de pressão hidrostática é o Pascal (Pa), mas também é utilizado a atmosfera (atm) e o milímetro de mercúrio (mmHg);

Obs: Note que a pressão hidrostática não depende do formato do recipiente. Ela depende da densidade do fluido, da altura da coluna do líquido e da gravidade do local.

Empuxo

O empuxo, também chamado impulsão, é uma força hidrostática que atua num corpo imerso em um fluido. Dessa forma, a força empuxo é a força resultante exercida pelo fluido sobre determinado corpo.

Como exemplo, podemos pensar no nosso corpo que parece mais leve quando estamos na água, seja na piscina ou no mar.

Observe que essa força exercida pelo líquido sobre o corpo já era estudada na Antiguidade.

O matemático grego Arquimedes foi quem realizou uma experiência hidrostática que permitia calcular o valor da força empuxo (vertical e para cima) que torna um corpo mais leve no interior de um fluido. Note que ela atua em sentido contrário à força peso.

Assim, o enunciado do Teorema de Arquimedes ou Lei do Empuxo é:

“Todo corpo mergulhado num fluido recebe um impulso de baixo para cima igual ao peso do volume do fluido deslocado, por esse motivo, os corpos mais densos que a água, afundam, enquanto os menos densos flutuam”.

Em relação à força empuxo, podemos concluir que:

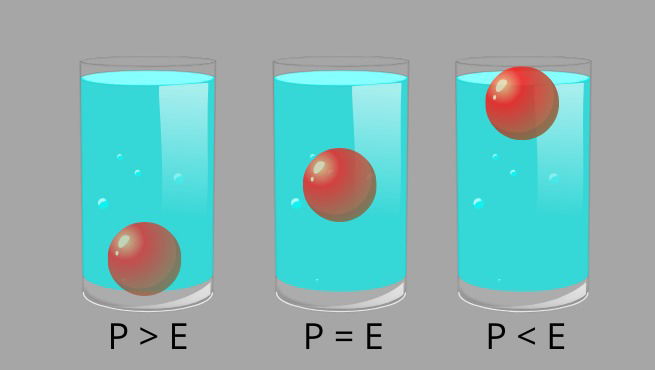
Se a força do empuxo (E) tiver maior intensidade que a força peso (P), o corpo subirá para a superfície;
Se a força empuxo (E) tiver a mesma intensidade que a força peso (P) o corpo não subirá nem descerá, permanecendo em equilíbrio;
Se a força empuxo (E) tiver menor intensidade que a força peso (P), o corpo afundará.

Lembre-se que a força empuxo é uma grandeza vetorial, ou seja, possui direção, módulo e sentido.

No Sistema Internacional (SI), o empuxo (E) é dado em Newton (N) e calculado pela seguinte fórmula:

$começar estilo tamanho matemático 18px reto E espaço igual a espaço reto d com reto f subscrito espaço. espaço reto V com fd subscrito espaço. espaço reto g fim do estilo$

Onde,

E: força empuxo (em N)
d_f: densidade do fluido (em kg/m³)
V_fd: volume do fluido deslocado (em m³)
g: aceleração da gravidade (em m/s²)

Leia a fórmula do empuxo.

Balança Hidrostática

A balança hidrostática foi inventada pelo físico, matemático e filósofo italiano Galileu Galilei (1564-1642).

Baseada no Princípio de Arquimedes, esse instrumento serve para medir a força empuxo exercida em um corpo imerso em um fluido.

Ou seja, ela determina o peso de um objeto imerso em um líquido, que por sua vez é mais leve que no ar.

Balança Hidrostática

Lei Fundamental da Hidrostática

O Teorema de Stevin é conhecido como a “Lei fundamental da Hidrostática”. Essa teoria postula a relação de variação entre os volumes dos líquidos e da pressão hidrostática. Seu enunciado é expresso da seguinte maneira:

“A diferença entre as pressões de dois pontos de um fluido em equilíbrio (repouso) é igual ao produto entre a densidade do fluido, a aceleração da gravidade e a diferença entre as profundidades dos pontos.”

O Teorema de Stevin é representado pela seguinte fórmula:

$começar estilo tamanho matemático 18px incremento reto P espaço igual a espaço reto d. espaço reto g. espaço incremento reto h fim do estilo$

$começar estilo tamanho matemático 18px incremento reto P espaço igual a espaço reto gama espaço vezes espaço incremento reto h fim do estilo$

Onde,

∆P: variação da pressão hidrostática
γ: peso específico do fluido
∆h: variação da altura da coluna de líquido
d: densidade
g: aceleração da gravidade

No Sistema Internacional (SI):

a variação da pressão hidrostática é em Pascal (Pa);
o peso específico do fluido é em Newton por metros cúbicos (N/m³);
a variação da altura da coluna do líquido é em metros (m);
a densidade é em quilograma por metros cúbicos (Kg/m³);
a aceleração da gravidade é em metros por segundo ao quadrado (m/s²).

Hidrostática e Hidrodinâmica

Enquanto a hidrostática estudo os líquidos em repouso, a hidrodinâmica é o ramo da física que estuda o movimento desses fluidos.

Exercícios de hidrostática com Gabarito

Exercício 1

(PUC-PR) O empuxo é um fenômeno bastante familiar. Um exemplo é a facilidade relativa com que você pode se levantar de dentro de uma piscina em comparação com tentar se levantar de fora da água, ou seja, no ar.

De acordo com o princípio de Arquimedes, que define empuxo, marque a proposição correta:

a) Quando um corpo flutua na água, o empuxo recebido pelo corpo é menor que o peso do corpo.
b) O princípio de Arquimedes somente é válido para corpos mergulhados em líquidos e não pode ser aplicado para gases.
c) Um corpo total ou parcialmente imerso em um fluido sofre uma força vertical para cima e igual em módulo ao peso do fluido deslocado.
d) Se um corpo afunda na água com velocidade constante, o empuxo sobre ele é nulo.
e) Dois objetos de mesmo volume, quando imersos em líquidos de densidades diferentes, sofrem empuxos iguais.

Ver Resposta

Alternativa c

a) ERRADA. Para flutuar a força vertical para cima (empuxo) deve ser maior que a força vertical para baixo (peso).

b) ERRADA. O Princípio de Arquimedes se aplica aos fluidos, o que inclui os gases.

d) ERRADA. Um corpo imerso em um fluido está sempre sob efeito do empuxo, não importando se está ou não em movimento.

e) ERRADA. A força empuxo é diretamente proporcional a densidade do fluido. Maior densidade, maior empuxo.

Exercício 2

(UERJ-RJ) Uma balsa, cuja forma é um paralelepípedo retângulo, flutua em um lago de água doce. A base de seu casco, cujas dimensões são iguais a 20 m de comprimento e 5 m de largura, está paralela à superfície livre da água e submersa a uma distância do dessa superfície. Admita que a balsa é carregada com 10 automóveis, cada um pesando 1.200 kg, de modo que a base do casco permaneça paralela à superfície livre da água, mas submersa a uma distância d dessa superfície.

Se a densidade da água é 1,0 × 10³ kg/m³, a variação (d – do), em centímetros, é de: (g=10m/s²)

a) 2
b) 6
c) 12
d) 24
e) 22

Ver Resposta

Resposta correta: alternativa c

Para a balsa flutuar a força peso deve ser igual a força empuxo, havendo um equilíbrio.

E = P

Força peso

$P espaço igual a espaço m g$

A massa é:

m = 10 . 1 200 = 12 000 kg

Substituindo os valores na fórmula:

$P espaço igual a espaço 12 espaço 000 espaço. espaço 10 espaço igual a espaço 120 espaço 000 espaço N$

Volume do fluído deslocado pela balsa

$V com f d subscrito fim do subscrito igual a 20 espaço. espaço 5 espaço. espaço parêntese esquerdo d espaço menos espaço d com 0 subscrito parêntese direito espaço V com f d subscrito fim do subscrito igual a 100 espaço. espaço parêntese esquerdo d espaço menos espaço d com 0 subscrito parêntese direito espaço$

Onde d - d0 é a altura entre o casco e a superfície.

Força empuxo

$E espaço igual a espaço V com f d subscrito fim do subscrito espaço. espaço d com f subscrito espaço. espaço g$

Substituindo os valores:

$E espaço igual a espaço 100 espaço. espaço parêntese esquerdo d espaço menos espaço d com 0 subscrito parêntese direito espaço. espaço 10 ao cubo espaço. espaço 10 E espaço igual a espaço 100 espaço. espaço 1000 espaço. espaço 10 espaço. espaço parêntese esquerdo d espaço menos espaço d com 0 subscrito parêntese direito E espaço igual a espaço 1 espaço 000 espaço 000 espaço. espaço parêntese esquerdo d espaço menos espaço d com 0 subscrito parêntese direito$

Igualando E com P e resolvendo para d - d0

$E espaço igual a espaço P 1 espaço 000 espaço 000 espaço parêntese esquerdo d espaço menos espaço d com 0 subscrito parêntese direito espaço igual a espaço 120 espaço 000 d espaço menos espaço d com 0 subscrito igual a numerador 120 espaço 000 sobre denominador 1 espaço 000 espaço 000 fim da fração igual a 0 vírgula 12$

Como as unidades estão no SI a resposta está em metros. Portanto:

d - d0 = 0,12 m ou 12 cm.

Exercício 3

(UNIFOR-CE) Dois líquidos, A e B, quimicamente inertes, e não-miscíveis entre si, de densidades dA=2,80g/cm³ e dB=1,60g/cm³, respectivamente, são colocados em um mesmo recipiente. Sabendo que o volume do líquido A é o dobro do de B, a densidade da mistura, em g/cm³, vale:

a) 2,40
b) 2,30
c) 2,20
d) 2,10
e) 2,00

Ver Resposta

Resposta correta: a) 2,40

A densidade do fluido é a massa total do fluido dividido pelo volume total do fluido.

$d com f subscrito igual a m com f subscrito sobre V com f subscrito igual a numerador m com a subscrito mais m com b subscrito sobre denominador V com a subscrito mais V com b subscrito fim da fração$

Temos que o volume de A é igual ao dobro do volume de B.

$V com a subscrito igual a 2 espaço. espaço V com b subscrito$

Substituindo na equação da densidade do fluido:

$d com f subscrito igual a numerador m com a subscrito mais m com b subscrito sobre denominador V com a subscrito mais V com b subscrito fim da fração d com f subscrito igual a numerador m com a subscrito mais m com b subscrito sobre denominador 2 espaço V com b subscrito mais V com b subscrito fim da fração d com f subscrito igual a numerador m com a subscrito mais m com b subscrito sobre denominador 3 V com b subscrito fim da fração$

Determinando as massas dos fluidos.

Massa de A

$m com a subscrito sobre V com a subscrito igual a d com a subscrito m com a subscrito igual a d com a subscrito. V com a subscrito m com a subscrito igual a 2 vírgula 80. V com a subscrito$

Como o volume de A é o dobro do volume de B, vamos substituir A = 2B.

$m com a subscrito igual a d com a subscrito. V com a subscrito espaço m com a subscrito igual a espaço d com a subscrito espaço. espaço 2 V com b subscrito m com a subscrito igual a 2 vírgula 80 espaço. espaço 2 V com b subscrito igual a 5 vírgula 60 V com b subscrito$

Massa de B

$m com b subscrito sobre V com b subscrito igual a b com a subscrito m com b subscrito igual a d com b subscrito. V com b subscrito m com b subscrito igual a 1 vírgula 60. V com b subscrito$

Substituindo as massas de A e B na equação da densidade

$d com f subscrito igual a numerador m com a subscrito mais m com b subscrito sobre denominador 3 V com b subscrito fim da fração d com f subscrito igual a numerador 5 vírgula 60 V com b subscrito mais 1 vírgula 60 V com b subscrito sobre denominador 3 V com b subscrito fim da fração d com f subscrito espaço igual a espaço numerador 7 vírgula 20 V com b subscrito sobre denominador 3 V com b subscrito fim da fração d com f subscrito espaço igual a espaço numerador 7 vírgula 20 riscado diagonal para cima sobre V com b subscrito fim do riscado sobre denominador 3 riscado diagonal para cima sobre V com b subscrito fim do riscado fim da fração igual a numerador 7 vírgula 20 sobre denominador 3 fim da fração igual a 2 vírgula 40$

Portanto, a densidade do fluido é 2,40 g/cm³.

Para mais questões, com resolução comentada, veja também: Exercícios de Hidrostática.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações