Fórmula do empuxo

Rafael C. Asth
Rafael C. Asth
Professor de Matemática e Física

Empuxo é a força exercida pelos fluidos em corpos submersos, total ou parcialmente. Também conhecido como teorema de Arquimedes.

A pressão do fluido sobre o corpo produz uma força resultante com a direção do peso, mas com o sentido contrário, de baixo para cima.

A fórmula para calcular o empuxo, é:

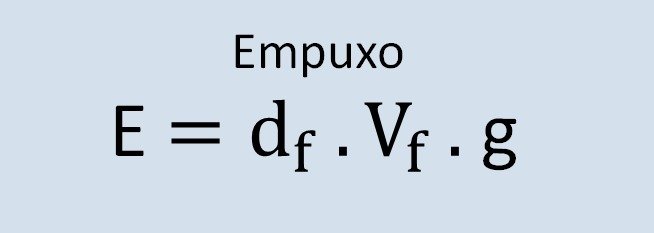
Onde:

E, é o módulo do empuxo, medido em Newtons (N);

df é a densidade do fluido, medida em kg / m³;

Vf é o volume do fluido deslocado, medido em m³;

g, é a aceleração da gravidade, medida em m/s².

A intensidade do empuxo é igual a do peso do volume de fluido deslocado, e age no centro de gravidade desse volume.

O empuxo é o produto entre três valores: densidade do fluido, volume de fluido deslocado e aceleração da gravidade.

A densidade é uma característica própria do fluido. Existem tabelas que oferecem valores de densidade para vários fluidos.

Para água a 4 °C, a densidade é 1 g / cm³ ou 1 000 kg / m³.
Para o ar, a 20 °C e pressão de 1 atmosfera, a densidade é de 0,0012 g / cm³ ou 1,2 kg / m³.

O volume de fluido deslocado depende da geometria do corpo, e se ele está total ou parcialmente submerso. Quanto maior o volume do corpo, mais líquido ele descola, logo, maior será o empuxo.

A aceleração da gravidade é de, aproximadamente, 9,81 m/s².

Exemplo:
Um corpo tem a forma de um paralelepípedo com volume de 2 m³ e foi totalmente imerso em um líquido com densidade de 900 kg / m³. Considerando a aceleração da gravidade igual a 9,81 m / s², calcule a intensidade da força empuxo que age sobre o corpo.

Dados:
Vf = 2 m³;
df = 900 kg/m³
g = 9,81 m/s²

Aplicando a fórmula do empuxo

E = df . Vf . g
E = 900 . 2 . 9,8
E = 17 640 N

A fórmula do empuxo

Se o módulo do empuxo (E), é igual ao do peso de fluido deslocado (Pf), temos:

E = Pf (equação 1)

O peso é igual ao produto entre massa e aceleração da gravidade, Pf = mf . g. Substituindo em 1:

E = mf . g (equação 2)

Na relação da densidade, df = mf / Vf, podemos isolar a massa do fluido e dizer ser igual à densidade do fluido, multiplicado pelo volume de fluido deslocado.

mf = df . Vf

Substituindo na equação 2, temos a equação do empuxo:

E = df . Vf . g

Aprenda mais sobre o teorema de Arquimedes.

Exercício 1

Um corpo que possui um peso de 200 N, foi imerso em água. Verificou-se que, uma vez submerso, seu peso era de 120 N. Com base nestas informações e, considerando a densidade da água igual 1 000 kg/m³ e a aceleração da gravidades igual a 9,8 m/s², calcule:

a) O empuxo recebido pelo corpo.
b) O volume do corpo.

a) O empuxo será igual a diferença entre seu peso fora da água e seu peso dentro da água.

Empuxo = Peso fora da água - Peso dentro da água (peso aparente)

Empuxo = 200 N - 120 N = 80 N.

b) O volume do corpo.

O volume do corpo é igual ao volume de fluido deslocado.

Usando a fórmula para o empuxo:

E = Vf . df . g

Isolando Vf e substituindo os valores conhecidos:

V com f espaço igual a espaço subscrito fim do subscrito numerador E sobre denominador d f espaço. espaço g fim da fração espaço igual a espaço numerador 80 espaço N sobre denominador 1000 espaço. espaço 9 vírgula 81 espaço fim da fração espaço aproximadamente igual espaço 0 vírgula 00815 espaço m ³ espaço aproximadamente igual espaço 8 vírgula 15 espaço x espaço 10 à potência de menos 3 fim do exponencial espaço m ao cubo

Exercício 2

(Fuvest - SP). Um tijolo tem massa igual a 2 kg e volume igual a 1 000 cm³.

a) Determine a densidade do tijolo.
b) Calcule o peso aparente do tijolo quando totalmente imerso em água.

Dados: g = 10 m/s² e densidade da água = 1,0 g / cm³

a) Determine a densidade do tijolo.

Em g / cm³

2 kg = 2 000 g

d com t i j o l o subscrito fim do subscrito espaço igual a espaço numerador m a s s a sobre denominador v o l u m e fim da fração espaço igual a espaço numerador 2 espaço 000 espaço g sobre denominador 1 espaço 000 espaço c m ao cubo fim da fração espaço igual a espaço 2 espaço g dividido por c m ³

Em kg / m³

Passando o volume do tijolo de cm³ para m³
1000 cm³ = 0,001 m³

Calculando a densidade

d com t i j o l o subscrito fim do subscrito igual a numerador m a s s a sobre denominador v o l u m e fim da fração espaço igual a espaço numerador 2 espaço k g sobre denominador 0 vírgula 001 espaço m ³ fim da fração espaço igual a espaço 2 espaço 000 espaço k g espaço dividido por espaço m ³

b) Calcule o peso aparente do tijolo quando totalmente imerso em água.

O peso aparente é a diferença entre o peso real e o empuxo.

Peso aparente = peso real - empuxo

Calculando o empuxo
E = df . Vf . g
E = 1,0 . 0,001 . 10 = 0,01 N

Calculando o peso real
P = m . g
P = 2 kg . 10 m/s²
P = 20 m/s²

Agora, podemos calcular o peso aparente

Peso aparente = peso real - empuxo
Peso aparente = 20 - 10 = 10 N

Portanto, o peso aparente é de 10 N.

Exercício 3

(Enem 2010). Durante uma obra em um clube, um grupo de trabalhadores teve de remover uma escultura de ferro maciço colocada no fundo de uma piscina vazia. Cinco trabalhadores amarraram cordas à escultura e tentaram puxá-la para cima, sem sucesso.

Se a piscina for preenchida com água, ficará mais fácil para os trabalhadores removerem a escultura, pois a

a) escultura flutuará, desta forma, os homens não precisarão fazer força para remover a escultura do fundo.

b) escultura ficará como peso menor. Desta forma, a intensidade da força necessária para elevar a escultura será menor.

c) água exercerá uma força na escultura proporcional a sua massa, e para cima. Esta força se somará à força que os trabalhadores fazem para anular a ação da força peso da escultura.

d) água exercerá uma força na escultura para baixo, e esta passará a receber uma força ascendente do piso da piscina. Esta força ajudará a anular a ação da força peso na escultura.

e) água exercerá uma força na escultura proporcional ao seu volume, e para cima. Esta força se somará à força que os trabalhadores fazem, podendo resultar em uma força ascendente maior que o peso da escultura.

Resposta correta: e) água exercerá uma força na escultura proporcional ao seu volume, e para cima. Esta força se somará à força que os trabalhadores fazem, podendo resultar em uma força ascendente maior que o peso da escultura.

Explicação

Um fluido exerce uma força ascendente (de baixo para cima) em corpos submersos, chamada empuxo. A intensidade desta força é proporcional ao peso do fluido deslocado.

Essa quantidade de fluido deslocado é igual ao volume do corpo que foi imerso. Essa força é, portanto, proporcional ao volume do corpo, pois, quanto maior o volume, maior a quantidade de fluido deslocado.

É possível que esta força somada a força que os trabalhadores exercem, seja maior que o peso da estátua.

Estude com exercícios de:
Densidade
Hidrostática

Você pode se interessar por:

Hidrostática
Fórmulas de física
Pressão hidrostática
Princípio de Pascal
Teorema de Stevin

Rafael C. Asth
Rafael C. Asth
Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.
Veja também