Ábaco: entenda o que é e como funciona (aprenda a usar)
O ábaco, do grego άβακας, é um instrumento de cálculo utilizado há milênios para realizar as operações matemáticas básicas de adição, subtração, multiplicação e divisão.
Possui uma estrutura com hastes que representam as ordens e contas deslizantes para os algarismos. Foi amplamente utilizado por civilizações antigas, como os chineses, japoneses, romanos, gregos e babilônios, e até hoje é empregado como ferramenta didática de Matemática no ensino fundamental dos anos iniciais (1º ao 5º).
Neste conteúdo você encontra:
- Entendendo a estrutura do ábaco
- Como ler números no ábaco
- Realizando cálculos no ábaco
- História do ábaco
Entendendo a estrutura do ábaco
Há diversos tipos de ábacos, porém os mais comuns são:
Ábaco simples: utilizado para ensinar os primeiros conceitos de contagem e operações matemáticas básicas. Conhecido como ábaco escolar.
Soroban japonês: possui uma estrutura mais sofisticada, permitindo operações avançadas, como multiplicação e divisão.

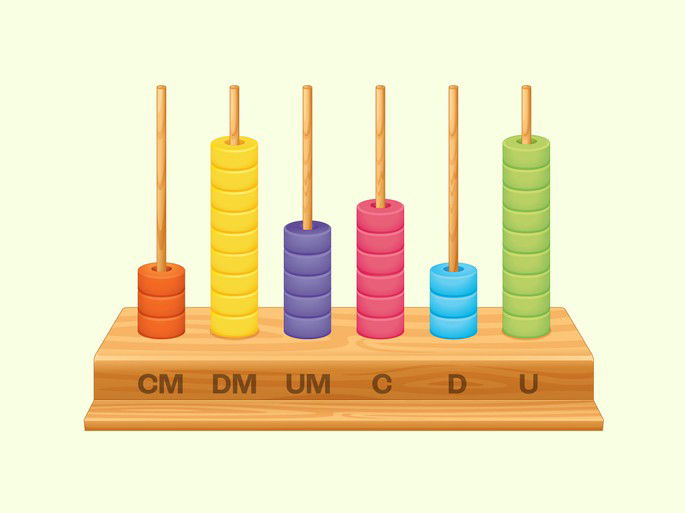
Em geral, um ábaco é composto por hastes verticais e contas que representam unidades, dezenas, centenas e assim por diante. Cada coluna equivale a uma posição do sistema decimal.
Como ler números no ábaco
Para interpretar um número no ábaco:
- Cada haste representa uma ordem numérica (unidade, dezena, centena, etc.).
- As contas deslizam para indicar quantidades. Se um ábaco tem uma haste com cinco contas e três estão levantadas, significa que há um "3" nessa posição. No caso do ábaco escolar como discos são livres pode-se colocar apenas a quantidade de discos necessárias em cada ordem para representar um número.
- O número final é lido da esquerda para a direita, de acordo com as contas levantadas em cada haste ou a quantidade de contas em cada uma delas.
Exemplo: observe a figura abaixo.

Se a haste que representa as unidades (U) tem oito contas, a das dezenas (D) tem cinco, a das centenas (C) tem sete e das unidades de milhar (UM) tem três isso significa que escrevemos o número 3758.
Realizando cálculos no ábaco
Como fazer contas de somar (adição) usando o ábaco
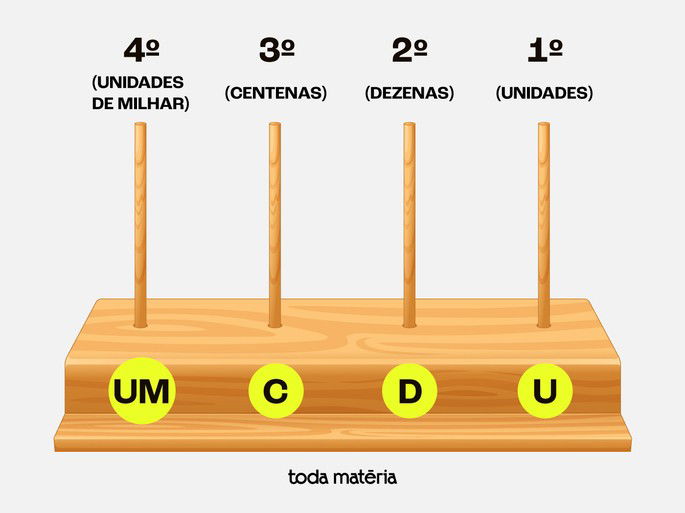
Vamos utilizar como exemplo um ábaco do tipo escolar com 4 hastes e cada uma delas representa uma ordem numérica e só podem ser colocadas em cada haste no máximo 9 discos (contas):
Unidades (U) – Primeira haste à direita
Dezenas (D) – Segunda haste
Centenas (C) – Terceira haste
Unidades de Milhar (UM) – Quarta haste
Agora, vamos ver alguns exemplos passo a passo:
Exemplo 1: 23 + 15
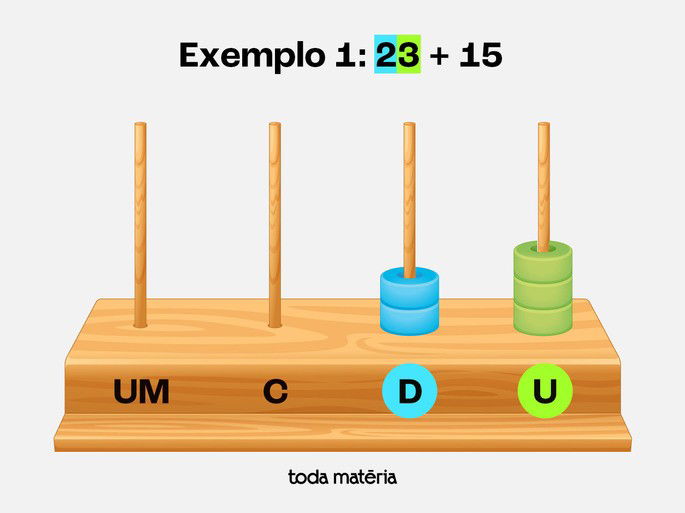
Passo 1: Representar o número 23 no ábaco
Coloque 3 contas na haste das unidades
Coloque 2 contas na haste das dezenas
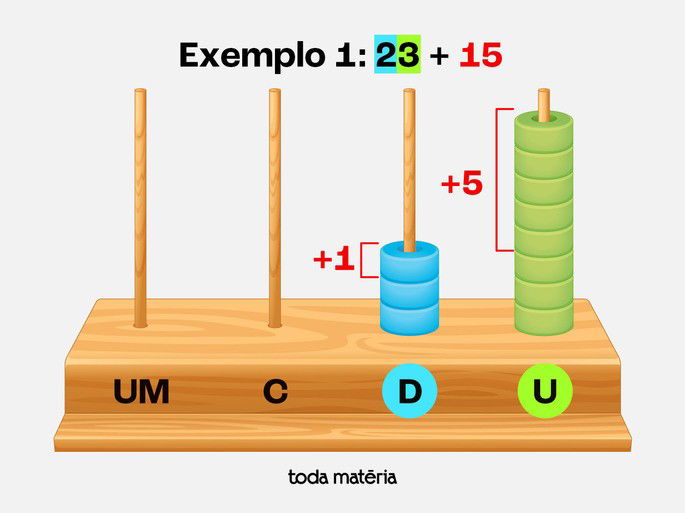
Passo 2: Adicionar o número 15
Adicione 5 contas na haste das unidades
Adicione 1 conta na haste das dezenas
Passo 3: Contar as contas em cada haste
Na haste das unidades: 3 + 5 = 8 (fica tudo na mesma haste)
Na haste das dezenas: 2 + 1 = 3
Resultado: 23 + 15 = 38
Exemplo 2: 48 + 36 (Com reagrupamento)
Passo 1: Representar o número 48 no ábaco
8 contas na haste das unidades
4 contas na haste das dezenas
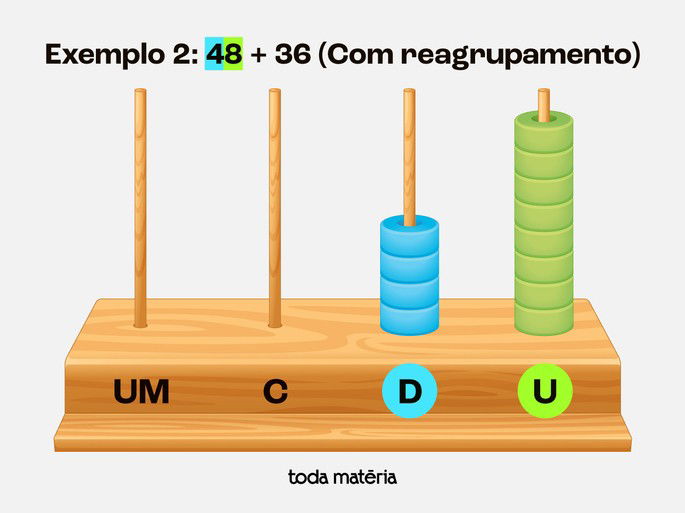
Passo 2: Adicionar o número 36
Adicione 6 contas na haste das unidades
Adicione 3 contas na haste das dezenas
Neste caso não conseguiremos colocar 14 = 8 + 6 contas na haste da unidade, então devemos separar dez (10 unidades = 1 dezena) delas e acrescentar uma conta a mais na haste da dezena e as 4 restantes permanecem na haste das unidades.
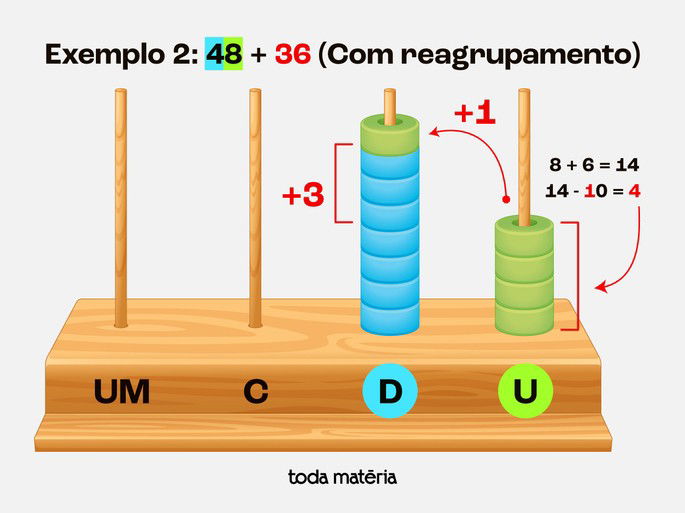
Passo 3: Contar as contas e verificar o resultado
Unidades: Deixamos 4 unidades e passamos 1 dezena para a haste das dezenas
Dezenas: 4 + 3 + 1 (a que veio do transporte) = 8
Resultado: 48 + 36 = 84
Exemplo 3: 275 + 469 (Com reagrupamento em várias ordens)
Passo 1: Representar o número 275
5 contas na haste das unidades
7 contas na haste das dezenas
2 contas na haste das centenas
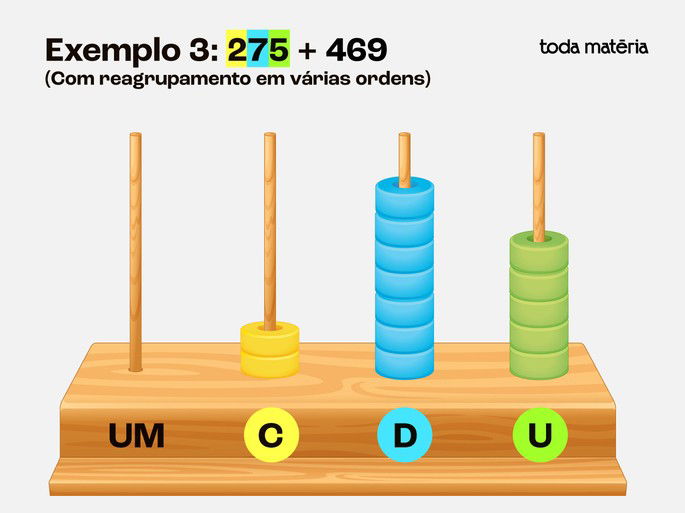
Passo 2: Adicionar o número 469
Adicione 9 contas na haste das unidades
Adicione 6 contas na haste das dezenas
Adicione 4 contas na haste das centenas
Passo 3: Contar as contas e reorganizar
Unidades: 5 + 9 = 14
Mantemos 4 unidades e passamos 1 dezena para a haste das dezenas.
Dezenas: 7 + 6 + 1 = 14
Mantemos 4 dezenas e passamos 1 centena para a haste das centenas.
Centenas: 2 + 4 + 1 = 7
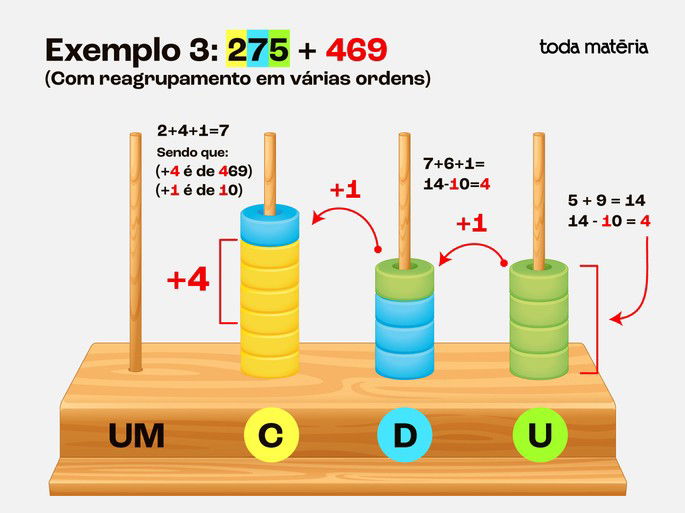
Resultado: 275 + 469 = 744
A partir desses exemplos podemos perceber como o ábaco ajuda a visualizar a adição, especialmente o conceito de reagrupamento (vai-um). Isso torna o aprendizado mais concreto e intuitivo.
Como fazer contas de diminuir (subtração) usando o ábaco
A subtração no ábaco é feita removendo contas das hastes, representando a diminuição de valores. Assim como na adição, cada haste do ábaco representa uma ordem numérica:
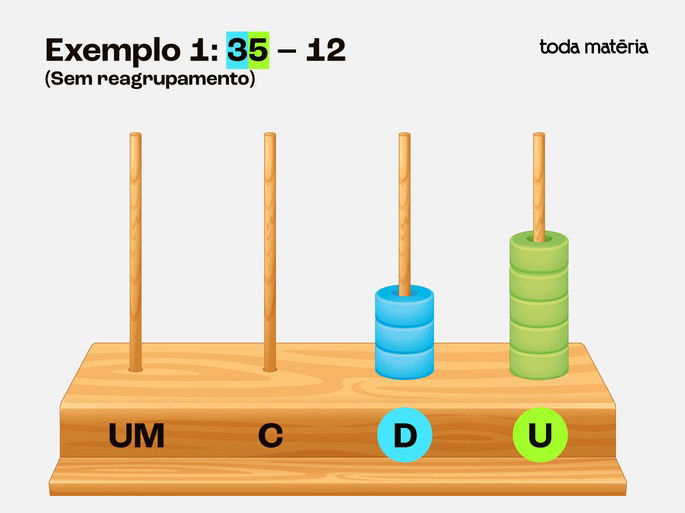
Exemplo 1: 35 – 12 (Sem reagrupamento)
Passo 1: Representar o número 35 no ábaco
Coloque 5 contas na haste das unidades
Coloque 3 contas na haste das dezenas
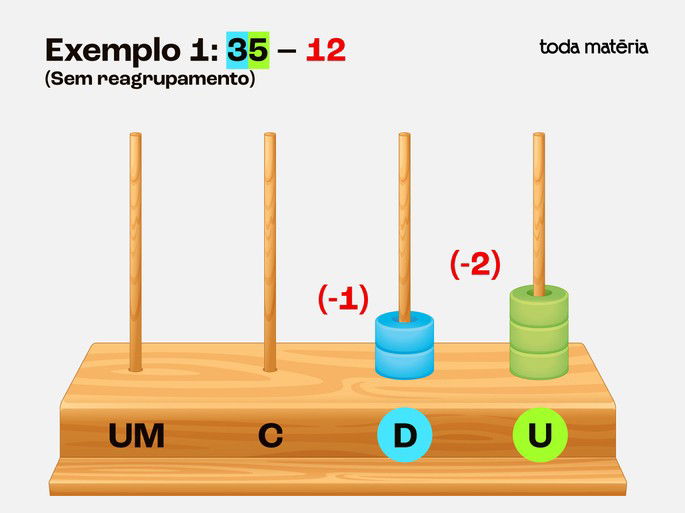
Passo 2: Remover 12 do ábaco
Remova 2 contas da haste das unidades
Remova 1 conta da haste das dezenas
Passo 3: Contar as contas restantes
Unidades: 5 - 2 = 3
Dezenas: 3 - 1 = 2
Resultado: 35 - 12 = 23
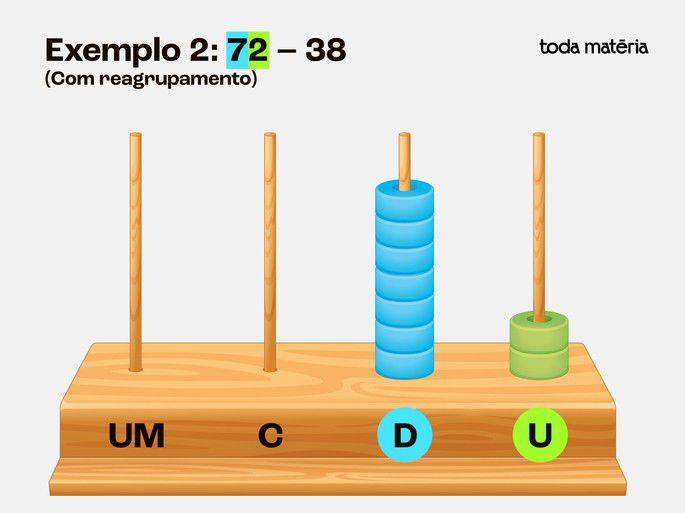
Exemplo 2: 72 – 38 (Com reagrupamento)
Passo 1: Representar o número 72 no ábaco
Coloque 2 contas na haste das unidades
Coloque 7 contas na haste das dezenas
Passo 2: Remover 38 do ábaco
Precisamos remover 8 unidades, mas só temos 2.
Reagrupamento: Pegamos 1 dezena (deixando 6 dezenas) e trocamos por 10 unidades. Agora temos 12 unidades.
Remova 8 contas das unidades → Sobram 4.
Remova 3 contas das dezenas → Sobram 3.
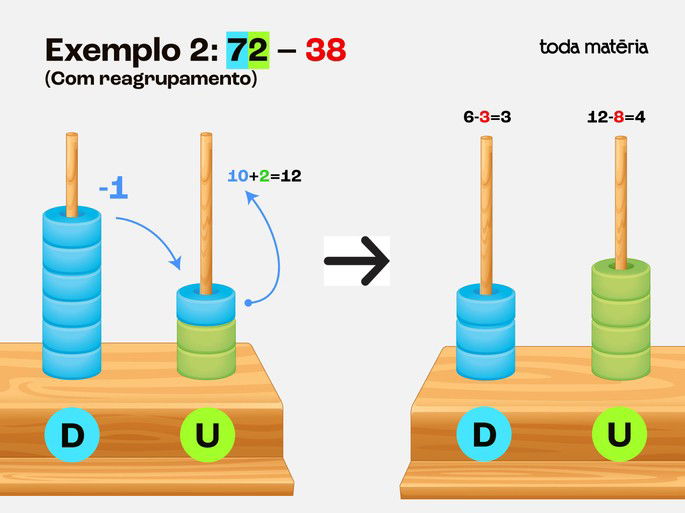
Passo 3: Contar as contas restantes
Unidades: 4
Dezenas: 3
Resultado: 72 - 38 = 34
Exemplo 3: 503 – 267 (Com reagrupamento em várias ordens)
Passo 1: Representar o número 503 no ábaco
3 contas na haste das unidades
0 contas na haste das dezenas
5 contas na haste das centenas
Passo 2: Remover 267 do ábaco
Unidades: Precisamos remover 7, mas só temos 3.
Pegamos 1 centena e trocamos por 10 dezenas.
Depois pegamos 1 dezena e trocamos por 10 unidades.
Agora temos 13 unidades.
Removemos 7, sobrando 6.
Dezenas: Precisamos remover 6, mas temos 9 (porque trocamos antes).
Removemos 6, sobrando 3.
Centenas: Precisamos remover 2, sobrando 2.
Passo 3: Contar as contas restantes
Unidades: 6
Dezenas: 3
Centenas: 2
Resultado: 503 - 267 = 236
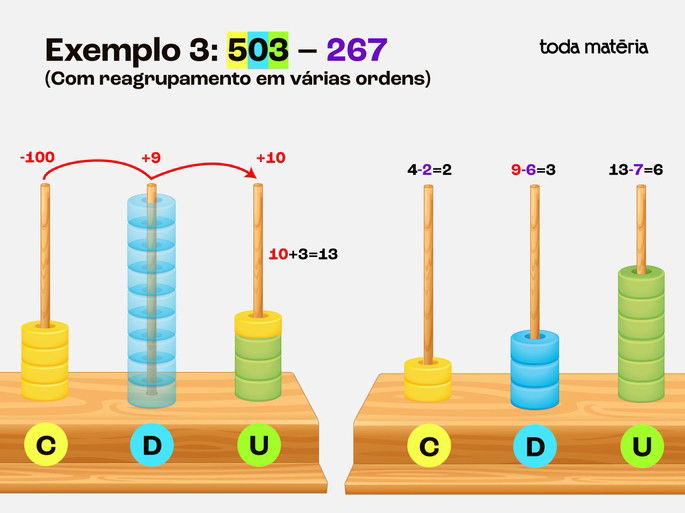
Esses exemplos mostram como o ábaco facilita a compreensão da subtração, especialmente o conceito de reagrupamento (pegar emprestado). Isso auxilia os alunos a entenderem melhor o processo de subtração de forma prática.
Como fazer contas de multiplicação usando o ábaco
Como a multiplicação é uma adição de parcelas iguais, basta aplicarmos este conceito no ábaco.
Vejamos alguns exemplos detalhadamente.
Exemplo 1: 3 × 2 (Multiplicação simples, sem reagrupamento)
Queremos calcular 3 vezes 2, o que significa 2 + 2 + 2.
Passo 1: Configurar o primeiro grupo:
Coloque 2 contas na haste das unidades.
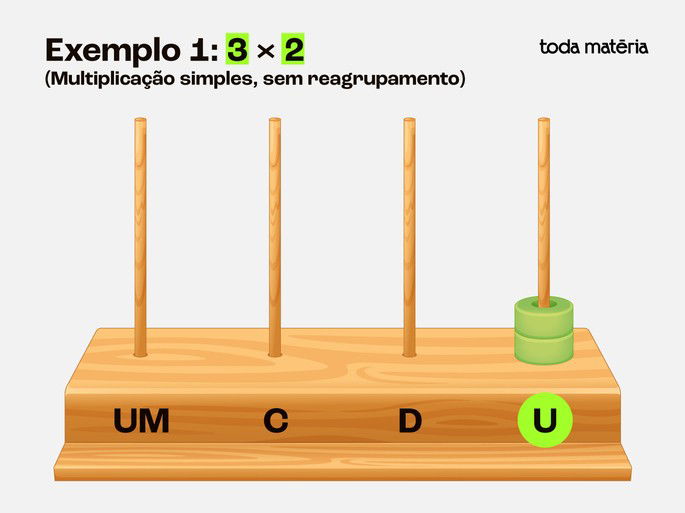
Passo 2: Repetir a adição mais duas vezes:
Adicione mais 2 contas (agora temos 4),
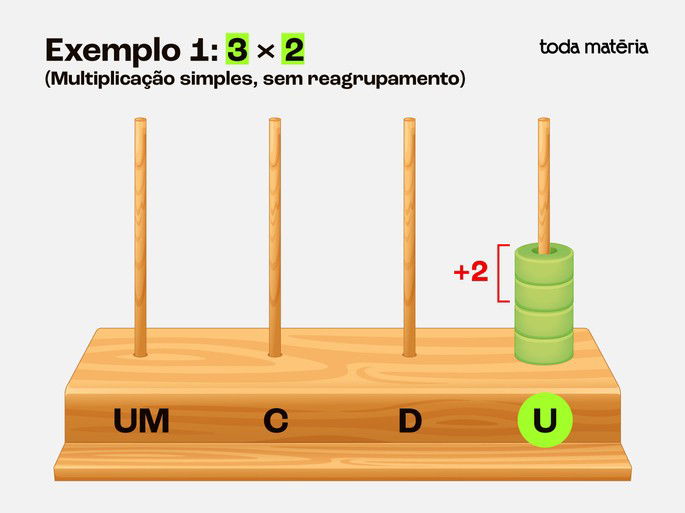
E em seguida adicionar mais 2 contas (agora temos 6).
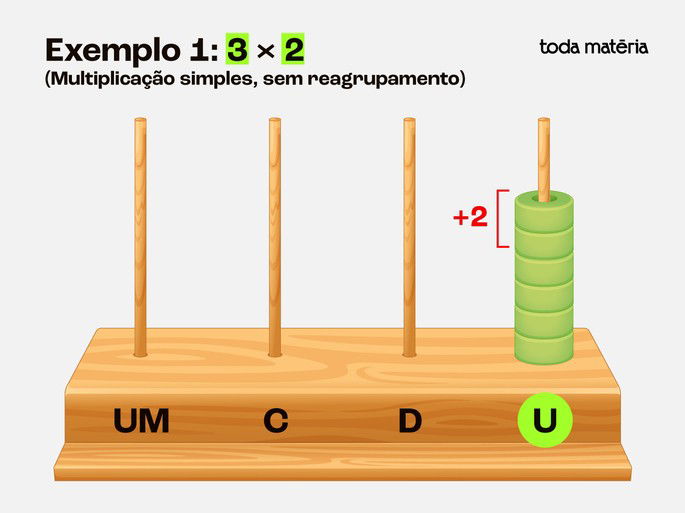
Passo 3: Ler o resultado:
O total de contas na haste das unidades é 6.
Resposta: 3 × 2 = 6
Exemplo 2: 6 × 7 (Multiplicação com reagrupamento)
Agora, vamos calcular 6 vezes 7. Como 6 × 7 = 42, precisaremos reagrupar.
Passo 1: Colocar o primeiro grupo de 7 contas:
Adicione 7 contas na haste das unidades.
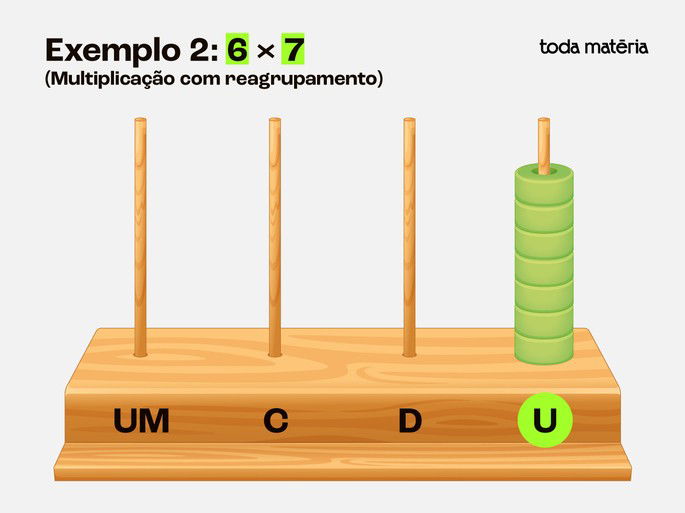
Passo 2: Repetir a adição mais cinco vezes:
Agora temos 14 (7+7), depois 21, depois 28, depois 35, e finalmente 42.
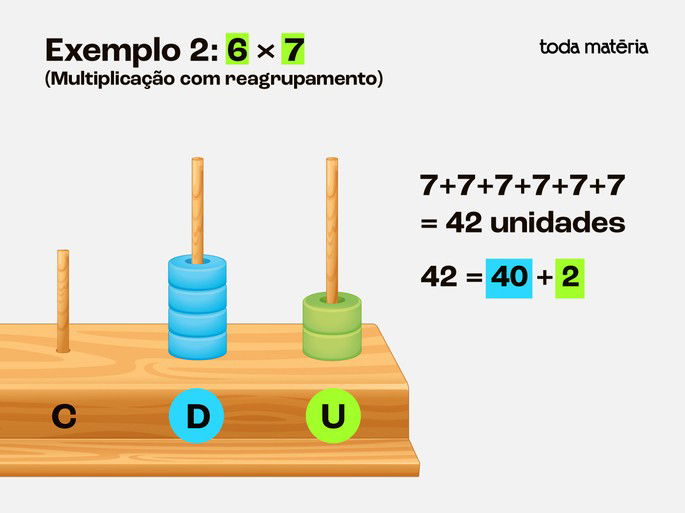
Passo 3: Reagrupar:
Como 42 tem 4 dezenas e 2 unidades, deixamos 2 contas na haste das unidades e passamos 4 contas para a haste das dezenas.
Passo 4: Ler o resultado:
Temos 4 contas na haste das dezenas e 2 contas na haste das unidades, formando 42.
Resposta: 6 × 7 = 42
Exemplo 3: 25 × 3 (Multiplicação com dezenas e unidades)
Passo 1: Queremos calcular 25 vezes 3. Podemos decompor esse número em partes:
25 = 20 + 5, então calculamos separadamente (20 × 3) + (5 × 3).
Passo 2: Multiplicar 20 por 3: Colocamos 2 contas na haste das dezenas (20).
Repetimos esse valor 3 vezes, resultando em 6 contas na haste das dezenas (60).
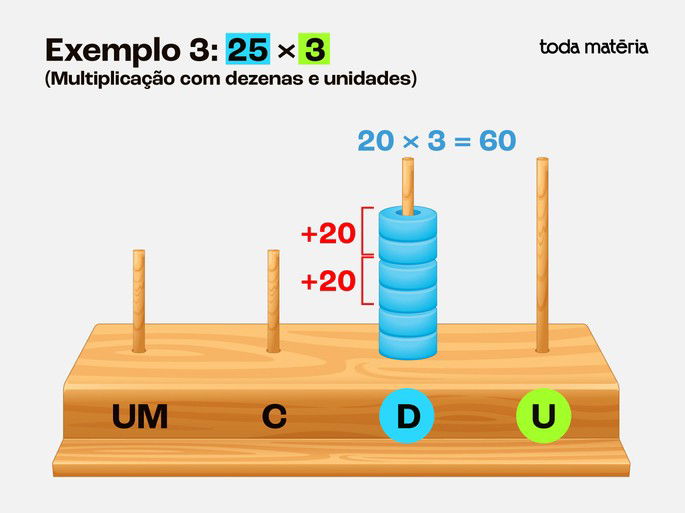
Passo 3: Multiplicar 5 por 3: Colocamos 5 contas na haste das unidades.
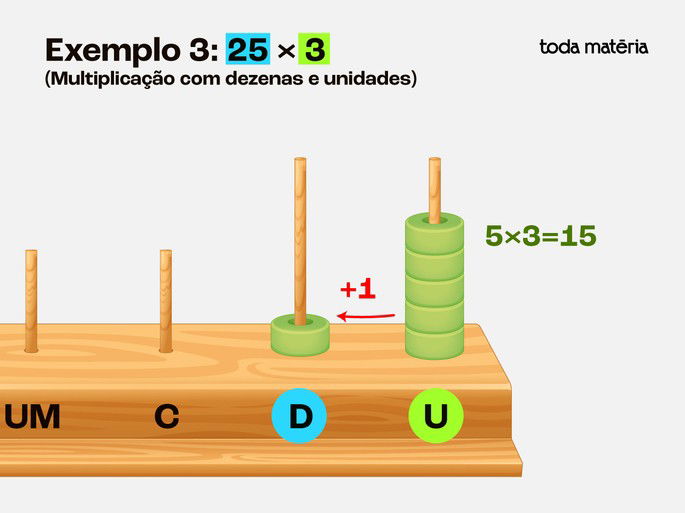
Repetimos esse valor 3 vezes, resultando em 15 contas.
Passo 4: Reagrupar:
Como 15 tem 1 dezena e 5 unidades, deixamos 5 na haste das unidades e movemos 1 conta para a haste das dezenas.
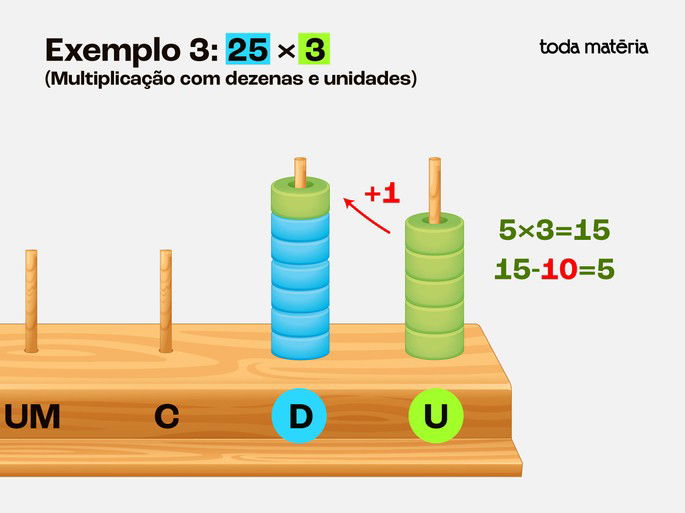
Passo 5: Ler o resultado:
Temos 7 dezenas e 5 unidades, formando 75.
Resposta: 25 × 3 = 75
A multiplicação no ábaco é feita como uma soma repetida, e quando os valores passam de 9, fazemos reagrupamentos para manter a organização. Essa abordagem ajuda os alunos a visualizar como a multiplicação funciona, facilitando a compreensão dos cálculos matemáticos.
Como fazer contas de divisão usando o ábaco
Nas operações básicas vemos que as operações aparecem de forma oposta uma da outra, assim como a multiplicação é uma soma de parcelas iguais, a divisão será uma subtração de parcelas iguais que chamamos de grupos.
Vejamos alguns exemplos passo a passo:
Exemplo 1: 96 ÷ 3 (Exata)
Passo 1: Coloque 9 dezenas e 6 unidades no ábaco.
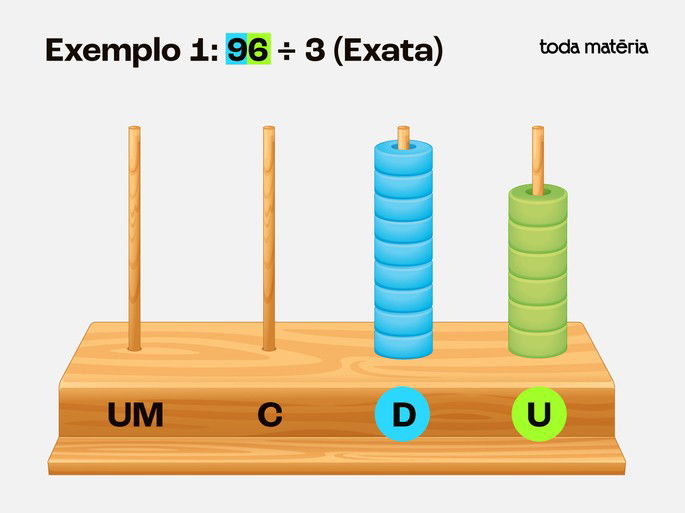
Passo 2: Repare que agora começamos da maior ordem, isto é, da esquerda para a direita. Divida as 9 dezenas em 3 grupos - Cada grupo recebe 3 dezenas.
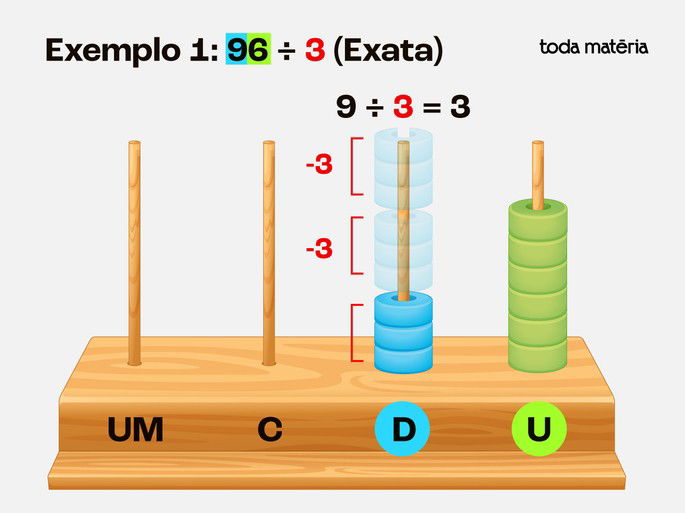
Passo 3: Divida as 6 unidades em 3 grupos - Cada grupo recebe 2 unidades.
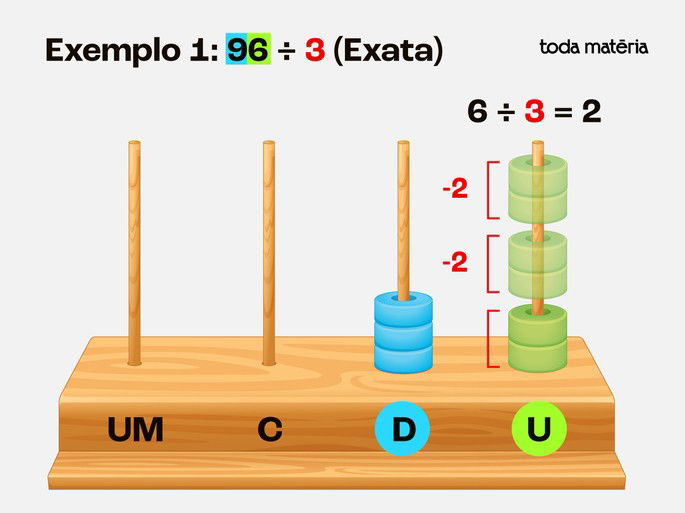
Passo 4: Ler o resultado resultado: 32 (sem resto).
Exemplo 2: 125 ÷ 5 (Exata)
Passo 1: Coloque 1 centena, 2 dezenas e 5 unidades no ábaco.
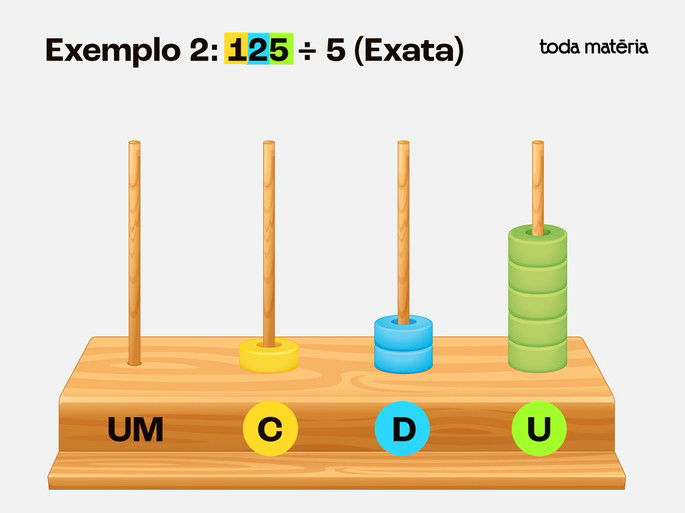
Passo 2: Troque 1 centena por 10 dezenas, ficando com 12 dezenas.
Divida 12 dezenas em 5 grupos - Cada grupo recebe 2 dezenas, restam 2 dezenas.
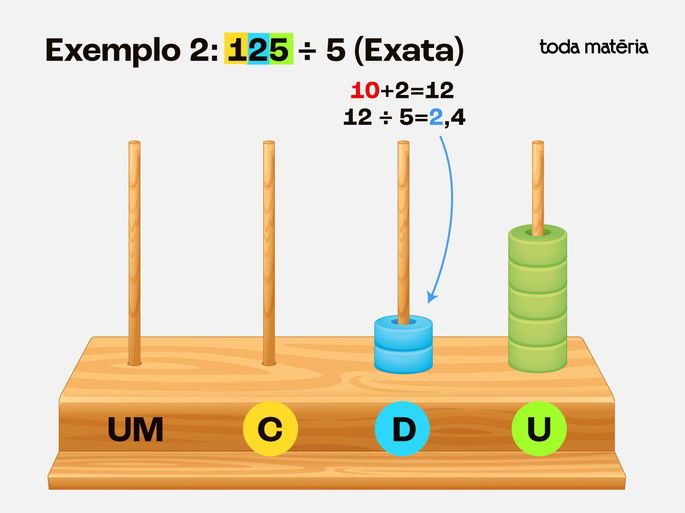
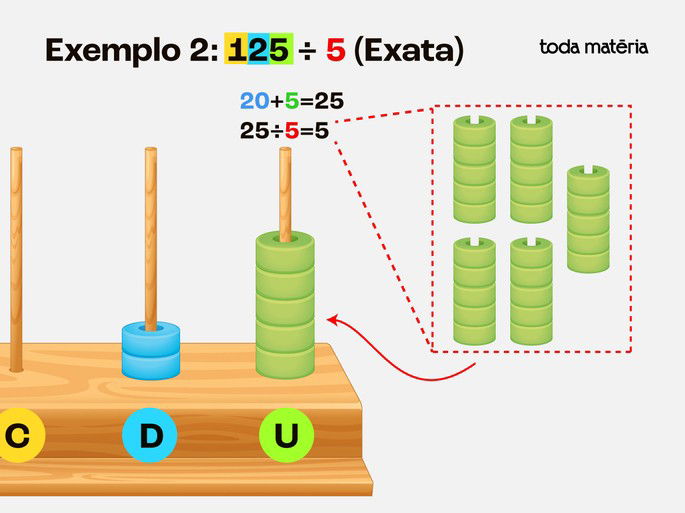
Passo 3: Troque 2 dezenas por 20 unidades, somando às 5 unidades - Agora temos 25 unidades.
Divida as 25 unidades em 5 grupos - Cada grupo recebe 5 unidades.
Exemplo 3: 99 ÷ 7 (Com resto)
Passo1: Coloque 9 dezenas e 9 unidades no ábaco.
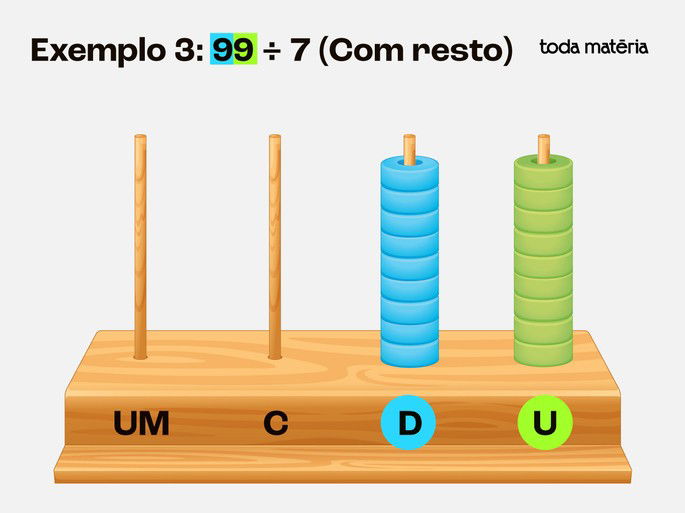
Passo 2: Divida as 9 dezenas em 7 grupos - Cada grupo recebe 1 dezena, sobra 2 dezenas.
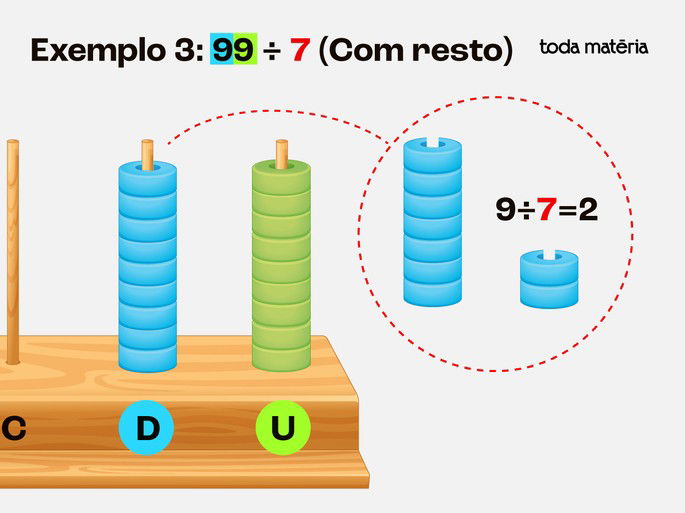
Passo 3: Troque 2 dezenas por 20 unidades, somando as 9 unidades - Agora temos 29 unidades.
Divida as 29 unidades em 7 grupos - Cada grupo recebe 4 unidades e sobra 1.
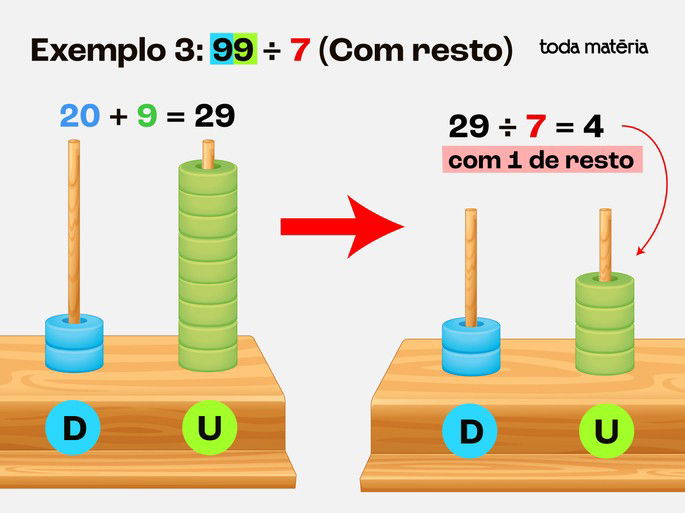
Passo 4: Avaliar o resultado: 99 ÷ 7=14 e resto 1.
A divisão no ábaco é feita dividindo as contas das hastes em partes iguais, representando o reagrupamento dos valores. Ou seja, vamos subtraindo grupos iguais e verificamos quantos grupos sobraram em cada haste.
História do ábaco
O ábaco surgiu há mais de 4.000 anos e foi um dos primeiros dispositivos criados para auxiliar nos cálculos matemáticos. Os sumérios e os babilônios já utilizavam tabelas de contagem com marcas em argila, um precursor do ábaco moderno. Posteriormente, os gregos e romanos desenvolveram versões mais sofisticadas, como a tábua de cálculos romana, que usava sulcos e pedras para representar números.
Na China, o ábaco conhecido como suan-pan foi amplamente utilizado desde a Dinastia Han (206 a.C. – 220 d.C.) e tornou-se um instrumento fundamental para comerciantes e acadêmicos. No Japão, uma versão modificada, chamada soroban, surgiu no século XV e é usada até hoje.
O ábaco também teve variantes na Rússia (antiga União Soviética), Índia e no Oriente Médio, sendo uma ferramenta fundamental até a popularização dos números indo-arábicos e das calculadoras modernas.
Continue estudando matemática com:
Atividades de matemática (para imprimir)
Atividades para desenvolver a habilidade EF04MA02 (composição e decomposição de números naturais).
Referências Bibliográficas
BEZERRA, Ricardo. Matemática Através dos Tempos: O Papel do Ábaco no Cálculo Matemático. Rio de Janeiro: Vozes, 2015.
GASPAR, José E. C. O Ábaco e a Matemática Moderna. São Paulo: Editora Ática, 2003.
SMOLE, Kátia Stocco; DINIZ, Maria Ignez. O Uso do Ábaco no Ensino da Matemática. São Paulo: Cortez Editora, 2010.
CANELLAS, William. Ábaco: entenda o que é e como funciona (aprenda a usar). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/abaco-historia-como-usar-operacoes/. Acesso em:


