Circunferência

Rafael C. Asth

Professor de Matemática e Física

Circunferência é uma figura geométrica com formato circular que faz parte dos estudos da geometria. Note que todos os pontos de uma circunferência são equidistantes de seu centro.

Assim, circunferência é o lugar geométrico do conjunto de todos os pontos que estão a uma distância fixa de um ponto central.

A circunferência é uma figura plana e fechada que, diferente do círculo, é apenas a linha. Já no círculo, incluímos sua área interna. Embora sejam conceitos diferentes, estão interligados e ambos possuem propriedades em comum.

Raio e diâmetro da circunferência

Lembre-se que o raio da circunferência é um segmento que liga o centro da figura a qualquer ponto localizado em sua extremidade.

Já o diâmetro da circunferência é um segmento de reta que passa pelo centro da figura, dividindo-a em duas metades. Por isso, o diâmetro equivale duas vezes o raio (2r).

A corda é um segmento de reta que passa pelo interior da circunferência, sem passar pelo centro e liga dois de seus pontos.

Comprimento da Circunferência

O comprimento da circunferência é a medida de seu entorno. Ele é proporcional ao raio, ou seja, quanto maior o raio, maior o comprimento.

Não confunda comprimento com diâmetro, enquanto o comprimento é a medida de uma volta completa, o diâmetro é a medida do segmento interno, que passa pelo centro.

A fórmula para calcular o comprimento da circunferência é:

• O é uma constante que, aproximadamente, vale 3,14;
• O r é a medida do raio.

Área do interior de uma circunferência (círculo)

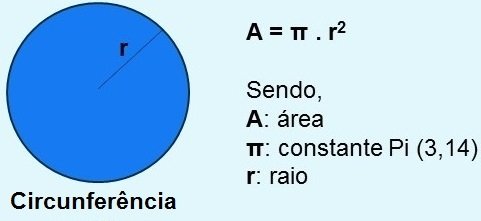
A área de uma figura determina o tamanho da superfície dessa figura. No caso da circunferência, a fórmula da área é:

Circunferência e Círculo

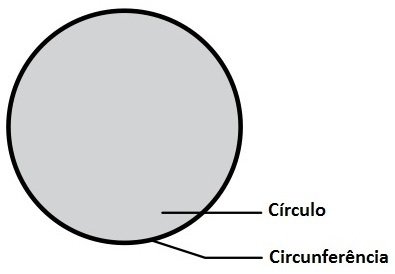
Muito comum haver confusão entre a circunferência e o círculo. Embora utilizemos esses termos como sinônimos, eles apresentam diferença.

Enquanto a circunferência representa a linha curva que limita o círculo (ou disco), este é uma figura limitada pela circunferência, ou seja, representa sua área interna.

Saiba mais sobre Área e Perímetro.

Equação Reduzida da Circunferência

A equação reduzida da circunferência é utilizada para determinar os diversos pontos de uma circunferência, auxiliando assim, em sua construção. Ela é representada pela seguinte expressão:

Onde as coordenadas de um ponto A que pertença à circunferência são os pontos (x, y) e de C, o centro, são os pontos (a, b). Na equação, r é a medida do raio.

Equação Geral da Circunferência

A equação geral da circunferência é dada a partir do desenvolvimento da equação reduzida.

Exercícios resolvidos de circunferência

Exercício 1

Calcule a área de uma circunferência com raio de 6 metros. Considere π = 3,14.

Exercício 2

Qual o perímetro de uma circunferência cujo raio mede 10 metros? Considere π = 3,14

Exercício 3

Se uma circunferência possui um raio de 3,5 metros, qual será seu diâmetro?

a) 5 metros
b) 6 metros
c) 7 metros
d) 8 metros
e) 9 metros

Exercício 4

Qual o valor do raio de uma circunferência cuja área equivale a 379,94 m²? Considere π = 3,14.

Exercício 5

Determine a equação geral da circunferência cujo centro possui as coordenadas C (2, –3) e raio r = 4.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.