Perímetro do Círculo

Rosimar Gouveia

Professora de Matemática e Física

O perímetro do círculo corresponde a medida da volta completa dessa figura geométrica plana. Nesse caso, o perímetro é o comprimento da circunferência.

Lembre-se se que o perímetro é a soma de todos os lados da figura. Por exemplo, se vamos encontrar o perímetro do triângulo, devemos somar o valor das medidas dos três lados da figura.

Fórmula do Perímetro

Vale lembrar que o círculo é uma figura que não apresenta segmentos de retas. Portanto, o perímetro do círculo equivale a soma total de seu contorno.

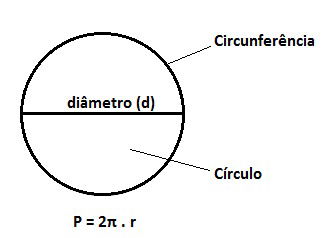
Assim, a fórmula é:

P = 2 π . r

Onde,

P: perímetro
π: constante de valor 3,14
r: raio

Fique Atento!

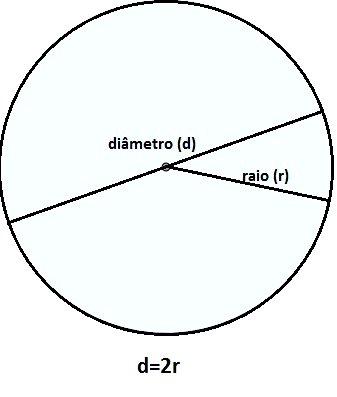
O valor do raio é determinante para encontrar o perímetro dessa figura. Assim, quanto maior o raio, maior será seu perímetro.

Feita essa observação, lembre-se que o raio é a medida do centro da figura até sua extremidade. Assim, o raio mede a metade do diâmetro.

Diferença entre Círculo e Circunferência

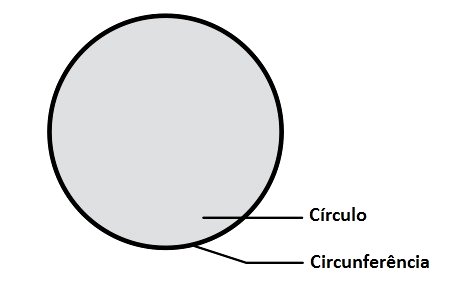
Embora muitas pessoas utilizam o termo círculo e circunferência como sinônimos, na matemática eles representam dois conceitos distintos.

• Círculo: é a parte interna da circunferência, ou seja, é a figura plana delimitada por ela.
• Circunferência: é o contorno (linha curva) que limita o círculo.

Exercícios Resolvidos

1. Calcule o perímetro de um círculo com diâmetro de 6 cm.

2. Determine o valor do diâmetro de um canteiro que apresenta perímetro de 20 m.

3. João percorre todos os dias 6 quilômetros em torno de um lago circular. No total, ele dá 12 voltas no local. Qual o valor do perímetro desse círculo em metros?

Que tal saber mais sobre:

• Número pi
• Comprimento da circunferência
• Área do Círculo
• Área e Perímetro
• Perímetros de Figuras Planas
• Áreas de Figuras Planas
• Perímetro do Retângulo

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.