Perímetros de Figuras Planas
Os perímetros de figuras planas indicam o valor da medida do contorno da figura. Ou seja, o conceito de perímetro corresponde à soma de todos os lados de uma figura geométrica plana.
Vejamos abaixo as principais figuras que fazem parte da Geometria Plana.
Principais Figuras Planas
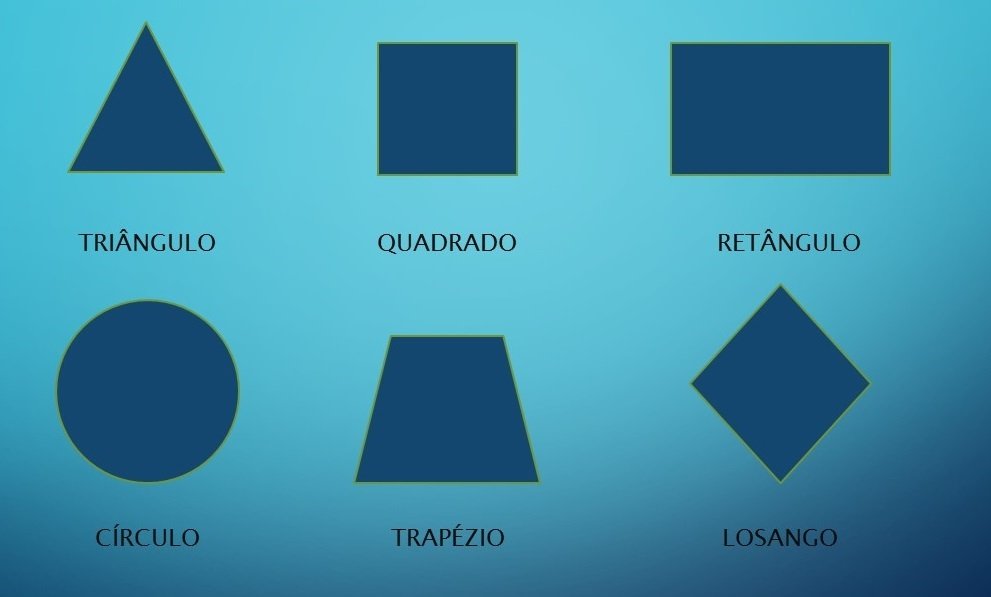
Triângulo
Figura plana formada por três lados e ângulos internos. De acordo com a medida dos lados eles podem ser:
- Triângulo Equilátero: lados e ângulos internos iguais (60°);
- Triângulo Isósceles: dois lados e dois ângulos internos congruentes;
- Triângulo Escaleno: todos os lados e ângulos internos são diferentes.
E, de acordo com a medida dos ângulos, eles são classificados em:
- Triângulo Retângulo: um ângulo interno de 90°;
- Triângulo Obtusângulo: dois ângulos agudos internos (menor que 90°), e um ângulo obtuso interno (maior que 90°);
- Triângulo Acutângulo: três ângulos internos menores que 90°.
Leia mais:
Quadrado
Figura plana formada por quatro lados congruentes (mesma medida). Possui quatro ângulos internos de 90° (ângulos retos).
Leia mais:
Retângulo
Figura plana formada por quatro lados, donde dois deles são menores. Também possui quatro ângulos internos de 90°.
Leia mais:
Círculo
Figura plana que também é chamada de disco. É formado pelo raio (distância entre o centro e a extremidade da figura) e o diâmetro (segmento de reta que passa pelo centro e vai de um lado ao outro da figura.
Leia mais:
Trapézio
Figura plana formada por quatro lados. Apresenta dois lados e bases paralelas, sendo uma menor e outra maior. De acordo com a medida dos lados e ângulos eles são classificados em:
- Trapézio Retângulo: possui dois ângulos de 90º;
- Trapézio Isósceles ou Simétrico: os lados não paralelos possuem a mesma medida;
- Trapézio Escaleno: todos os lados possuem medidas diferentes.
Leia mais:
Losango
Figura plana formada por quatro lados iguais. Possui lados e ângulos opostos congruentes e paralelos.
Saiba sobre a Área do Losango.
Perímetro e Área de Figuras Planas
É comum haver confusão entre o conceito de área e perímetro. No entanto, a área é a medida da superfície de uma figura plana. Já o perímetro é soma das medidas dos lados da figura.
Saiba mais sobre o tema:
Fórmulas dos Perímetros
Para calcular cada uma das figuras planas apresentadas acima, utilizam-se as seguintes fórmulas:
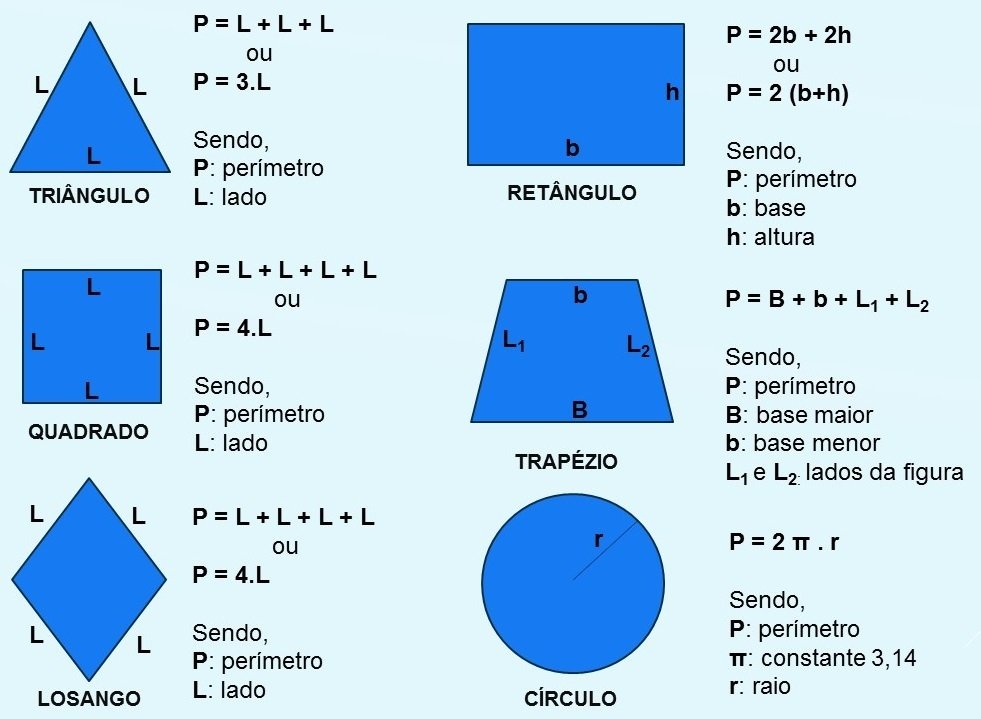
Leia também sobre Quadriláteros.
Exercício Resolvido
Confira abaixo um exercício que caiu no Enem e envolve tanto o conceito de perímetro quanto o de área:
(Enem-2011) Em uma certa cidade, os moradores de um bairro carente de espaços de lazer reivindicam à prefeitura municipal a construção de uma praça. A prefeitura concorda com a solicitação e afirma que irá construí-la em formato retangular devido às características técnicas do terreno. Restrições de natureza orçamentária impõem que sejam gastos, no máximo, 180 m de tela para cercar a praça. A prefeitura apresenta aos moradores desse bairro as medidas dos terrenos disponíveis para a construção da praça:
Terreno 1: 55 m por 45 m
Terreno 2: 55 m por 55 m
Terreno 3: 60 m por 30 m
Terreno 4: 70 m por 20 m
Terreno 5: 95 m por 85 m
Para optar pelo terreno de maior área, que atenda às restrições impostas pela prefeitura, os moradores deverão escolher o terreno.
a) 1
b) 2
c) 3
d) 4
e) 5
Confira mais questões, com resolução comentada, em Exercícios sobre Área e Perímetro.
GOUVEIA, Rosimar. Perímetros de Figuras Planas. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/perimetros-de-figuras-planas/. Acesso em:



