Trapézio
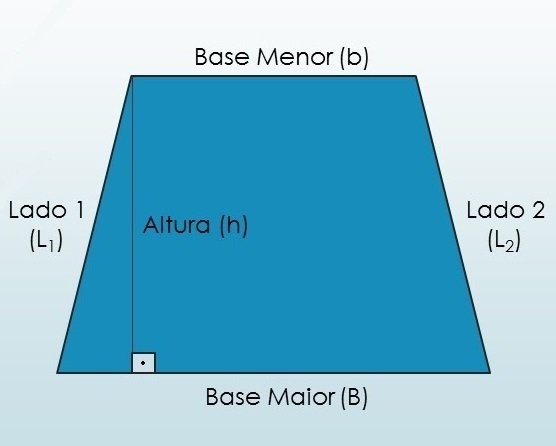
O trapézio é uma figura da geometria plana formada por quatro lados. Dois deles são paralelos e chamados de bases. Ele é considerado um quadrilátero, tal qual o retângulo, o losango e o quadrado.
Importante destacar que ele é chamado de quadrilátero notável. Isso porque a soma de seus quatro ângulos internos totaliza 360°.
Tipos de Trapézio
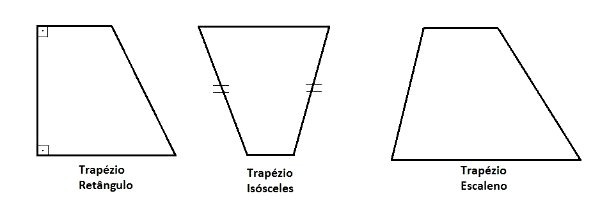
Dependendo de sua forma, o trapézio é classificado de três maneiras:
- Trapézio Retângulo: esse tipo de trapézio apresenta dois ângulos de 90°, chamados de ângulos retos.
- Trapézio Isósceles: também chamado de trapézio simétrico, ele apresenta dois lados congruentes (possuem a mesma medida) e dois lados diferentes.
- Trapézio Escaleno: todos os lados desse trapézio apresentam medidas diferentes.
Saiba mais sobre as figuras geométricas:
Área do Trapézio
Para medir o valor da superfície do trapézio utilizamos a seguinte fórmula:

Onde:
A: área da figura
B: base maior
b: base menor
h: altura
Saiba mais sobre a Área do Trapézio.
Perímetro do Trapézio
Para calcular o perímetro do trapézio, ou seja, a soma de todos os lados, utiliza-se a fórmula:

Onde:
P: perímetro
B: base maior
b: base menor
L1e L2: lados da figura
Que tal saber mais sobre o tema? Leia também:
Base Média do Trapézio
Quando um segmento de reta corta o trapézio em duas figuras, temos a chamada base média de um trapézio. Esse segmento é paralelo as bases da figura.

Para encontrar o valor da base média do trapézio utilizamos a seguinte fórmula:

Curiosidade: Você Sabia?
Na anatomia, o trapézio é um músculo triangular que fica na região posterior da coluna cervical.
Exercícios Resolvidos
1. Calcule a área de um trapézio com altura de 8 cm e bases de 10 cm e 5 cm.
2. Calcule o perímetro de um trapézio com bases de 12 cm e 9 cm e lados de 15 cm e 16 cm.
GOUVEIA, Rosimar. Trapézio. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/trapezio/. Acesso em:


