Área do Trapézio

Rosimar Gouveia

Professora de Matemática e Física

A área do trapézio mede o valor da superfície dessa figura plana formada por quatro lados.

O trapézio é um quadrilátero que possui dois lados e duas bases paralelas, sendo que uma é maior e outra menor.

O trapézio é considerado um quadrilátero notável, de forma que a soma de seus ângulos internos corresponde a 360°.

Classificação dos Trapézios

Os trapézios são classificados em três tipos:

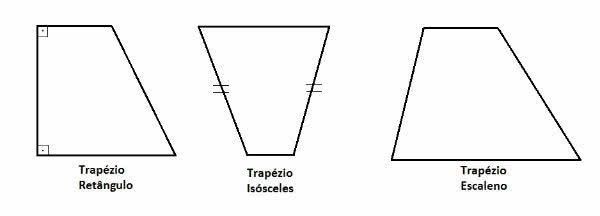
• Trapézio Retângulo: apresenta dois ângulos de 90º, chamados de ângulos retos.
• Trapézio Isósceles ou Simétrico: os lados não paralelos são congruentes (possuem a mesma medida).
• Trapézio Escaleno: todos os lados possuem medidas diferentes.

Fórmula da Área

Para calcular a área do trapézio utilizamos a seguinte fórmula:

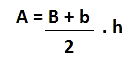
Onde:

A: área da figura
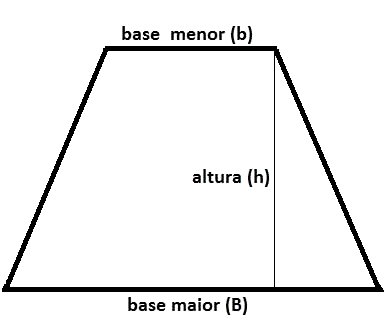
B: base maior
b: base menor
h: altura

Fórmula do Perímetro

Para calcular o perímetro do trapézio utiliza-se a fórmula:

P = B + b + L₁ + L₂

Onde:

P: perímetro (soma de todos os lados)
B: base maior
b: base menor
L₁ e L_2: lados da figura

Saiba mais sobre o tema nos artigos:

• Trapézio
• Geometria Plana
• Área e Perímetro
• Área dos Polígonos
• Perímetros de Figuras Planas
• Áreas de Figuras Planas
• Área de Figuras Planas - Exercícios

Exercícios Resolvidos

1. Calcule a área de um trapézio de altura 5 cm e bases de 8 cm e 3 cm.

2. Determine a medida da base menor de um trapézio de 100 cm² de área, 10 cm de altura e base maior de 15 cm.

3. Qual a altura de um trapézio com área de 50 cm², base maior de 6 cm e menor de 4 cm?

Que tal saber mais sobre as áreas de outras figuras planas?

• Área do Círculo
• Área do Triângulo
• Área do Losango
• Área do Quadrado
• Área do Retângulo
• Área do Paralelogramo
• Fórmulas de Matemática

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.