Área do Quadrado

Rosimar Gouveia

Professora de Matemática e Física

A área do quadrado corresponde ao tamanho da superfície dessa figura. Lembre-se que o quadrado é um quadrilátero regular que apresenta quatro lados congruentes (mesma medida).

Além disso, ele possui quatro ângulos internos de 90°, chamados de ângulos retos. Assim, a soma dos ângulos internos do quadrado totaliza 360°.

Fórmula da Área

Para calcular a área do quadrado, basta multiplicar a medida de dois lados (l) dessa figura. Muitas vezes os lados são chamados de base (b) e altura (h). No quadrado a base é igual à altura (b=h). Logo, temos a fórmula da área:

A = L²
ou
A = b.h

Observe que o valor geralmente será dado em cm² ou m². Isso porque o cálculo corresponde a multiplicação entre duas medidas. (cm . cm = c² ou m . m = m²)

Exemplo:

Encontra a área de um quadrado com 17 cm de lado.

A = 17 cm . 17 cm
A = 289 cm²

Veja também outros artigos de áreas de figuras planas:

• Área dos Polígonos
• Área do Retângulo
• Área do Triângulo
• Área do Círculo
• Área do Trapézio
• Área do Losango
• Áreas de Figuras Planas
• Área de Figuras Planas - Exercícios

Fique Atento!

Diferente da área, o perímetro de uma figura plana é encontrado por meio da soma de todos os lados.

No caso do quadrado, o perímetro é soma dos quatro lados, dado pela expressão:

P = L + L + L + L
ou
P = 4L

Obs: Note que o valor do perímetro geralmente é dado em centímetros (cm) ou metros (m). Isso porque o cálculo para encontrar o perímetro corresponde a soma de seus lados.

Exemplo:

Qual o Perímetro de um quadrado com 10 m de lado?

P = L + L + L + L
P = 10 m + 10 m + 10 m + 10 m
P = 40 m

Saiba mais sobre o tema em:

• Área e Perímetro
• Perímetro do Quadrado
• Perímetros de Figuras Planas

Diagonal do Quadrado

A diagonal do quadrado representa o segmento de reta que corta a figura em duas partes. Quando isso ocorre o que temos são dois triângulos retângulos.

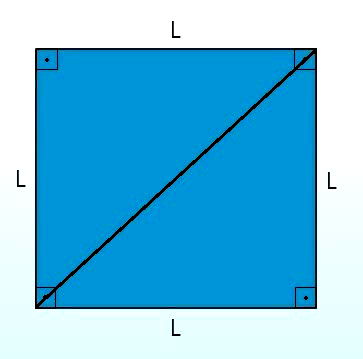
Os triângulos retângulos são um tipo de triângulo que apresentam um ângulo interno de 90° (chamado de ângulo reto).

De acordo com o Teorema de Pitágoras a hipotenusa elevada ao quadrado é igual a soma de seus catetos elevados ao quadrado. Logo:

A² = b² + c²

Nesse caso, “a” é a diagonal do quadrado que corresponde a hipotenusa. Ela é o lado oposto ao ângulo de 90º.

Já os catetos oposto e adjacente correspondem aos lados da figura. Feita essa observação, podemos encontrar a diagonal por meio da fórmula:

d² = L² + L²
d² = 2L²
d = √2L²
d = L√2

Assim, se tivermos o valor da diagonal podemos encontrar a área de um quadrado.

Exercícios Resolvidos

1. Calcule a área de um quadrado com lado de 50 m.

2. Qual a área de um quadrado cujo perímetro é de 40 cm?

3. Encontre a área de um quadrado cuja diagonal mede 4√2 m.

Conheça também outras figuras geométricas nos artigos:

• O que é um quadrado? Definição, fórmulas e exercícios
• Geometria Plana
• Retângulo
• Geometria Espacial
• Fórmulas de Matemática

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.