Área dos Polígonos

Rafael C. Asth

Professor de Matemática e Física

Os polígonos são figuras geométricas planas formadas pela união de segmentos de reta e a área representa a medida de sua superfície.

As unidades de área são medidas lineares ao quadrado, como:

$reto m ao quadrado$ : metro quadrado
$cm ao quadrado$ : centímetro quadrado

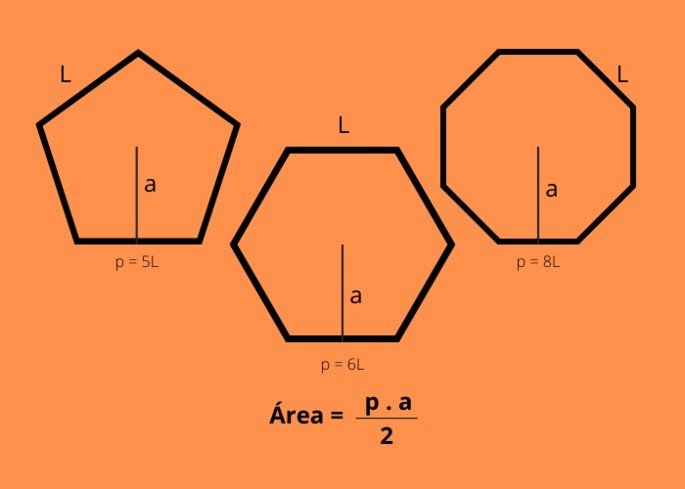
Para realizar o cálculo da área dos polígonos são necessários alguns dados. No caso dos perímetros de polígonos regulares, o cálculo geral da área é: o semiperímetro multiplicado pelo apótema.

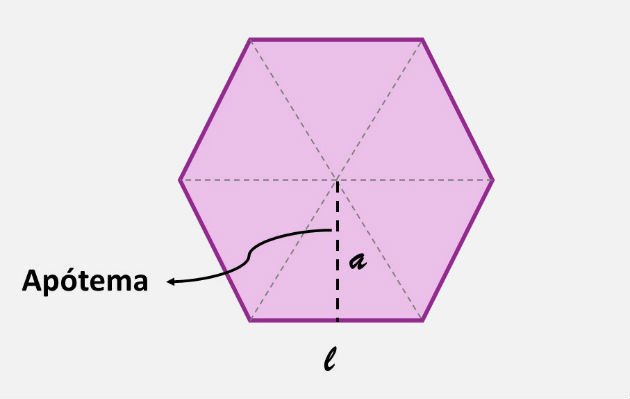
Apótema de um polígono — Apótema de um hexágono

Apótema = a
Lado = L
Perímetro = 6 . L (hexágono)
Semiperímetro p = perímetro : 2
Área = p . a

O perímetro representa a soma dos lados de um polígono, assim, o semiperímetro é a metade do perímetro. O apótema é um segmento de reta que une o centro do polígono ao meio de um dos lados.

Os polígonos regulares são que possuem todos os lados e ângulos de mesma medida.

Para calcular a áreas dos polígonos regulares, a fórmula geral é: semiperímetro multiplicado pelo apótema.

$reto A igual a reto P sobre 2 espaço. espaço a$

Onde,
P/2 é o semiperímetro (metade do perímetro),
a é a medida do apótema.

Área do hexágono

No caso de um hexágono regular, nota-se que ele é formado pela união de seis triângulos equiláteros. A fórmula da área de um triângulo equilátero é

$reto L ao quadrado espaço. espaço numerador √ 3 sobre denominador 4 fim da fração espaço$

Desse modo, o hexágono possui seis vezes a área de um triangulo equilátero:

$6 abre parênteses reto L ao quadrado espaço. espaço numerador √ 3 sobre denominador 4 fim da fração espaço fecha parênteses$

Simplificando

$começar estilo tamanho matemático 18px 3 reto L ao quadrado numerador raiz quadrada de 3 sobre denominador 2 fim da fração espaço fim do estilo$

Área de um quadrado ou retângulo

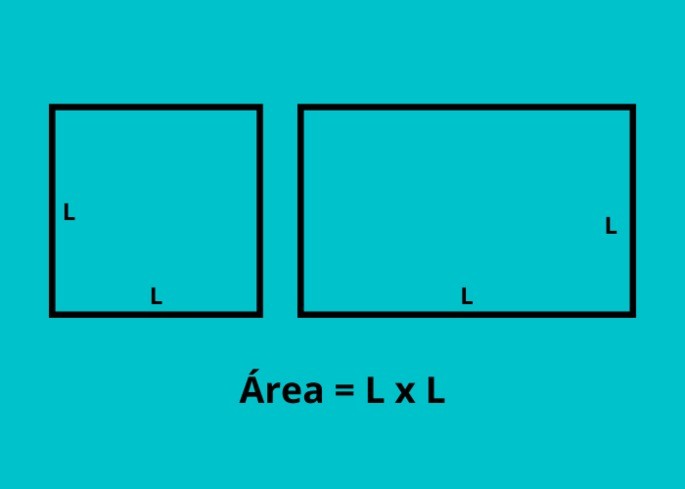
A área de um quadrilátero com ângulos congruentes (90º), que é o caso do quadrado e do retângulo, é dada pela multiplicação de dois dos lados.

Retângulo: o lado maior vezes o lado menor (L x l).
Quadrado: por ser o único quadrilátero regular, sua área dada por L²ou L x L.

Veja também Área do Quadrado.

Área de um Paralelogramo

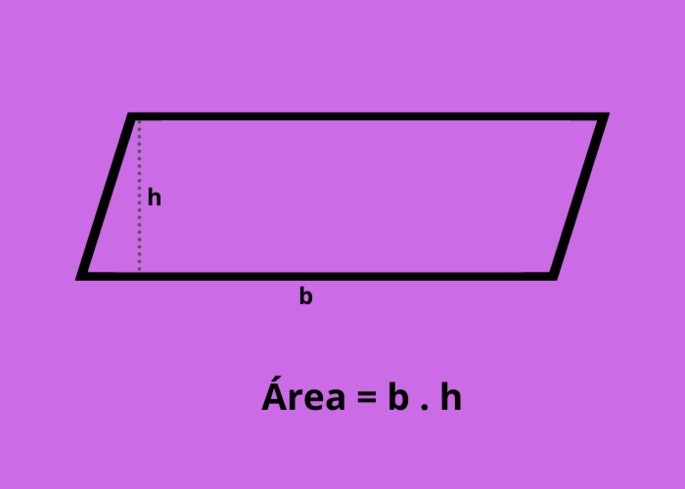
A área do paralelogramo é calculada pela base vezes a altura.

Área de um Trapézio

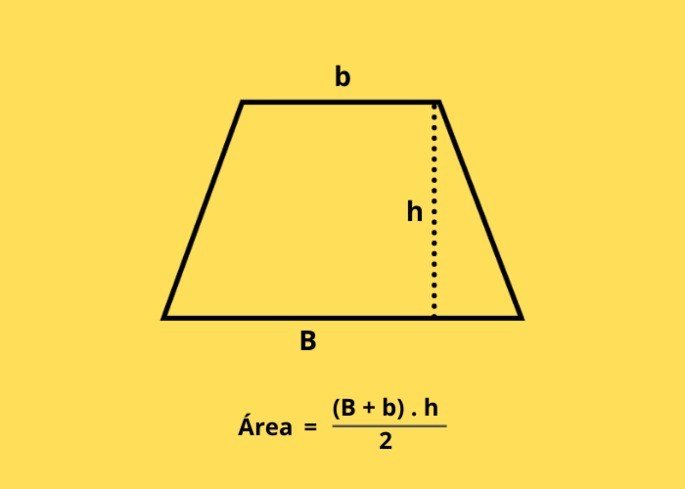
A área do trapézio é dada pela soma de suas bases (maior e menor), vezes a altura, divida por dois.

Veja também: Área do Trapézio.

Área de um Losango

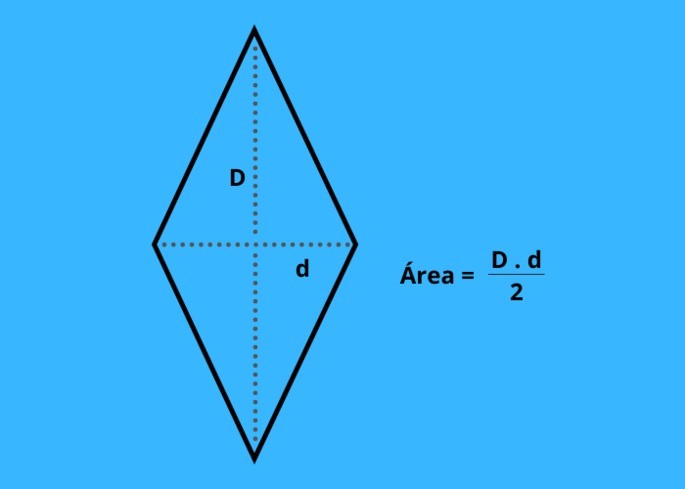
Para calcular a área de um losango basta multiplicar a diagonal maior pela diagonal menor e dividir por 2.

Área de um Triângulo

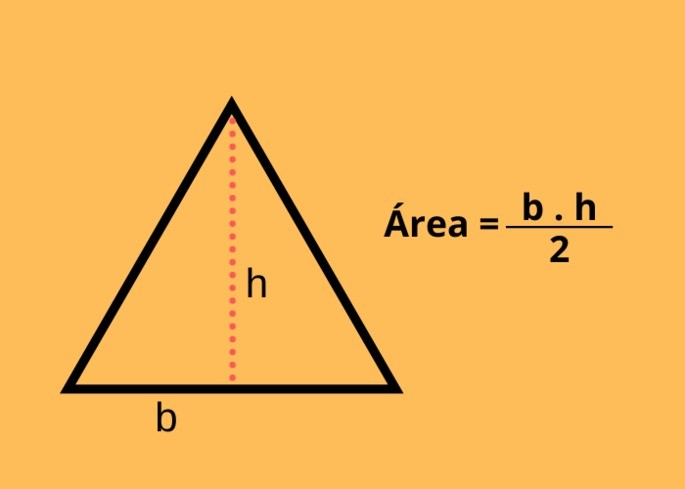
A área do triângulo é calculada a partir da base vezes a altura, dividido por dois.

Fórmula de Herón para área de triângulos

$começar estilo tamanho matemático 18px reto A igual a raiz quadrada de reto p. parêntese esquerdo reto p menos reto a parêntese direito. parêntese esquerdo reto p menos reto b. parêntese esquerdo reto p menos reto c parêntese direito fim da raiz fim do estilo$

Onde,
p é o semiperímetro e a, b e c são os lados.

Triângulo retângulo

Por possuir um ângulo reto (semelhante à altura), sua área pode ser calculada por: (cateto oposto x cateto adjacente) : 2.

Triângulo Isósceles

No caso de um triângulo isósceles, deve-se usar a fórmula geral de área de um triângulo qualquer, mas se a altura não for dada, deve-se utilizar o teorema de pitágoras.

No triângulo isósceles, a altura relativa à base (lado com medida diferente) dividirá este lado em dois segmentos de mesma medida, possibilitando a aplicação do teorema.

Triângulo equilátero

Como dito anteriormente, a área de um triângulo equilátero (lados iguais) pode ser calculada a partir da medida de seus lados, utilizando o teorema de pitágoras:

$L ao quadrado igual a h ao quadrado mais abre parênteses L sobre 2 fecha parênteses ao quadrado seta dupla para a direita h ao quadrado igual a L ao quadrado menos L sobre 4 ao quadrado seta dupla para a direita h igual a índice radical espaço em branco de numerador 3 L ao quadrado sobre denominador 4 fim da fração fim da raiz seta dupla para a direita h igual a numerador raiz quadrada de 3 espaço L sobre denominador 2 fim da fração$

Desse modo, aplicando a fórmula básica de cálculo da área dos triângulos temos:

$Á r e a espaço igual a espaço numerador L. h sobre denominador 2 fim da fração espaço igual a espaço L. espaço numerador raiz quadrada de 3. espaço L sobre denominador 2 fim da fração igual a espaço L ao quadrado. numerador espaço raiz quadrada de 3 sobre denominador 4 fim da fração$

Veja também: Área do Triângulo.

Área de um Polígono Côncavo

Para calcular a área de um polígono côncavo, é necessário utilizar o conhecimento sobre o cálculo da área de outros polígonos.

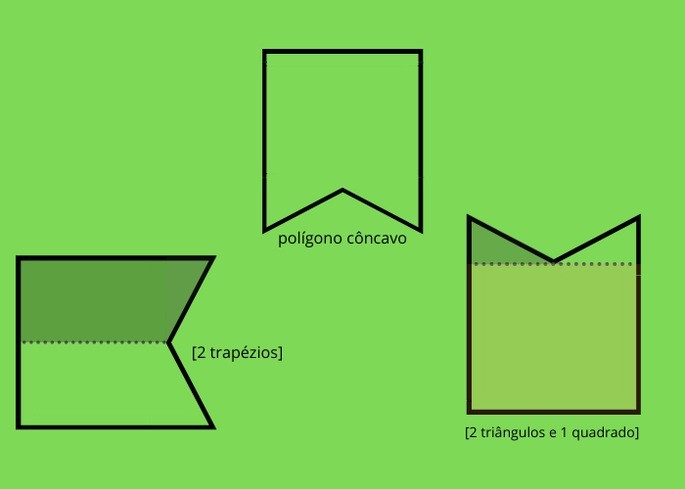
Assim, é necessário adaptar as fórmulas aos dados apresentados e aplicar a fórmula de acordo com o modo de divisão do polígono.

Interessou? Veja também:

Pratique

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações