Polígonos: o que são e suas classificações (com exemplos)

Rafael C. Asth

Professor de Matemática e Física

Os polígonos são figuras planas e fechadas constituídas por segmentos de reta. O estudo dos polígonos pertence à geometria plana.

Um polígono é uma forma geométrica plana, formada por uma linha poligonal, ou seja, seguimentos de retas. Por isso, não há curvas em um polígono.

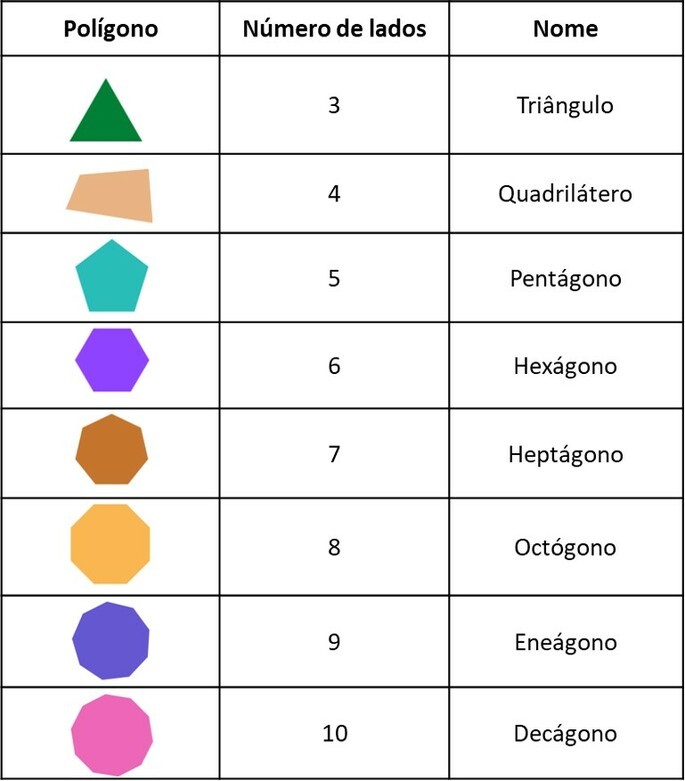
Há diversas formas para classificar um polígono, sendo muito usual classificá-los quanto ao número de lados. Por exemplo, todo polígono com três lados é classificado como triângulo, enquanto todo com quatro lados, como quadriláteros.

Conforme a classificação quanto ao número de lados, os polígonos recebem nomes. Aqui estão alguns.

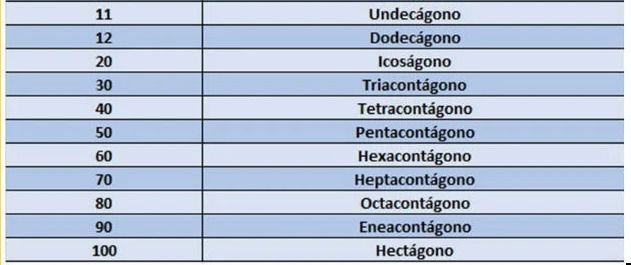
Um polígono por ter muitos lados, e conforme a quantidade, torna-se pouco prático ilustrá-los. Veja os nomes de mais alguns polígonos.

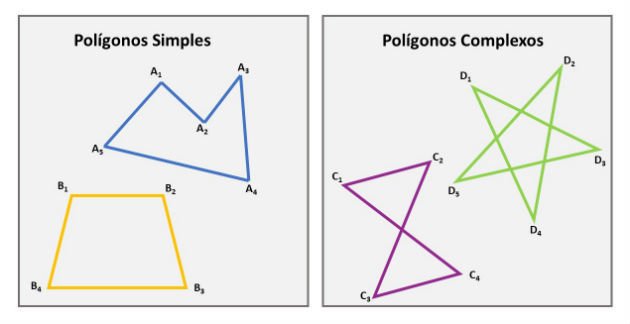
Os polígonos podem ser simples ou complexos, sendo os simples aqueles cujos segmentos consecutivos que os formam não sejam colineares, não se cruzem. Os segmentos que formam os polígonos encontram-se apenas nas extremidades.

Quando existe intersecção entre dois lados não consecutivos, o polígono é chamado de complexo.

Polígono convexo e côncavo

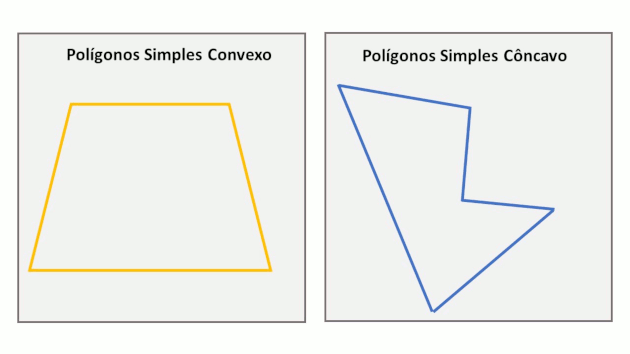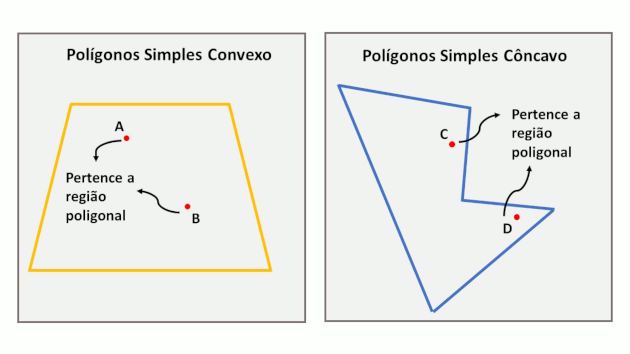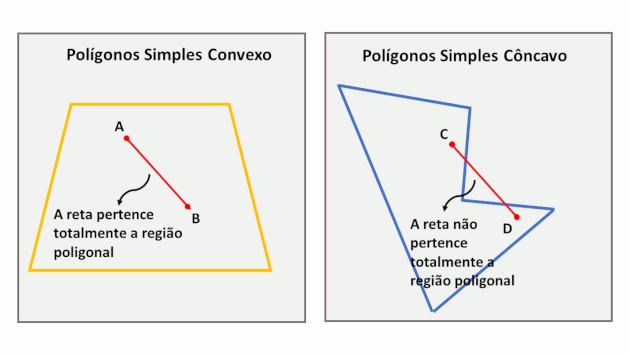
A junção das retas que formam os lados de um polígono com o seu interior é chamada de região poligonal. Essa região pode ser convexa ou côncava.

Os polígonos simples são chamados de convexos quando qualquer reta que une dois pontos, pertencente a região poligonal, ficará totalmente inserida nesta região. Já nos polígonos côncavos isso não acontece.

Polígonos regulares

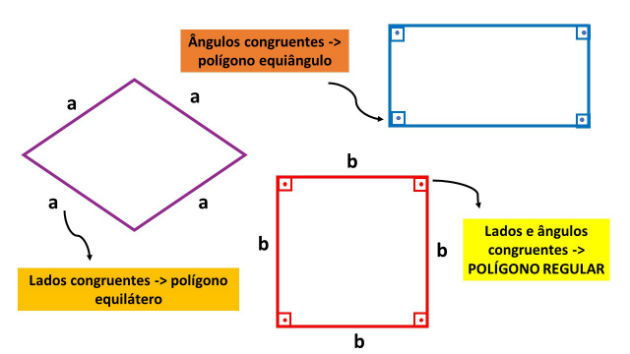
Os polígonos são regulares quando todos seus lados são iguais, de mesma medida, assim como seus ângulos, que devem possuir medidas iguais.

Quando um polígono apresenta todos os lados congruentes entre si, ou seja, possuem a mesma medida, ele é chamado de equilátero. Quando todos os ângulos têm mesma medida, ele é chamado de equiângulo.

Os polígonos convexos são regulares quando apresentam os lados e os ângulos congruentes, ou seja, simultaneamente equiláteros e equiângulos. Por exemplo, o quadrado é um polígono regular.

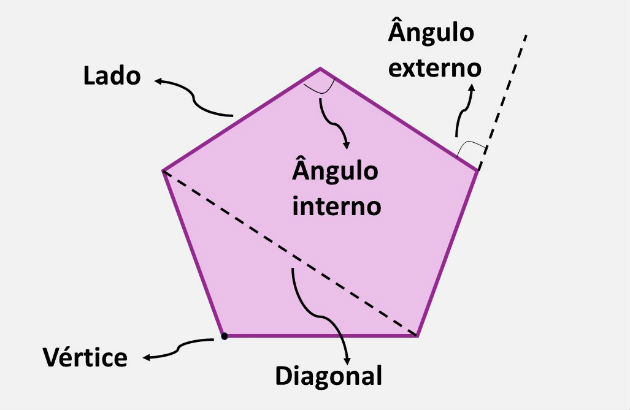
Elementos do Polígono

• Vértice: corresponde ao ponto de encontro dos segmentos que formam o polígono.
• Lado: corresponde a cada segmentos de reta que une vértices consecutivos.
• Ângulos:
  • Os ângulos internos correspondem aos ângulos formados por dois lados consecutivos. Por outro lado,
  • Os ângulos externos são os ângulos formados por um lado e pelo prolongamento do lado sucessivo a ele.
• Diagonal: corresponde ao segmento de reta que liga dois vértices não consecutivos, ou seja, um segmento de reta que passa pelo interior da figura.

Saiba mais sobre os Quadriláteros.

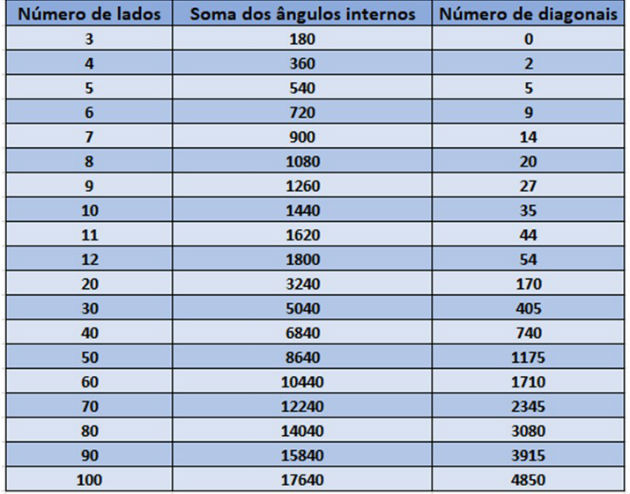
Soma dos ângulos internos de um polígono

A soma dos ângulos externos dos polígonos convexos é sempre igual a 360º. Entretanto, para obter a soma dos ângulos internos de um polígono é necessário aplicar a seguinte fórmula:

Sendo n o número de lados.do polígono.

Exemplo
Qual é o valor da soma dos ângulos internos de um icoságono convexo?

Resolução
O icoságono convexo é um polígono que apresenta 20 lados, ou seja, n = 20. Aplicando esse valor na fórmula, temos:

Assim, a soma dos ângulos internos do icoságono é igual a 3240º.

Cálculo do número de diagonais

Para calcular o número de diagonais de um polígono, utiliza-se a seguinte fórmula:

Exemplo
Quantas diagonais apresenta um octógono convexo?

Resolução
Considerando que o octógono possui 8 lados, aplicando a fórmula, temos:

Portanto, um octógono convexo contém 20 diagonais.

Na tabela abaixo, temos o valor da soma dos ângulos internos e o número de diagonais dos polígonos convexos conforme o número de lados de alguns polígonos.

Perímetro e área dos polígonos

O perímetro é a soma das medidas de todos os lados de uma figura. Assim, para conhecer o perímetro de um polígono, basta somar as medidas dos lados que o compõe.

A área é definida como a medida de sua superfície. Para encontrar o valor da área de um polígono, utilizamos fórmulas específicas, segundo o polígono que está sendo calculado.

Por exemplo, a área do retângulo é encontrada multiplicando-se a medida da largura pelo comprimento.

Já a área do triângulo é igual à multiplicação da base pela altura e o resultado dividido por 2.

Para saber como calcular a área de outras polígonos, leia também área dos polígonos.

Fórmula da área do polígono a partir do perímetro

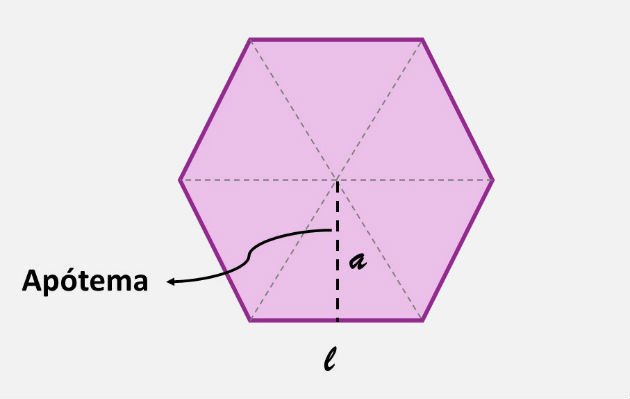
Quando conhecemos o valor do perímetro de um polígono regular, podemos utilizar a seguinte fórmula para calcular a sua área:

Sendo p o semiperímetro (a medida do perímetro dividido por 2) e a o apótema.

Veja também: Polígonos regulares.

Exercícios sobre polígonos resolvidos

Exercício 1

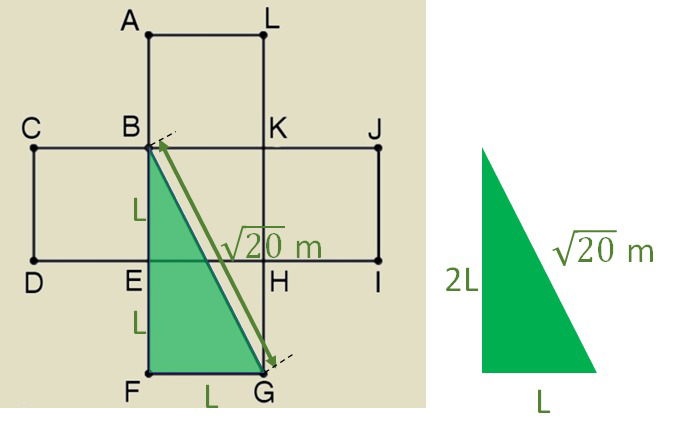
(CEFET/RJ - 2016) O quintal da casa de Manoel é formado por cinco quadrados ABKL, BCDE, BEHK, HIJK e EFGH, de igual área e tem a forma da figura ao lado. Se , então a área do quintal é:

a) 20 m²
b) 30 m²
c) 40 m²
d) 50 m²

Pratique mais

• Diagonais de um polígono: o que são e como calcular
• Polígonos convexos: o que são e como reconhecer um
• Exercícios sobre polígonos.
• Soma dos ângulos internos de um polígono

Para saber mais, leia também

• Formas Geométricas
• Simetria: tipos, definição e atividades para imprimir

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.