Área do Hexágono

Rafael C. Asth

Professor de Matemática e Física

Hexágono é um polígono que possui seis lados delimitados por segmentados de reta. Essa figura plana é formada pela junção de seis triângulos equiláteros.

Quando o hexágono é regular todos os lados possuem a mesma medida e seus ângulos internos são de 120º. Por isso, a área do hexágono é seis vezes a área de um triângulo equilátero que o compõe.

Como calcular a área do hexágono regular?

A fórmula para calcular a área do hexágono é:

$começar estilo tamanho matemático 22px reto A com reto h subscrito espaço igual a numerador 3 reto L ao quadrado raiz quadrada de 3 sobre denominador 2 fim da fração fim do estilo$

Onde, $reto A com reto h subscrito$ é área e L é a medida do lado hexágono.

Dessa forma a área do hexágono só depende da medida do lado.

Veja a seguir os passos para chegar nessa fórmula.

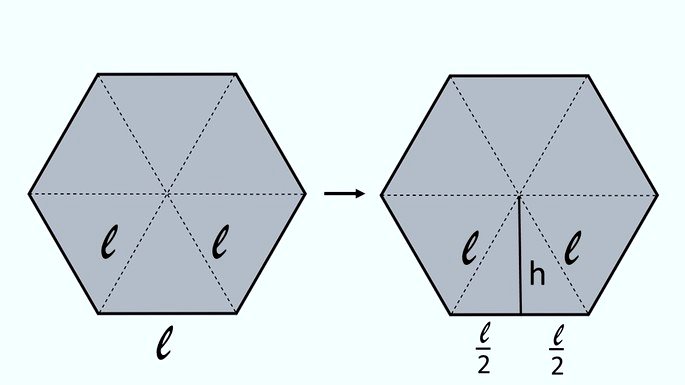
O hexágono regular pode ser dividido em seis triângulos equiláteros

O triângulo equilátero possui três lados com a mesma medida. Quando traçamos uma linha, representando a altura (h), dividimos um triângulo equilátero em outros dois triângulos.

Aplicando o Teorema de Pitágoras, encontramos a altura do triângulo da seguinte forma:

$reto L ao quadrado espaço igual a espaço reto h ao quadrado espaço mais espaço parêntese esquerdo reto L sobre 2 parêntese direito ao quadrado espaço reto h ao quadrado espaço igual a espaço reto L ao quadrado espaço menos espaço reto L ao quadrado sobre 4 reto h ao quadrado espaço igual a numerador 4 espaço reto L ao quadrado espaço menos reto L ao quadrado espaço sobre denominador 4 fim da fração igual a numerador 3 reto L ao quadrado sobre denominador 4 fim da fração reto h espaço igual a espaço raiz quadrada de numerador 3 reto L ao quadrado sobre denominador 4 fim da fração fim da raiz espaço reto h espaço igual a espaço numerador raiz quadrada de 3 sobre denominador 2 fim da fração reto L$

A fórmula para calcular a área do triângulo é:

$reto A com reto t subscrito espaço igual a numerador espaço base espaço reto x espaço altura sobre denominador 2 fim da fração$

Substituindo os termos, temos:

$reto A com reto t subscrito espaço igual a numerador reto L espaço reto x espaço começar estilo mostrar numerador raiz quadrada de 3 sobre denominador 2 fim da fração fim do estilo reto L sobre denominador 2 fim da fração reto A com reto t subscrito espaço igual a espaço numerador reto L ao quadrado raiz quadrada de 3 sobre denominador 2 fim da fração reto x espaço 1 meio reto A com reto t subscrito espaço igual a numerador reto L ao quadrado raiz quadrada de 3 sobre denominador 4 fim da fração$

Como o hexágono é formado por seis triângulos equiláteros, a área do hexágono é seis vezes a área do triângulo. Veja:

$espaço reto A com reto h subscrito espaço igual a espaço 6 espaço reto x espaço numerador reto L ao quadrado espaço raiz quadrada de 3 sobre denominador 4 fim da fração reto A com reto h subscrito espaço igual a espaço numerador 6 reto L ao quadrado espaço raiz quadrada de 3 sobre denominador 4 fim da fração tabela linha com célula com dividido por 2 fim da célula linha com célula com dividido por 2 fim da célula fim da tabela negrito A com negrito h subscrito negrito espaço negrito igual a numerador negrito 3 negrito L à potência de negrito 2 raiz quadrada de negrito 3 sobre denominador negrito 2 fim da fração$

Exercício resolvido

Para fazer um hexágono Pedro cortou uma cartolina. Com uma régua mediu e verificou que todos os lados tinham 10 cm. Qual a área do hexágono que Pedro criou?

Ver Resposta

Resposta correta: $150 raiz quadrada de 3 espaço cm ao quadrado$

Para resolver esse exemplo basta apenas substituir a medida do lado, 10 cm, na fórmula para calcular a área.

$reto A com reto h subscrito espaço igual a numerador 3 reto L ao quadrado raiz quadrada de 3 sobre denominador 2 fim da fração reto A com reto h subscrito espaço igual a numerador 3 espaço reto x espaço 10 ao quadrado raiz quadrada de 3 sobre denominador 2 fim da fração reto A com reto h subscrito espaço igual a numerador 300 raiz quadrada de 3 sobre denominador 2 fim da fração reto A com reto h subscrito espaço igual a 150 raiz quadrada de 3 espaço cm ao quadrado$

Você também pode se interessar por:

Como calcular a área de um hexágono a partir do apótema

Outra forma de calcular a área de um hexágono é utilizando o perímetro e o apótema. A fórmula utilizada é:

$negrito A com negrito h subscrito negrito espaço negrito igual a negrito espaço negrito p sobre negrito 2 negrito x negrito espaço negrito alfa$

Sendo $reto alfa espaço igual a numerador reto r raiz quadrada de 3 sobre denominador 2 fim da fração$

O perímetro (p) corresponde à soma dos lados do polígono, já o apótema ( $alfa$ ) é encontrado traçando uma linha entre o centro do hexágono e o ponto médio de um dos lados da figura.

Quando um hexágono regular está inscrito em uma circunferência, os seis vértices da figura dividem a circunferência em seis partes iguais. Neste caso, o raio da circunferência (r) coincide com o lado do hexágono (l), pois formam um triângulo equilátero $incremento OAB$ .

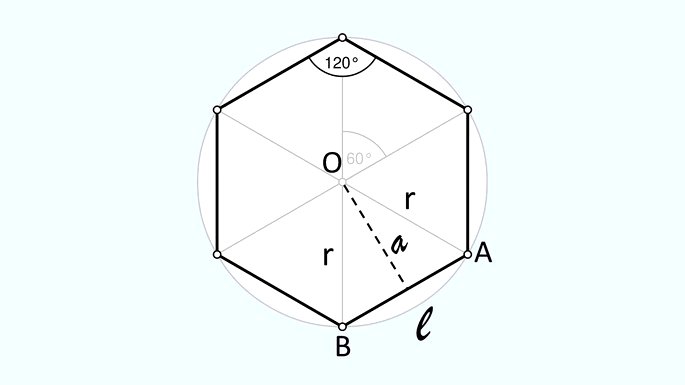
Sendo $AB sobre 2 igual a reto r sobre 2$ , aplicamos o Teorema de Pitágoras e encontramos a fórmula para calcular o apótema da seguinte forma:

$reto r ao quadrado espaço igual a espaço reto alfa ao quadrado espaço mais espaço reto r ao quadrado sobre 4 reto alfa ao quadrado espaço igual a reto r ao quadrado espaço espaço menos espaço reto r ao quadrado sobre 4 igual a espaço numerador 3 reto r ao quadrado sobre denominador 4 fim da fração reto alfa ao quadrado espaço igual a raiz quadrada de numerador 3 reto r ao quadrado sobre denominador 4 fim da fração fim da raiz negrito alfa negrito espaço negrito igual a numerador negrito r raiz quadrada de negrito 3 sobre denominador negrito 2 fim da fração$

Exercício resolvido

Em uma circunferência cujo raio mede 10 cm, foi desenhado um hexágono regular. Calcule as medidas de lado, apótema e área do polígono desenhado.

Ver Resposta

Como o hexágono está inscrito na circunferência, seu lado coincide com o raio, que é de 10 cm.

O apótema é calculado da seguinte forma:

$reto alfa espaço igual a numerador reto r raiz quadrada de 3 sobre denominador 2 fim da fração reto alfa espaço igual a 10 numerador raiz quadrada de 3 sobre denominador 2 fim da fração reto alfa espaço igual a 5 raiz quadrada de 3 espaço$

Utilizando a fórmula que relaciona o perímetro e o apótema do hexágono, encontramos a sua área.

Calculando o perímetro, temos:

$reto P com reto h subscrito espaço igual a 6 espaço reto x espaço reto L reto P com reto h subscrito espaço igual a 6 espaço reto x espaço 10 espaço cm reto P com reto h subscrito espaço igual a 60 espaço cm$

Aplicamos o valor do perímetro e do apótema na fórmula.

$reto A com reto h subscrito espaço igual a espaço reto p sobre 2 reto x espaço reto alfa reto A com reto h subscrito espaço igual a 60 sobre 2 reto x espaço 5 raiz quadrada de 3 reto A com reto h subscrito espaço igual a 30 espaço reto x espaço 5 raiz quadrada de 3 reto A com reto h subscrito espaço igual a 150 raiz quadrada de 3$

Aprenda mais sobre o hexágono.

Confira como calcular a área de outras figuras planas:

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.