Área do Retângulo: como calcular, fórmula e exercícios

Rafael C. Asth

Professor de Matemática e Física

A área do retângulo corresponde ao produto (multiplicação) da medida da base pela altura da figura, sendo expressa pela fórmula:

A = b x h

Onde,
A: área
b: base
h: altura

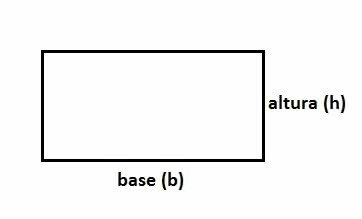
Área do Retângulo

Lembre-se que o retângulo é uma figura geométrica plana formada por quatro lados (quadrilátero). Dois lados do retângulo são menores e dois deles são maiores.

Ele possui quatro ângulos internos de 90° chamados de ângulos retos. Assim, a soma dos ângulos internos dos retângulos totalizam 360°.

Como calcular a área do retângulo?

Para calcular a superfície ou área do retângulo basta multiplicar o valor da base com o da altura.

Para exemplificar, vejamos abaixo um exemplo:

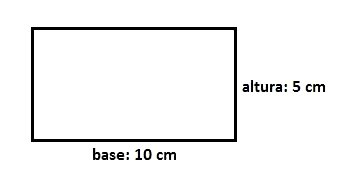
Aplicando-se a fórmula para calcular a área, num retângulo de base 10 cm e altura de 5 cm, temos:

$reto A espaço igual a espaço reto b espaço reto x espaço reto h reto A espaço igual a espaço 10 espaço cm espaço reto x espaço 5 espaço cm reto A espaço igual a espaço 50 espaço cm ao quadrado$

Portanto, o valor da área da figura é de 50 cm².

Perímetro do Retângulo

Não confunda a área com o perímetro, que corresponde a soma de todos os lados. No exemplo acima, o perímetro do retângulo seria de 30 cm. Ou seja: 10 + 10 + 5 + 5 = 30.

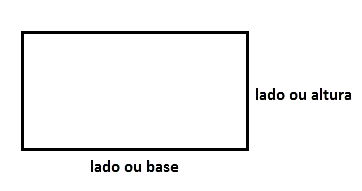
A fórmula para calcular o perímetro é:

P = 2 x (b + h)

Onde,

P: perímetro
b: base
h: altura

Aplicando-se a fórmula para calcular o perímetro do retângulo, de base 10 cm e altura 5 cm, temos:

$reto P espaço igual a espaço 2 espaço reto x espaço parêntese esquerdo reto b espaço mais espaço reto h parêntese direito reto P espaço igual a espaço 2 espaço reto x espaço parêntese esquerdo 10 espaço cm espaço mais espaço 5 espaço cm parêntese direito reto P igual a espaço 2 espaço reto x espaço 15 espaço cm reto P espaço igual a espaço 30 espaço cm$

Sendo assim, em um retângulo cuja base mede 10 cm e a altura é de 5 cm, o perímetro é 30 cm.

Veja também os artigos:

Diagonal do Retângulo

A linha que une dois vértices não consecutivos de um retângulo é chamada de diagonal. Assim, se traçarmos uma diagonal em um retângulo, percebemos que surgem dois triângulos retângulos.

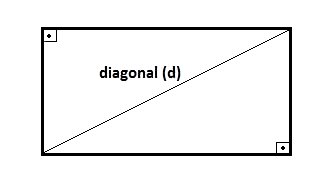
Dessa forma, o cálculo da diagonal do retângulo é feito através do Teorema de Pitágoras, onde o valor do quadrado da hipotenusa é igual a soma dos quadrados de seus catetos.

Logo, a fórmula para calcular a diagonal é expressa da seguinte maneira:

d²= b²+ h² ou d = $raiz quadrada de reto b ao quadrado mais reto h ao quadrado fim da raiz$

Onde,

d: diagonal
b: base
h: altura

Aplicando-se a fórmula para calcular a diagonal, num retângulo de base 10 cm e altura de 5 cm, temos:

$reto d ao quadrado igual a espaço reto b ao quadrado mais reto h à potência de 2 espaço fim do exponencial reto d ao quadrado igual a espaço parêntese esquerdo 10 espaço cm parêntese direito ao quadrado mais parêntese esquerdo 5 espaço cm parêntese direito à potência de 2 espaço fim do exponencial reto d ao quadrado espaço igual a espaço 100 espaço cm ao quadrado espaço mais espaço 25 espaço cm ao quadrado reto d ao quadrado espaço igual a espaço 125 espaço cm ao quadrado reto d espaço igual a espaço raiz quadrada de 125 espaço cm ao quadrado fim da raiz reto d espaço igual a espaço raiz quadrada de 5 ao quadrado espaço reto x espaço 5 fim da raiz espaço espaço espaço parêntese esquerdo pois espaço 5 espaço reto x espaço 5 espaço reto x espaço 5 igual a 5 ao quadrado espaço reto x espaço 5 igual a 125 parêntese direito reto d espaço igual a espaço 5 raiz quadrada de 5$

Logo, em um retângulo cuja base mede 10 cm e a altura é de 5 cm, a diagonal da figura é $5 raiz quadrada de 5$ .

Atenção!

Você deve observar as unidades de medidas dadas pelo exercício, visto que a base e a altura devem apresentar as mesmas unidades.

Por exemplo, se a unidade for dada em centímetros, a área será em centímetros quadrados (cm²), que corresponde a multiplicação entre as unidades de medida (cm x cm = cm²).

Da mesma maneira, se ela for dada em metros, a área será metros quadrados (m²).

Exercícios Resolvidos

Para fixar melhor o conhecimento, confira abaixo dois exercícios resolvidos sobre a área do retângulo:

Questão 1

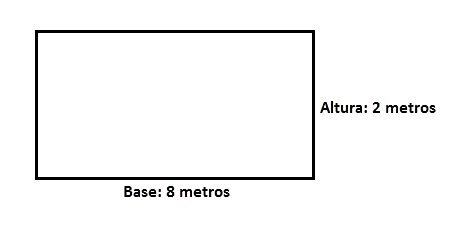
Calcule a área de um retângulo com base de 8 m e altura de 2 m.

Ver Resposta

Resposta correta: 16 m².

Nesse exercício, basta aplicar a fórmula da área:

$reto A igual a reto b espaço reto x espaço reto h espaço reto A igual a 8 espaço reto m espaço reto x espaço 2 espaço reto m reto A igual a 16 espaço reto m ao quadrado$

Questão 2

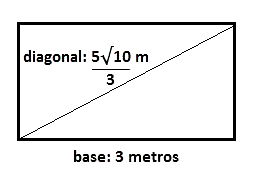
Calcule a área de um retângulo que apresenta uma base de 3 m e diagonal de $numerador 5 raiz quadrada de 10 sobre denominador 3 fim da fração$ m:

Ver Resposta

Resposta correta: A = 13 m².

Para resolver esse problema, primeiramente temos que encontrar o valor da altura do retângulo. Ela pode ser encontrada pela fórmula da diagonal:

$reto d ao quadrado igual a espaço reto b ao quadrado espaço mais reto h ao quadrado abre parênteses numerador 5 raiz quadrada de 10 sobre denominador 3 fim da fração fecha parênteses ao quadrado igual a 3 ao quadrado espaço mais espaço reto h ao quadrado numerador 5 raiz quadrada de 10 sobre denominador 3 fim da fração reto x espaço numerador 5 raiz quadrada de 10 sobre denominador 3 fim da fração igual a 9 espaço mais espaço reto h ao quadrado numerador espaço 5 espaço reto x espaço 5 raiz quadrada de 10 espaço reto x espaço 10 fim da raiz sobre denominador 3 espaço reto x espaço 3 fim da fração igual a espaço 9 espaço mais espaço reto h ao quadrado numerador espaço 25 raiz quadrada de 100 sobre denominador 9 fim da fração igual a espaço 9 espaço mais espaço reto h ao quadrado numerador espaço 25 espaço reto x espaço 10 sobre denominador 9 fim da fração igual a espaço 9 espaço mais espaço reto h ao quadrado numerador espaço 250 sobre denominador 9 fim da fração igual a espaço 9 espaço mais espaço reto h ao quadrado 250 espaço igual a espaço 81 espaço mais espaço 9 reto h ao quadrado 250 espaço menos espaço 81 espaço igual a 9 reto h ao quadrado 169 espaço igual a espaço 9 reto h ao quadrado reto h ao quadrado espaço igual a espaço 169 sobre 9 reto h espaço igual a espaço raiz quadrada de 169 sobre 9 fim da raiz reto h espaço igual a espaço 13 sobre 3$

Depois de encontrado o valor da altura, utilizamos a fórmula da área:

$reto A igual a espaço reto b espaço reto x espaço reto h reto A espaço igual a espaço 3 espaço reto m espaço reto x espaço 13 sobre 3 espaço reto m reto A espaço igual a espaço 13 espaço reto m ao quadrado$

Portanto, a área de um retângulo é 13 metros quadrado.

Questão 3

Observe o retângulo a seguir e escreva o polinômio que representa a área da figura. A seguir, calcule o valor da área quando x = 4.

$espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço em moldura de caixa fecha moldura espaço reto x espaço mais espaço 1 espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço 2 reto x espaço menos espaço 3$

Ver Resposta

Resposta correta: A = 2x²- x - 3 e A_{(x = 4)} = 25.

Primeiramente, substituímos os dados da imagem na fórmula da área do retângulo.

$reto A espaço igual a espaço reto b espaço reto x espaço reto h reto A espaço igual a espaço parêntese esquerdo 2 reto x espaço menos espaço 3 parêntese direito parêntese esquerdo reto x espaço mais espaço 1 parêntese direito$

Para encontrar o polinômio que representa a área devemos multiplicar termo a termo. Na multiplicação de letras iguais, repete-se a letra e soma-se os expoentes.

$reto A espaço igual a espaço parêntese esquerdo 2 reto x espaço menos espaço 3 parêntese direito parêntese esquerdo reto x espaço mais espaço 1 parêntese direito reto A espaço igual a espaço 2 reto x. reto x espaço mais espaço 2 reto x.1 espaço menos 3. reto x espaço menos espaço 3.1 reto A espaço igual a espaço 2 reto x ao quadrado espaço mais espaço 2 reto x espaço menos espaço 3 reto x espaço menos espaço 3 reto A espaço estreito igual a espaço 2 reto x ao quadrado menos espaço reto x espaço menos espaço 3$

Sendo assim, o polinômio que representa a área é 2x²- x - 3.

Agora, substituímos o valor de x por 4 e calculamos a área.

$reto A espaço estreito igual a espaço 2 reto x ao quadrado menos espaço reto x espaço menos espaço 3 reto A espaço igual a espaço estreito 2. parêntese esquerdo 4 parêntese direito ao quadrado espaço menos espaço 4 espaço menos espaço 3 reto A espaço igual a espaço 2.16 espaço menos espaço 7 reto A espaço igual a espaço 32 espaço menos espaço 7 reto A espaço igual a espaço 25$

Logo, quando temos x = 4, a área é 25 unidades.

Confira a área de outras figuras:

Pratique exercícios sobre área e perímetro.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações