Perímetro do Quadrado

Rafael C. Asth
Rafael C. Asth
Professor de Matemática e Física

O perímetro do quadrado corresponde a soma dos quatro lados dessa figura plana.

Lembre-se que o quadrado é um quadrilátero regular que apresenta lados com as mesmas medidas (congruentes). Assim, essa figura é composta por quatro ângulos retos (90°).

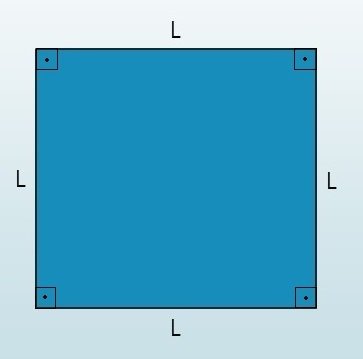
Perímetro do Quadrado

Cálculo do perímetro do quadrado

O perímetro do quadrado é calculado utilizando a fórmula:

começar estilo tamanho matemático 18px reto P igual a reto L espaço mais espaço reto L espaço mais espaço reto L espaço mais espaço reto L fim do estilo

ou

começar estilo tamanho matemático 18px reto P espaço igual a espaço 4 espaço. espaço reto L fim do estilo

Onde,
P é o perímetro,
L é a medida do lado do quadrado

Exemplo
Um quadrado possui lado igual a 4 m. Calcule seu perímetro.

P = 4 + 4 + 4 + 4 = 16 m

Saiba como calcular o Perímetro do Retângulo.

Fórmula da Área do quadrado

Diferente do perímetro, a área é a medida da superfície da figura. Assim, a área do quadrado é calculada pela fórmula:

reto A igual a reto L ao quadrado

Que tal saber mais sobre o tema? Leia Área e Perímetro.

Fique Atento!

A unidade de medida da área será sempre dada em cm2 ou m2.Isso porque ao multiplicar centímetro por centímetro (cm x cm) ou metro por metro (m x m), temos a medida elevada ao quadrado.

Note que no perímetro a unidade é centímetro (cm) ou metro (m), visto que é realizada uma soma e não uma multiplicação.

Diagonal do Quadrado

Ao passar uma linha entre uma extremidade e outra do quadrado ela forma dois triângulos retângulos, os quais apresentam um ângulo de 90°. Essa linha que corta a figura em duas metades é chamada diagonal.

reto d espaço igual a espaço reto L √ 2

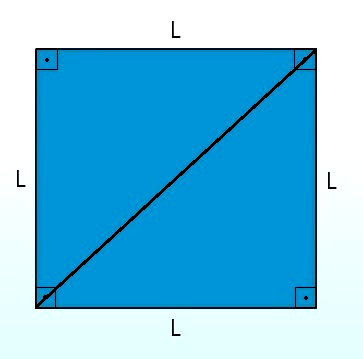
Perímetro do Quadrado

Para calcular a diagonal do quadrado utiliza-se o Teorema de Pitágoras.

Logo,

d2 = L2 + L2
d2 = 2L2
d = √2L2
d = L√2

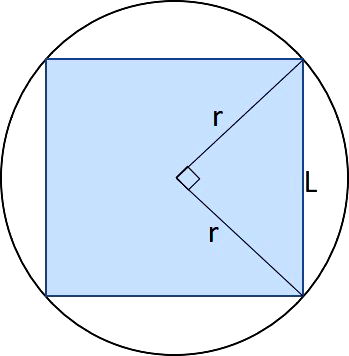
Quadrado Inscrito na circunferência

Quando um quadrado surge dentro de um círculo ele é chamado “quadrado inscrito”. Esse tipo de figura é muito comum aparecer em provas, vestibulares e concursos.

Para calcular as medidas dessa figura basta usar o Teorema de Pitágoras, em que r é o raio da circunferência e L o lado do quadrado.

r ao quadrado espaço mais espaço r ao quadrado igual a L ao quadrado 2 r ao quadrado espaço igual a espaço L ao quadrado raiz quadrada de 2 r ao quadrado fim da raiz igual a L ao quadrado r raiz quadrada de 2 espaço igual a espaço L

Quadrado inscrito na circunferência

Exercícios sobre perímetro do quadrado resolvidos

Exercício 1

Calcule o perímetro dos quadrados:

a) Um quadrado com 900 cm2 de área.

Primeiramente, vamos usar a fórmula da área para descobrir o valor dos lados desse quadrado.

A = L2
900 = L2
L = √900
L = 30 cm

Se o lado desse quadrado mede 30 cm, para encontrar o perímetro, basta somar esse valor quatro vezes:

P = 30 + 30 + 30 + 30
P = 120 cm

b) Um quadrado com lados de 70 m.

P = 4L
P = 4.70
P = 280 m

c) Um quadrado com diagonal de 4√2cm.

d = L√2
4√2= L√2
L = 4√2/√2
L = 4 cm

Agora, basta colocar na fórmula do perímetro:

P = 4L
P = 4.4
P = 16 cm

Exercício 2

Determine o valor do perímetro de um quadrado inscrito numa circunferência de raio 10 cm.

L = r√2
L = 10√2

Agora, basta colocar o valor do lado do quadrado na fórmula do perímetro:

P = 4L
P = 4.10√2
P = 40√2

Curiosidade

O quadrado é considerado um tipo de retângulo especial. No entanto, um retângulo não pode ser considerado um quadrado.

Saiba mais sobre outras figuras geométricas nos artigos:

Rafael C. Asth
Rafael C. Asth
Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.
Veja também