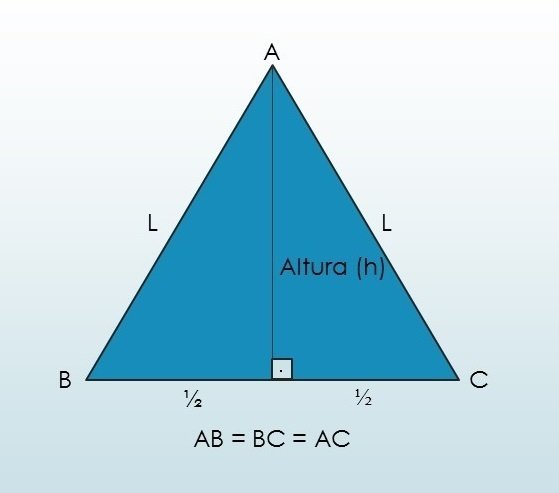
Triângulo Equilátero

Rafael C. Asth

Professor de Matemática e Física

O triângulo equilátero é um tipo de triângulo que possui os três lados congruentes (mesma medida).

Além dos lados, os ângulos internos dessa figura apresentam as mesmas medidas: 3 ângulos de 60º, os quais totalizam 180°.

Lembre-se que os triângulos são figuras planas e fechadas constituídas por segmentos de reta, as quais são chamadas de polígonos.

Área do Triângulo Equilátero

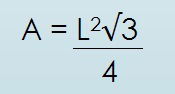
A: área
L: lado

Veja mais sobre área de figuras planas.

Perímetro do Triângulo Equilátero

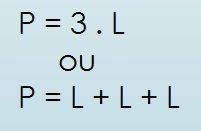
P: perímetro
L: lado

Veja mais sobre Perímetros de Figuras Planas.

Altura do Triângulo Equilátero

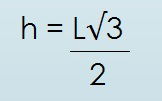
h: altura
L: lado

Fique Atento!
Lembre-se que a soma dos ângulos internos de qualquer triângulo totaliza 180°. Já a soma dos ângulos externos sempre resulta em 360º.

Tipos de Triângulos

Além do triângulo equilátero existem outros tipos de triângulos:

Em relação aos lados:

Triângulo Isósceles: apresenta dois lados iguais e um diferente. Dois ângulos internos são congruentes.
Triângulo Escaleno: os três lados e os ângulos internos são diferentes.

Em relação aos ângulos internos:

Triângulo Retângulo: formado por um ângulo interno reto (90°).
Triângulo Obtusângulo: formado por dois ângulos internos agudos (menor que 90°) e um ângulo interno obtuso (maior que 90°).
Triângulo Acutângulo: formado por três ângulos internos menores que 90°.

Saiba mais sobre semelhança de triângulos.

Exercícios sobre triângulo equilátero

Exercício 1

Calcule a área de um triângulo equilátero com lado de 6 cm.

Exercício 2

Calcule o Perímetro de um triângulo equilátero que apresenta lados de 12 cm de lado.

Aprenda mais com:

Triângulo: tudo sobre este polígono

Rafael C. Asth

Professor de Matemática, licenciado e pós-graduado em ensino da Matemática e da Física. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.