Triângulo: tudo sobre este polígono
Triângulo é um polígono com três ângulos, lados e vértices, que pertencem ao mesmo plano. Este polígono, sempre convexo, é a junção dos três segmentos de reta não colineares que, em pares, formam os três ângulos e delimitam sua região interna.
Esta figura é largamente utilizada com diversas aplicações. Na engenharia, por ser um elemento rígido, que não se deforma, concede estabilidade às estruturas.
Entre todos, este é o único polígono que não possui diagonal, além de se apresentar em vários formatos. São classificados quanto as características de comprimento dos lados e medidas de seus ângulos.
Tipos de triângulos
Os triângulos podem ser classificados quanto aos lados e ângulos, havendo três tipos principais para cada.
Obtusângulo, retângulo e acutângulo
Em relação aos ângulos, os triângulos são classificados tendo como parâmetro o ângulo de 90º.
Obtusângulo
O triângulo obtusângulo possui um ângulo obtuso, ou seja, maior que 90º. Isto faz com que os outros dois sejam menores que 90º.

Retângulo
O triângulo retângulo é aquele que, como sugere seu nome, possui um ângulo reto, de 90º.

Acutângulo
O triângulo acutângulo é o que possui os três ângulos menores que 90º.

Além dos tipos de triângulos em relação aos ângulos, o comprimento dos lados também os classifica em três categorias.
Equilátero, isósceles e escaleno
Em relação aos lados, os critérios para classificar os triângulos são seus comprimentos, sendo: os três iguais, apenas dois iguais ou, nenhum igual.
Equilátero
O triângulo equilátero possui os três lados de mesma medida, o que o leva a possuir os três ângulos internos também iguais, com 60º.
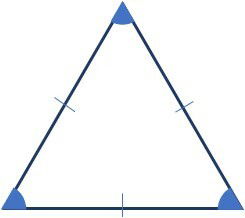
Isósceles
O triângulo isósceles possui dois lados com mesmo comprimento e, devido a isto, dos dois ângulos referentes à base, também são iguais.

Escaleno
O triângulo escaleno possui os três lados com medidas diferentes e, por consequência, três ângulos com medidas diferentes.

Aprenda mais sobre classificação dos triângulos.
Área do triângulo
A medida da área, região interna, delimitada pelos três lados de um triângulo, pode ser calcula de algumas formas. Cada uma oferece suas vantagens de cálculo, dependendo das informações disponíveis.
Um modo muito utilizado é o que depende da medida da base e da altura.
Onde,
A é a área,
b é a medida da base,
h é a medida da altura.
Fórmula de Heron da área do triângulo
Também é possível calcular a área de um triângulo com a fórmula de Heron, que se utiliza das medidas dos três lados e não depende da altura.
Onde,
p é o semiperímetro, isto é, a metade do perímetro, calculado como:
Onde a, b e c são as medidas dos lados.
Veja mais sobre área do triângulo.
Perímetro do triângulo
O perímetro é a soma das medidas dos lados de qualquer polígono. Como o triângulo possui três lados:
Onde a, b e c são as medidas dos lados.
Aprenda mais sobre perímetro do triângulo.
Condição de existência de um triângulo
Para que um triângulo exista, é necessário seus lados se encontrarem nos vértices. No entanto, nem todo trio de segmentos satisfaz esta condição.
Para que um triângulo possa ser formado, deve a medida de cada lado ser inferior a soma dos outros dois.
Considerando um triângulo qualquer, de lados a, b e c, para que este triângulo possa ser construído, deve-se satisfazer:
Altura, mediatriz, mediana e bissetriz
Estes quatro elementos geométricos são extremamente importantes no estudo dos triângulos. Eles conferem características e propriedades aos triângulos. Como todos se referem a lados e ângulos, todo triângulo terá três dos seguintes elementos:
Altura
A altura é um segmento de reta que liga um vértice ao lado oposto, formando um ângulo de 90º com o lado que intercepta, ou seu prolongamento.

A altura de um triângulo pode estar em seu interior ou exterior. Como há três lados, haverão três alturas, uma relativa a cada lado.
Mediatriz
A mediatriz é uma reta que corta o ponto médio de um lado do triângulo, formando um ângulo de 90º.
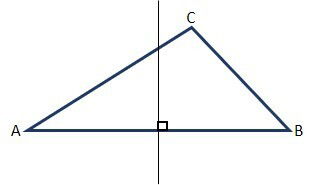
A mediatriz em relação ao lado AB, o intercepta no seu ponto médio, ou seja, ao meio, formando um ângulo de 90º com este lado.
Veja mais de mediatriz.
Mediana
A mediana é um segmento que liga um vértice ao ponto médio do lado oposto.
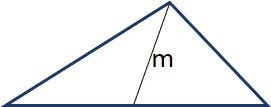
Embora a mediana também divida o lado oposto ao ângulo em duas partes iguais, diferente da mediatriz, ela não faz um ângulo de 90º com o lado.
Bissetriz
A bissetriz é uma semirreta que divide um ângulo ao meio.
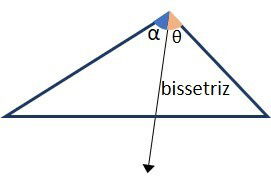
Como a bissetriz divide um ângulo em dois iguais, temos que .
Pontos notáveis de um triângulo
Em um triângulo há quatro pontos notáveis, formados pelas intersecções entre as três alturas, mediatrizes, bissetrizes, e medianas. Estes pontos, podem ser internos ou externos aos triângulos e lhe conferem características e propriedades.
Ortocentro
O ortocentro é o ponto de intersecção entre as três alturas.
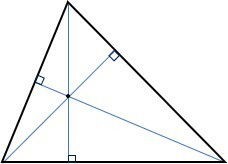
O ortocentro pode ser interno, externo ou pertencer ao triângulo. Interno se o triângulo é acutângulo, externo se é obtusângulo e pertencer ao triângulo se for um triângulo retângulo.
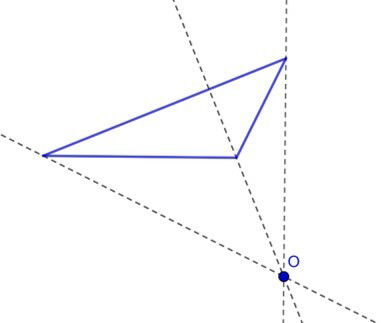
Circuncentro
É o ponto de encontro das três mediatrizes.
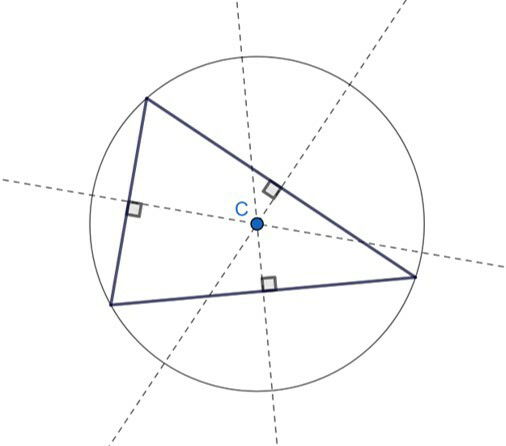
O circuncentro é o centro da circunferência circunscrita ao triângulo.
Incentro
É o ponto de encontro das bissetrizes.
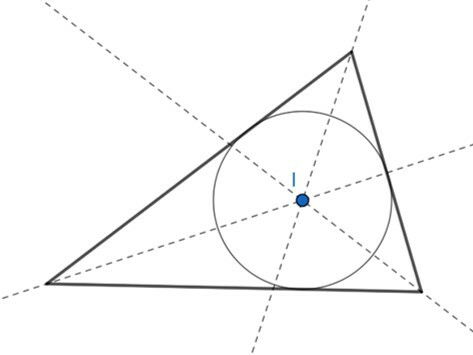
O incentro é o centro da circunferência inscrita ao triângulo.
Baricentro
É o ponto de intersecção entre as medianas.
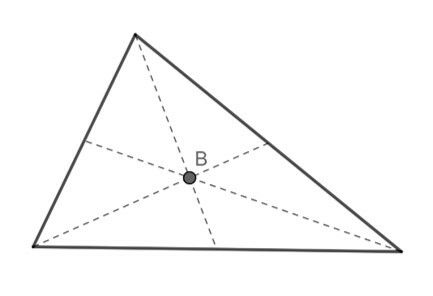
O baricentro é o centro de massa ou, de gravidade, do triângulo.
Ângulos internos e externos do triângulo
Em um triângulo, a soma dos três ângulos internos é igual a 180º.
Onde,
são os ângulos internos do triângulo.
Ângulo externo
Um ângulo externo é formado entre o prolongamento de um dos lados, e o lado adjacente. Todo ângulo externo é suplementar ao interno, ao seja, ambos somados são iguais a 180º.
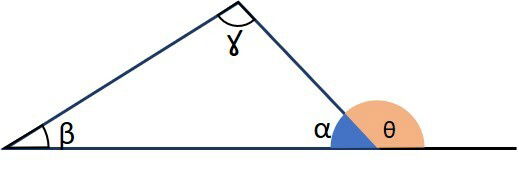
Na imagem, é um ângulo externo, suplementar ao ângulo interno, ou seja,
.
Teorema do ângulo externo
O teorema do ângulo externo diz que a medida de um ângulo externo, é igual a soma dos outros dois ângulos internos.
Em relação ao ângulo destacado na figura, temos:
Triângulo inscrito e circunscrito a circunferência
Um triângulo inscrito a uma circunferência é interior a ela e, seus vértices ficam sobre a linha da circunferência.
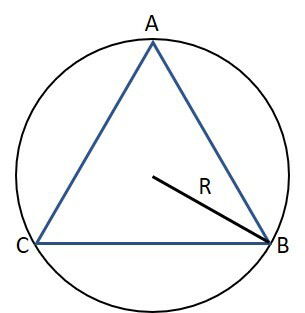
Os pontos dos vértices A, B e C também pertencem à circunferência.
No triângulo equilátero inscrito na circunferência, a medida do lado se relaciona com o raio da circunferência, como:
Onde L é a medida do lado e R a do raio.
Um triângulo circunscrito a uma circunferência é exterior a ela e, a circunferência tangencia os lados do triângulo.
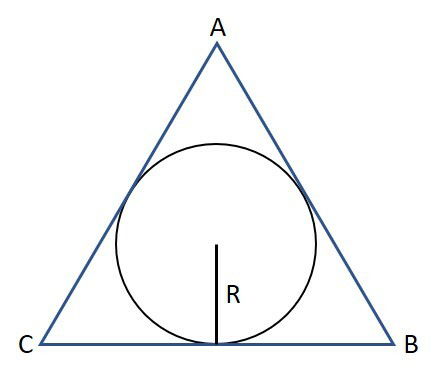
Um triângulo equilátero circunscrito a uma circunferência se relaciona com seu raio, por:
Onde L é a medida do lado e R a do raio.
Veja também:
- Exercícios sobre triângulos explicados
- Soma dos ângulos internos de um triângulo
- Triângulo Retângulo
- Triângulo Equilátero
- Triângulo Escaleno
- Triângulo Isósceles
- Semelhança de Triângulos
- Semelhança de Triângulos - Exercícios
- Teorema de Pitágoras
ASTH, Rafael. Triângulo: tudo sobre este polígono. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/triangulo/. Acesso em:



